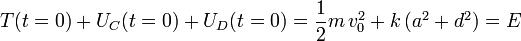Partícula sometida a la acción de dos muelles (GIA)
De Laplace
Contenido |
1 Enunciado
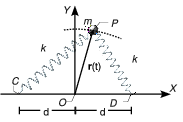
Una partícula P, de masa m, se mueve en el plano horizontal sometida a la acción de dos resortes elásticos ideales e idénticos, de constante k y longitud natural nula. Los puntos de anclaje son C( − d,0) y D(d,0), respectivamente
- Escribe la ecuación diferencial que determina el movimiento de la partícula.
- Si las condiciones iniciales son
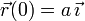 y
y 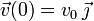 , encuentra las expresiones que dan la posición y la velocidad de la partícula en todo instante de tiempo.
, encuentra las expresiones que dan la posición y la velocidad de la partícula en todo instante de tiempo.
- Determina, para todo instante de tiempo, el momento cinético,
 , de la partícula P respecto al origen de coordenadas O, así como su energía mecánica, E. ¿Qué teoremas de conservación explican las propiedades de estas magnitudes en este problema?
, de la partícula P respecto al origen de coordenadas O, así como su energía mecánica, E. ¿Qué teoremas de conservación explican las propiedades de estas magnitudes en este problema?
2 Solución
2.1 Ecuación del movimiento
La expresión que da la ecuación del movimiento es la Segunda Ley de Newton
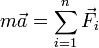
donde, m es la masa de la partícula,  su aceleración respecto de un sistema
inercial y
su aceleración respecto de un sistema
inercial y 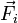 las fuerzas que actúan sobre ella.
las fuerzas que actúan sobre ella.
Usamos coordenadas cartesianas y el sistema de ejes de la figura. Al ser un movimiento plano podemos ignorar la componente de los vectores en el eje OZ. El vector de posición, la velocidad y la aceleración de la partícula son
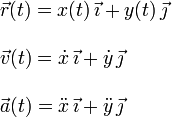
En este problema, considerando que el movimiento se desarrolla sobre un plano, la
partícula está sometida a dos fuerzas, la de cada uno de los muelles. (Si hiciéramos el
experimento sobre una mesa, el peso de la partícula se vería compensado en cada instante
por la f.r.v. de la mesa, con lo que no afectan al movimiento). Como son dos resortes
ideales, si el vector de posición de la partícula es 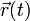 , la fuerza que ejerce
sobre ella cada uno de los muelles es
, la fuerza que ejerce
sobre ella cada uno de los muelles es

Los vectores 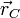 y
y 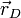 son los vectores de posición de los puntos de
anclaje de los muelles. Si escogemos el sistema de ejes de la figura estos vectores son
son los vectores de posición de los puntos de
anclaje de los muelles. Si escogemos el sistema de ejes de la figura estos vectores son

En la coordenadas cartesianas que hemos elegido la expresión de las fuerzas es
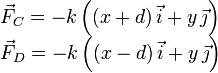
Podemos escribir la ecuación del movimiento.
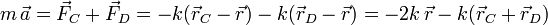
Como podemos ver en la figura y en la expresión de los vectores, se cumple
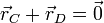 . La ecuación se puede escribir
. La ecuación se puede escribir
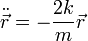
Esto es la ecuación de un movimiento armónico. La podemos escribir como

La solución general es una superposición de senos y cosenos. Lo único nuevo en esta ecuación es que los coeficientes de la combinación lineal son vectores en vez de escalares. Es decir, la solución es de la forma
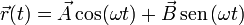
y la velocidad se obtiene derivando respecto al tiempo

2.2 Solución concreta
El enunciado nos da las condiciones iniciales

Para aplicarlas evaluamos en t = 0 las expresiones de 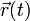 y
y 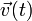 obtenidas en el apartado anterior
obtenidas en el apartado anterior
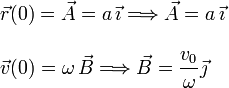
Las expresiones de la posición y la velocidad en cada instante son
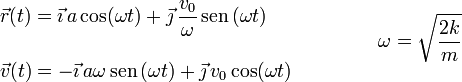
2.3 Momento cinético
El momento cinético respecto al origen en cada instante es
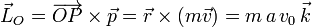
Vemos que no depende del tiempo. Eso se debe a que la fuerza resultante sobre la partícula es central respecto al punto O. Entonces
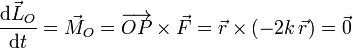
2.4 Energía cinética
La energía cinética es

No permanece constante pues la velocidad de la partícula cambia con el tiempo.
Por otro lado, la energía potencial asociada a los muelles es
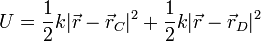
Tenemos
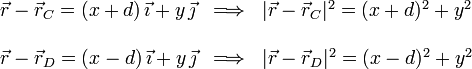
Entonces
![U = \dfrac{k}{2}\left( |\vec{r}-\vec{r}_C|^2 + |\vec{r}-\vec{r}_D|^2\right) =
k(x^2+y^2) + kd^2=
k\left[ a^2\cos^2(\omega t) + \dfrac{v_0^2}{\omega^2}\,\mathrm{sen}\,^2(\omega t) \right] + kd^2](/wiki/images/math/c/c/2/cc29625b34f2be4f0aa10c02bc1aa4dc.png)
Tampoco es constante pues la elongación de los muelles cambia en el tiempo.
La energía mecánica es la suma de la cinética y la potencial
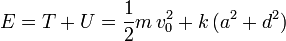
La energía mecánica si es constante en el tiempo, pues no hay fuerzas no conservativas actuando sobre la partícula. Podríamos haber calculado el valor de la energía mecánica a partir de las condiciones iniciales
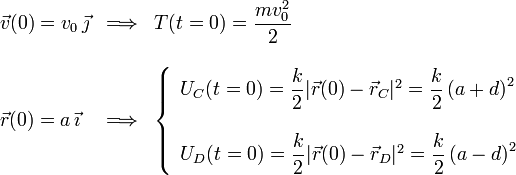
Sumando obtenemos