De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

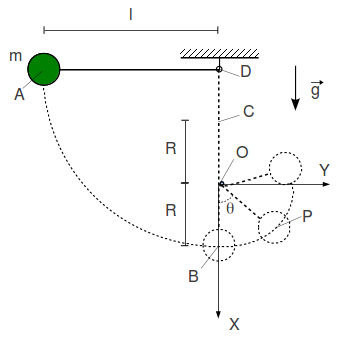
Un péndulo consiste en una pequeña masa $m$ atada al extremo de una cuerda inextensible y sin masa de longitud $l$ . La masa se coloca en el plano horizontal y se suelta. En el punto más bajo de la oscilación (punto $B$ ), la cuerda choca con una clavija delgada (punto $O$ ) situada a una distancia $R$ por encima de del punto $B$ .

Para el punto más bajo de la oscilación (punto $B$ ) calcula el módulo de la velocidad de la masa, su cantidad de movimiento y su momento cinético respecto al punto $D$ .
Expresa en coordenadas polares la posición respecto del punto $O$ de la masa después de que la cuerda haya chocado con la clavija (punto $P$ ). Encuentra la expresión de la velocidad y la aceleración de la masa.
Para el movimiento de la masa después del punto $B$ , encuentra la expresión de la ecuación diferencial que rige la variación del ángulo $θ$ , la expresión que da la tensión de la cuerda y las condiciones iniciales de la ecuación diferencial en el punto $B$ .
¿Cuál es la condición que debe cumplir la distancia $R$ para que la masa describa al menos un círculo completo alrededor de la clavija, es decir, para que llegue al punto $C$ ?

2 Solución

2.1 Velocidad, cantidad de movimiento y momento cinético en B

El movimiento de la masa no es un movimiento armónico simple. Para un péndulo esto sólo ocurre si el ángulo de oscilación es pequeño. En este caso no es así. Este apartado hay que resolverlo usando la conservación de la energía mecánica.

Durante su movimiento la masa está sometida la acción de dos fuerzas: el peso y la tensión de la cuerda. Está última no realiza trabajo, pues es siempre perpendicular a la velocidad. Como el peso es conservativo, se puede definir una energía potencia gravitatoria. La energía mecánica del sistema se conserva pues la tensión de la cuerda no realiza trabajo.

Escogemos como origen de energía potencial gravitatoria la altura correspondiente al punto A

$U_{g}^A = 0$

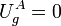
Como la masa parte del reposo, su energía cinética en A es cero. Entonces la energía mecánica es

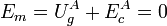
$E_m = U_{g}^A + E_c^A = 0$

Cuando llega a B, su energía potencial gravitatoria es

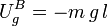
$U_g^B = -m\,g\,l$

y su energía cinética es

$E_c^B = \dfrac{1}{2}\,m\,v_B^2$

La energía mecánica en B es

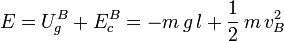
$E = U_g^B + E_c^B = -m\,g\,l + \dfrac{1}{2}\,m\,v_B^2$

Como la energía mecánica se conserva tenemos

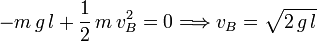
$-m\,g\,l + \dfrac{1}{2}\,m\,v_B^2 = 0 \Longrightarrow v_B = \sqrt{2\,g\,l}$

Este es el módulo de la velocidad en B. La dirección es horizontal y el sentido apuntando hacia la derecha. Usando los ejes indicados en la figura el vector velocidad es

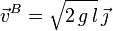
$\vec{v}^B = \sqrt{2\,g\,l}\,\vec{\jmath}$

La cantidad de movimiento en B es

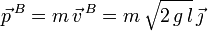
$\vec{p}^{\,B} = m\,\vec{v}^{\,B} = m\,\sqrt{2\,g\,l}\,\vec{\jmath}$

El momento cinético respecto al punto D es

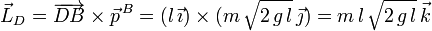
$\vec{L}_{D} = \overrightarrow{DB}\times\vec{p}^{\,B} = (l\,\vec{\imath})\times(m\,\sqrt{2\,g\,l}\,\vec{\jmath}) = m\,l\,\sqrt{2\,g\,l}\,\vec{k}$

2.2 Posición, velocidad y aceleración después de B

Cuando la masa llega al punto B, la cuerda choca con el clavo, y la cuerda se enrolla a su alrededor. El enunciado dice que la clavija es delgada, por lo que podemos despreciar su radio. Esto quiere decir que después del punto B la masa describe un movimiento circular de radio $R$ . Traducido a coordenadas polares quiere decir que la coordenada radial es constante e igual a $R$ . Por tanto

$\rho = R\qquad\qquad \dot{\rho}=0 \qquad\qquad \ddot{\rho}=0$

La posición del punto P en polares viene dada por el vector

$\vec{r}^P = \overrightarrow{OP} = R\,\vec{u}_{\rho}$

La velocidad se obtiene derivando respecto al tiempo. Usando que 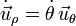$\dot{\vec{u}}_{\rho} = \dot{\theta}\,\vec{u}_{\theta}$ , tenemos que

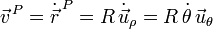
$\vec{v}^{\,P} = \dot{\vec{r}}^{\,P} = R\,\dot{\vec{u}}_{\rho} = R\,\dot{\theta}\,\vec{u}_{\theta}$

Para calcular la aceleración usamos que 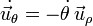$\dot{\vec{u}_{\theta}}=-\dot{\theta}\,\vec{u}_{\rho}$ . Tenemos

$\vec{a}^{\,P} = \dot{\vec{v}}^{\,P} = R\ddot{\theta}\,\vec{u}_{\theta} + R\,\dot{\theta}\,\dot{\vec{u}}_{\theta} = -R\,\dot{\theta}^2\,\vec{u}_{\rho} + R\,\ddot{\theta}\,\vec{u}_{\theta}$

2.3 Ecuación diferencial del ángulo y tensión de la cuerda

La ecuación diferencial se obtiene aplicando la Segunda Ley de Newton. Después del punto B, la masa sigue sometida a la acción de la cuerda y del peso. La Segunda Ley se escribe

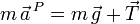
$m\,\vec{a}^{\,P} = m\,\vec{g} + \vec{T}$

Tenemos que expresar esos tres vectores en la base polar. Usando el apartado anterior tenemos

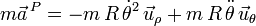
$m\vec{a}^{\,P} = -m\,R\,\dot{\theta}^2\,\vec{u}_{\rho} + m\,R\,\ddot{\theta}\,\vec{u}_{\theta}$

El vector $\vec{T}$ representa la tensión de la cuerda, y apunta siempre hacia el punto O.

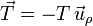
$\vec{T} = -T\,\vec{u}_{\rho}$

El peso es vertical apuntando hacia abajo. Tenemos

$m\,\vec{g} = m\,g\,\vec{\imath} = m\,g\cos\theta\,\vec{u}_{\rho} - m\,g\,\mathrm{sen}\,\theta\,\vec{u}_{\theta}$

Ahora podemos descomponer la Segunda Ley (ecuación vectorial) en dos ecuaciones escalares, igualando las componentes de 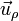$\vec{u}_{\rho}$ por un lado y de 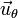$\vec{u}_{\theta}$ por el otro

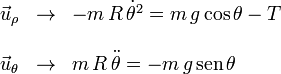
$\begin{array}{lcl} \vec{u}_{\rho} &\to& -m\,R\,\dot{\theta}^2 = m\,g\cos\theta - T\\ &&\\ \vec{u}_{\theta} &\to& m\,R\,\ddot{\theta} = -m\,g\,\mathrm{sen}\,\theta \end{array}$

La segunda ecuación es la ecuación diferencial del ángulo

$\ddot{\theta} = -\dfrac{g}{R}\,\mathrm{sen}\,\theta$

La segunda nos dice cuanto vale la tensión de la cuerda

$T = m\,(g\cos\theta + R\,\dot{\theta}^2)$

Las condiciones iniciales en B son que el ángulo $θ$ es cero y el módulo de la velocidad es $v_B=\sqrt{2\,g\,l}$ calculado en el primer apartado. Expresado en términos del ángulo queda

$\begin{array}{l} {\theta}(B) = 0\\ \\ \dot{\theta}(B) = \dfrac{v_B}{R} = \dfrac{\sqrt{2\,g\,l}}{R} \end{array}$

2.3.1 Condición para que llegue al punto C

Para que la masa llegue al punto C, debe realizar un movimiento circular de radio $R$ . Pero para que eso ocurra la cuerda tiene que estar tensa durante el movimiento de la masa entre los puntos B y C. Es decir, la tensión debe ser no nula. La condición límite ocurre cuando la tensión se anula en el instante en que la partícula llegue al punto C. Es decir,

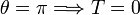
$\theta = \pi \Longrightarrow T = 0$

Imponiendo esa condición en la expresión de la tensión del apartado anterior obtenemos el valor mínimo que debe tener $\dot{\theta}$ en el punto C

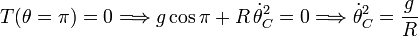
$T(\theta=\pi)=0 \Longrightarrow g\cos\pi + R\,\dot{\theta}_C^2=0 \Longrightarrow \dot{\theta}_C^2 = \dfrac{g}{R}$

Ahora bien, $\dot{\theta}$ se relaciona con la velocidad de la partícula. Como se ve en el apartado 2, el módulo de la velocidad es

$v_C = R\dot{\theta}_C \Longrightarrow \dot{\theta}_C = v_C/R$

Por tanto, para que llegue a C, la velocidad de la masa en ese punto debe ser

$v_C^2 = g\,R$

Por otro lado, la energía mecánica se conserva durante todo el movimiento, desde el punto A hasta el C (la tensión de la cuerda nunca realiza trabajo). La energía mecánica en C sería la suma de las energías potencial y cinética en C, y debe ser igual a cero, que es la energía mecánica original en A

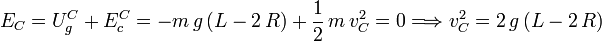
$E_C = U_{g}^C + E_c^C = -m\,g\,(L-2\,R) + \dfrac{1}{2}\,m\,v_C^2=0 \Longrightarrow v_C^2 = 2\,g\,(L-2\,R)$

Sustituyendo la condición para la velocidad mínima en C tenemos

$2\,g\,(L-2\,R) \geq g\,R \Longrightarrow R\leq\dfrac{2}{5}\,L$

2.3.1.1 Forma alternativa de encontrar la velocidad mínima en C

La condición sobre la velocidad mínima de la masa en el punto C puede encontrarse sin resolver los dos apartados anteriores. Como hemos dicho, para que la masa llegue al punto C es necesario que la cuerda se mantenga tensa, para que el movimiento de la masa sea circular. En el caso límite, la tensión de la cuerda en el punto C debe ser nula. Si eso ocurre, en el instante en el que la masa está en el punto C la única fuerza que actúa sobre ella es la gravedad, que es perpendicular a la trayectoria para ese instante. Entonces, la aceleración normal de la masa debe ser igual a la gravedad en el punto C. Tenemos

$a_n^C = g \Longrightarrow \dfrac{v_C^2}{R}=g \Longrightarrow v_C^2 = g\,R$

Reobtenemos la condición sobre la velocidad. Esta es la velocidad mínima. Si es mayor que este valor la tensión cuando la masa está en el punto C es mayor que cero, pero si es menor tendríamos una tensión negativa, lo que no tiene sentido.

2.3.2 Errores comunes

Comentamos aquí los errores comunes encontrados durante la corrección del problema

El movimiento del péndulo no es armónico simple. Eso sólo ocurre en un péndulo en el cual el ángulo de oscilación es pequeño, lo que no es el caso aquí.
El momento cinético es el momento de la cantidad de movimiento, no de una fuerza. Y desde luego no es la energía cinética de la masa.
Al encontrar la expresiones en polares, hay que usar el hecho de que la partícula recorre una circunferencia de radio $R$ constante. Por tanto la coordenada radial es constante y sus derivadas son nulas: $\rho=R,\quad \dot{\rho}=0,\quad \ddot{\rho}=0$ .
La condición para que la masa llegue al punto C no es que $R < L / 2$ . Eso sólo garantiza que la masa no choca con el techo si llegara a girar.
La condición tampoco es que la velocidad en C sea cero. El movimiento de la masa tiene que ser una circunferencia, por lo que tiene que haber una aceleración normal y, por tanto, un módulo de velocidad distinto de cero.

Péndulo enrollándose alrededor de una clavija delgada, Enero 2012 (G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Velocidad, cantidad de movimiento y momento cinético en B

2.2 Posición, velocidad y aceleración después de B

2.3 Ecuación diferencial del ángulo y tensión de la cuerda

2.3.1 Condición para que llegue al punto C

2.3.1.1 Forma alternativa de encontrar la velocidad mínima en C

2.3.2 Errores comunes

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES