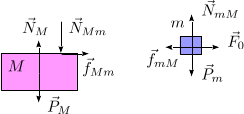De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

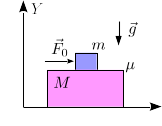
Un bloque de masa $m$ puede deslizar sobre otro bloque de masa $M = 2 m$ . El contacto entre los dos bloques es rugoso con coeficiente de rozamiento estático $μ$ . El bloque de masa $M$ desliza sin rozamiento sobre una superficie horizontal. Se aplica sobre el bloque superior una fuerza horizontal 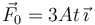$\vec{F}_0 = 3At\,\vec{\imath}$ , con $A > 0$ y constante y $t$ el tiempo.

Si la masa superior no desliza respecto de la inferior, ¿cuál es la aceleración de las masas?
¿En que instante la masa superior empieza a deslizar respecto a la inferior?
Supongamos ahora que hay rozamiento entre el bloque inferior y la superficie horizontal, con un coeficiente de rozamiento dinámico $μ$ . ¿Cuánto vale la aceleración de los bloques en este caso?
¿En que instante empieza a deslizar el bloque superior respecto del inferior en este caso?

2 Solución

2.1 Aceleración de las masas

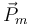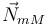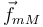El dibujo de la derecha muestra el diagrama de cuerpo libre de las dos masas. Las fuerzas sobre la masa $m$ son su peso, $\vec{P}_m$ , la fuerza $\vec{F}_0$ , la fuerza vincular ejercida por la masa inferior, $\vec{N}_{mM}$ y la fuerza de rozamiento también ejercida por la masa inferior, $\vec{f}_{mM}$ .

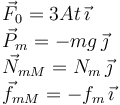
$\begin{array}{l} \vec{F}_0 = 3At\,\vec{\imath}\\ \vec{P}_m = -mg\,\vec{\jmath}\\ \vec{N}_{mM} = N_{m}\,\vec{\jmath}\\ \vec{f}_{mM} = -f_{m}\,\vec{\imath} \end{array}$

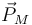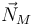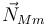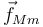Para la masa $M$ las fuerzas son su peso, $\vec{P}_M$ , la fuerza vincular ejercida por el suelo, $\vec{N}_{M}$ , la fuerza vincular ejercida por la masa superior, $\vec{N}_{Mm}$ y la fuerza de rozamiento también ejercida por la masa superior, $\vec{f}_{Mm}$ .

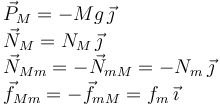
$\begin{array}{l} \vec{P}_M = -Mg\,\vec{\jmath}\\ \vec{N}_{M} = N_{M}\,\vec{\jmath}\\ \vec{N}_{Mm} = -\vec{N}_{mM} = -N_{m}\,\vec{\jmath}\\ \vec{f}_{Mm}= -\vec{f}_{mM} = f_{m}\,\vec{\imath} \end{array}$

Aplicamos la Segunda Ley de Newton a cada masa, teniendo en cuenta que su aceleración es la misma

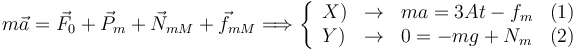
$m\vec{a} = \vec{F}_0 + \vec{P}_m + \vec{N}_{mM} + \vec{f}_{mM} \Longrightarrow \left\{ \begin{array}{lclr} X) & \to & ma = 3At - f_m & (1)\\ Y) & \to & 0 = -mg + N_m & (2) \end{array} \right.$

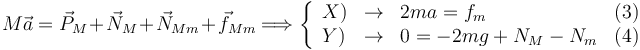
$M\vec{a} = \vec{P}_M + \vec{N}_M + \vec{N}_{Mm} + \vec{f}_{Mm} \Longrightarrow \left\{ \begin{array}{lclr} X) & \to & 2ma = f_m & (3)\\ Y) & \to & 0 = -2mg + N_M - N_m & (4) \end{array} \right.$

Sumando las ecuaciones (1) y (3) obtenemos

$\vec{a} = \dfrac{At}{m}\,\vec{\imath}$

2.2 Deslizamiento de la masa superior

De la ecuación (3) obtenemos

$\vec{f}_{mM} = 2At\,\vec{\imath}, \qquad \vec{N}_{mM} = mg\,\vec{\jmath}.$

La masa superior no desliza mientras que la fuerza de rozamiento sea capaz de impedirlo. Esto ocurre cuando la fuerza de rozamiento supera el valor máximo que puede alcanzar. Es decir

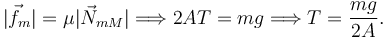
$|\vec{f}_m| = \mu|\vec{N}_{mM}| \Longrightarrow 2AT=mg \Longrightarrow T = \dfrac{mg}{2A}.$

2.3 Rozamiento de la masa inferior con el suelo

Lo único que cambia es que ahora hay que añadir una fuerza de rozamiento ejercida por el suelo sobre la masa inferior. Pero esta fuerza de rozamiento es en régimen dinámico, por lo que su módulo es igual al coeficiente de rozamiento dinámico multiplicado por el módulo de la fuerza normal del suelo sobre la masa inferior. Las fuerzas sobre la masa $m$ son

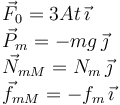
$\begin{array}{l} \vec{F}_0 = 3At\,\vec{\imath}\\ \vec{P}_m = -mg\,\vec{\jmath}\\ \vec{N}_{mM} = N_{m}\,\vec{\jmath}\\ \vec{f}_{mM} = -f_{m}\,\vec{\imath} \end{array}$

Y sobre la masa inferior

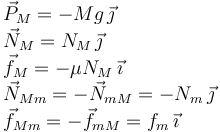
$\begin{array}{l} \vec{P}_M = -Mg\,\vec{\jmath}\\ \vec{N}_{M} = N_{M}\,\vec{\jmath}\\ \vec{f}_{M}= -\mu N_M\,\vec{\imath}\\ \vec{N}_{Mm} = -\vec{N}_{mM} = -N_{m}\,\vec{\jmath}\\ \vec{f}_{Mm}= -\vec{f}_{mM} = f_{m}\,\vec{\imath} \end{array}$

Aplicamos de nuevo la Segunda Ley a cada masa

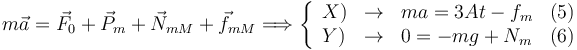
$m\vec{a} = \vec{F}_0 + \vec{P}_m + \vec{N}_{mM} + \vec{f}_{mM} \Longrightarrow \left\{ \begin{array}{lclr} X) & \to & ma = 3At - f_m & (5)\\ Y) & \to & 0 = -mg + N_m & (6) \end{array} \right.$

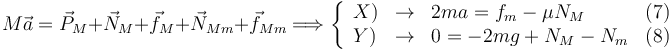
$M\vec{a} = \vec{P}_M + \vec{N}_M + \vec{f}_M + \vec{N}_{Mm} + \vec{f}_{Mm} \Longrightarrow \left\{ \begin{array}{lclr} X) & \to & 2ma = f_m - \mu N_M& (7)\\ Y) & \to & 0 = -2mg + N_M - N_m & (8) \end{array} \right.$

Resolviendo estas ecuaciones obtenemos

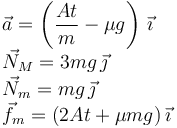
$\begin{array}{l} \vec{a} = \left(\dfrac{At}{m} - \mu g\right)\,\vec{\imath}\\ \vec{N}_{M} = 3mg\,\vec{\jmath}\\ \vec{N}_m = mg\,\vec{\jmath}\\ \vec{f}_m = (2At + \mu mg)\,\vec{\imath} \end{array}$

2.4 Deslizamiento de la masa superior

Igual que antes el deslizamiento ocurre cuando el módulo de la fuerza de rozamiento sobre la masa superior iguala su valor máximo

$|\vec{f}_m| = \mu|\vec{N}_{mN}| \Longrightarrow 2AT+\mu mg = \mu mg \Longrightarrow T=0$

Masa sobre otra masa con rozamiento, Noviembre 2017 (G.I.E.R.M.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Aceleración de las masas

2.2 Deslizamiento de la masa superior

2.3 Rozamiento de la masa inferior con el suelo

2.4 Deslizamiento de la masa superior

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES