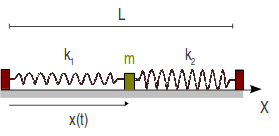
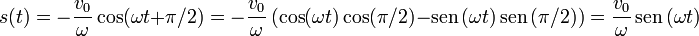Partícula sometida a la acción de dos muelles colineales, Enero 2012 (G.I.C.)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

Se tiene el sistema de la figura, formado por dos muelles de longitud natural nula y constantes elásticas $k 1$ y $k 2$ . Los puntos de anclaje de los muelles están separados por una distancia $L$ . Una partícula de masa $m$ está conectada a los dos muelles y se mueve bajo la acción de éstos. El rozamiento con la superficie es despreciable. 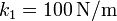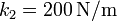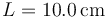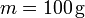Los valores numéricos de los parámetros del problema son $k_1=100\,\mathrm{N/m}$ , $k_2=200\,\mathrm{N/m}$ , $L = 10.0\,\mathrm{cm}$ , $m=100\,\mathrm{g}$ .

Calcula la posición de equilibrio de la partícula.
Calcula la energía potencial elástica de la partícula cuando está en su posición de equilibrio.
Estando la partícula en la posición de equilibrio, se le da un empujón hacia la derecha de modo que su velocidad inicial es $v 0$ . ¿Cuál es el período de las oscilaciones de la partícula?
Si el valor numérico de la velocidad inicial es 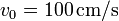$v_0=100\,\mathrm{cm/s}$ , ¿cuál es la amplitud de las oscilaciones de la partícula?

2 Solución

2.1 Posición de equilibrio

Las únicas fuerzas que hay que considerar son las que ejercen los muelles. El peso queda compensado siempre por la fuerza de reacción vincular y no hay rozamiento. Como los muelles tienen longitud natural nula, si la posición de la partícula viene dada por la coordenada $x$ , la fuerza que cada uno de los muelles ejerce sobre ellas es

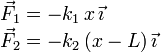
$\begin{array}{l} \vec{F}_1 = -k_1\,x\,\vec{\imath}\\ \vec{F}_2 = -k_2\,(x-L)\,\vec{\imath}\\ \end{array}$

EL muelle 1 tira de la partícula hacia la izquierda y el muelle dos hacia la derecha.

La posición de equilibrio se obtiene imponiendo que la suma de las dos fuerzas es cero

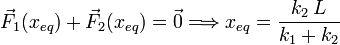
$\vec{F}_1(x_{eq}) + \vec{F}_2(x_{eq}) = \vec{0} \Longrightarrow x_{eq} = \dfrac{k_2\,L}{k_1+k_2}$

Con los datos numéricos del problema tenemos

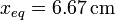
$x_{eq} = 6.67\,\mathrm{cm}$

2.2 Energía elástica en la posición de equilibrio

La energía potencial elástica total es la suma de la energía potencial elástica de cada muelle. Como ambos tienen elongación natural nula, en la posición de equilibrio tenemos

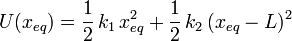
$U(x_{eq}) = \dfrac{1}{2}\,k_1\,x^2_{eq} + \dfrac{1}{2}\,k_2\,(x_{eq} - L)^2$

Sustituyendo los valores numéricos tenemos

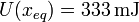
$U(x_{eq}) = 333\,\mathrm{mJ}$

2.3 Período de oscilación

Al separarla de su posición de equilibrio, la partícula se mueve bajo la acción de las fuerzas de los muelles. La Segunda Ley de Newton se escribe

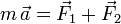
$m\,\vec{a} = \vec{F}_1+\vec{F}_2$

Al ser el movimiento unidireccional, esta ecuación puede escribirse usando sólo las componentes

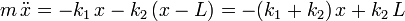
$m\,\ddot{x} = -k_1\,x - k_2\,(x-L) = -(k_1+k_2)\,x + k_2\,L$

Es mejor describir el movimiento respecto de la posición de equilibrio. Definimos

$s (t) = x (t) - x e q$

Y por tanto

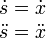
$\begin{array}{l} \dot{s} = \dot{x}\\ \ddot{s} = \ddot{x} \end{array}$

Escribimos la Segunda Ley en términos de la variable $s (t)$

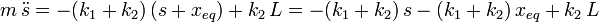
$m\,\ddot{s} = -(k_1+k_2)\,(s+x_{eq}) + k_2\,L = -(k_1+k_2)\,s -(k_1+k_2)\,x_{eq} + k_2\,L$

Teniendo en cuenta la expresión de la posición de equilibrio, los dos últimos sumandos se cancelan. Pasando la masa a la izquierda podemos escribir la ecuación como

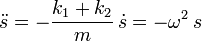
$\ddot{s} = -\dfrac{k_1+k_2}{m}\,\dot{s} = -\omega^2\,s$

Esta es la ecuación de un movimiento armónico simple con frecuencia angular

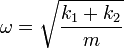
$\omega = \sqrt{\dfrac{k_1+k_2}{m}}$

El período de oscilación es

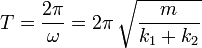
$T = \dfrac{2\pi}{\omega} = 2\pi\,\sqrt{\dfrac{m}{k_1+k_2}}$

Sustituyendo los valores numéricos tenemos

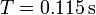
$T = 0.115\,\mathrm{s}$

2.4 Amplitud de las oscilaciones

La situación descrita en el enunciado equivale a las condiciones iniciales

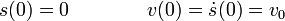
$s(0) = 0\qquad\qquad v(0) = \dot{s}(0) = v_0$

La solución general de la ecuación de movimiento puede escribirse como

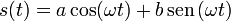
$s(t) = a\cos(\omega t) + b\,\mathrm{sen}\,(\omega t)$

Derivando una vez tenemos

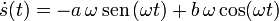
$\dot{s}(t) = -a\,\omega\,\mathrm{sen}\,(\omega t) + b\,\omega\cos(\omega t)$

Imponiendo las condiciones iniciales

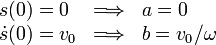
$\begin{array}{lcl} s(0) = 0 & \Longrightarrow & a=0 \\ \dot{s}(0) = v_0 & \Longrightarrow & b = v_0/\omega \end{array}$

El movimiento viene descrito por la función

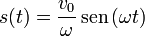
$s(t) = \dfrac{v_0}{\omega}\,\mathrm{sen}\,(\omega t)$

y la amplitud de la oscilación es

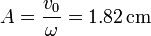
$A = \dfrac{v_0}{\omega} = 1.82\,\mathrm{cm}$

2.4.1 Resolución alternativa

La solución de la ecuación de movimiento también buscarse de la forma

$s (t) = A cos(ω t + φ)$

Derivando una vez tenemos

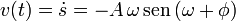
$v(t) = \dot{s} = -A\,\omega\,\mathrm{sen}\,(\omega + \phi)$

Al imponer las condiciones iniciales obtenemos dos ecuaciones

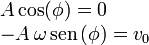
$\begin{array}{l} A\cos(\phi) = 0\\ -A\,\omega\,\mathrm{sen}\,(\phi) = v_0 \end{array}$

Dividimos la segunda ecuación por $ω$ , elevamos las dos al cuadrado y las sumamos. Como $sen 2 α + cos 2 α = 1$ obtenemos

$A = v 0 / ω$

Para obtener $φ$ , observamos que de la primera ecuación obtenemos

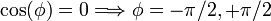
$\cos(\phi) = 0 \Longrightarrow \phi=-\pi/2,+\pi/2$

En la segunda ecuación, si elegimos que $A$ sea positiva, tenemos que el 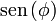$\mathrm{sen}\,(\phi)$ es negativo. Por tanto $φ = - π / 2$ .

La solución final es

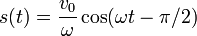
$s(t) = \dfrac{v_0}{\omega}\cos(\omega t - \pi/2)$

Esta solución es equivalente a la anterior. Usando la relación

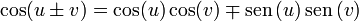
$\cos(u \pm v) = \cos(u)\cos(v) \mp \mathrm{sen}\,(u)\,\mathrm{sen}\,(v)$

vemos que

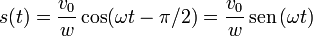
$s(t) = \dfrac{v_0}{w}\cos(\omega t-\pi/2) = \dfrac{v_0}{w}\,\mathrm{sen}\,(\omega t)$

Si hubiéramos supuesto que $A$ es negativa, habríamos obtenido $φ = + π / 2$ , con lo cual la solución sería

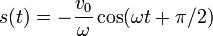
$s(t) = -\dfrac{v_0}{\omega}\cos(\omega t + \pi/2)$

Pero usando la misma relación del coseno de una suma vemos que esta expresión es equivalente a la anterior

$s(t) = -\dfrac{v_0}{\omega}\cos(\omega t + \pi/2) = -\dfrac{v_0}{\omega}\,(\cos(\omega t)\cos(\pi/2) - \mathrm{sen}\,(\omega t)\,\mathrm{sen}\,(\pi/2)) = \dfrac{v_0}{\omega}\,\mathrm{sen}\,(\omega t)$

Partícula sometida a la acción de dos muelles colineales, Enero 2012 (G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Posición de equilibrio

2.2 Energía elástica en la posición de equilibrio

2.3 Período de oscilación

2.4 Amplitud de las oscilaciones

2.4.1 Resolución alternativa

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES