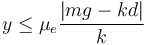De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

En el sistema de la figura el muelle tiene longitud natural nula y constante de recuperación $k$ . La masa de la partícula es $m$ .

Si los vínculos son lisos ¿cuál de las posiciones de la partícula puede ser de equilibrio? ¿Y si los vínculos son rugosos?
Determina las posiciones de equilibrio en los casos en que éste pueda existir.
Supongamos ahora que hay rozamiento. Suponiendo que la posición de la partícula está fijada, calcula la fuerza de rozamiento que debe actuar para que haya equilibrio estático.
A partir del resultado del apartado anterior, encuentra el rango de posiciones de equilibrio en cada uno de los casos.

2 Solución

2.1 Posibles posiciones de equilibrio

2.1.1 Vínculo liso

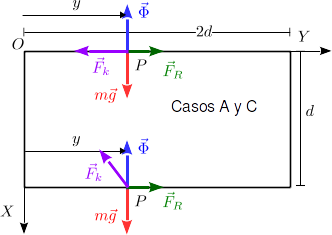
La figura de la derecha muestra las fuerzas que actúan sobre la partícula en cada una de las configuraciones. La fuerza que ejerce el rectángulo sobre ella es siempre perpendicular al hilo correpondiente en cada caso.

En los casos $A$ y $C$ no es posible que haya posiciones de equilibrio. La fuerza vincular puede cancelar el peso, pero no hay ninguna fuerza que pueda cancelar la componente horizontal de la fuerza que ejerce el muelle. En esos dos casos la partícula sufre una fuerza neta necesariamente no nula, por lo que adquiere una aceleración y se pone en movimiento.

En el caso $B$ si es posible encontrar un punto del hilo en que las tres fuerzas se cancelen. El peso puede cancelar la componente vertical de la fuerza elástica y la fuerza vincular puede cancelar la componente horizontal.

En el caso $D$ el peso y la fuerza elástica pueden cancelarse. Como un posible valor de la fuerza vincular es cero, en este caso también puede haber una posición de equilibrio.

En definitiva, puede haber equilibrio en $B$ y $D$ y no puede haberlo en $A$ y $C$ .

Sabemos que la fuerza vincular tiene que apuntar hacia arriba en el caso $A$ , hacia la derecha en el caso $B$ y debe ser nula en el caso $D$ . Pero en el caso $C$ su sentido depende de la posición de la partícula y de los valores de los parámetros del problema.

2.1.2 Vínculo rugoso

El vínculo rugoso implica que, en cada caso, hay que añadir una fuerza de rozamiento paralela al hilo. Ahora puede haber equilibrio en las cuatro configuraciones, pues la fuerza vincular y la de rozamiento pueden siempre ajustarse para cancelar la suma de las otras dos.

Sabemos que la fuerza de rozamiento tiene que apuntar hacia la derecha en los casos $A$ y $C$ . Pero en los casos $B$ y $D$ su sentido depende de la posición de la partícula y de los valores de los parámetros del problema.

2.2 Cálculo de las posiciones de equilibrio cuando existen vínculos lisos

2.2.1 Caso B

La derecha del dibujo muestra el diagrama de cuerpo libre de la partícula en el caso $B$ . Proyectamos las fuerzas en los ejes elegidos en el dibujo

$\begin{array}{l} m\vec{g} = mg\,\vec{\imath}\\ \vec{F}_k = -k\overrightarrow{OP} = -k\,(x\,\vec{\imath} + 2d\,\vec{\jmath})\\ \vec{\Phi} = N_y\,\vec{\jmath} + N_z\,\vec{k} \end{array}$

La fuerza del muelle viene dada por la expresión válida cuando tiene longitud natural nula. La fuerza vincular tiene dos posibles componentes no nulas, pues hay dos movimientos prohibidos para la partícula en las direcciones de los ejes $Y$ y $Z$ . La condición de equilibrio es

$m\vec{g} + \vec{F}_k + \vec{\Phi} = \vec{0}$

Esta ecuación vectorial se descompone en tres ecuaciones escalares, una por cada componente

$\begin{array}{lcl} X) & \to & mg -kx = 0\\ Y) & \to & N_y -2kd = 0\\ Z) & \to & N_z = 0 \end{array}$

Tenemos tres incógnitas ${x, N y, N z}$ y tres ecuaciones, por lo que el problema está bien planteado. Una de las incógnitas está relacionada con la posición de la partícula, $x$ , y las otras dos con las fuerzas vinculares. Esto se debe a que la partícula está sometida a dos vínculos: $y = 2 d$ y $z = 0$ , que eliminan dos grados de libertad, pero añaden dos componentes no nulas de la fuerza vincular.

La posición de equilibrio y la fuerza vincular en esa posición son

$x_{eq}^{l} = \dfrac{mg}{k}\,\qquad \vec{\Phi} = 2kd\,\vec{\jmath}$

2.2.2 Caso D

La izquierda del dibujo muestra el diagrama de cuerpo libre de la partícula en el caso $B$ . Proyectamos las fuerzas en los ejes elegidos en el dibujo

$\begin{array}{l} m\vec{g} = mg\,\vec{\imath}\\ \vec{F}_k = -k\overrightarrow{OP} = -kx\,\vec{\imath}\\ \vec{\Phi} = N_y\,\vec{\jmath} + N_z\,\vec{k} \end{array}$

La condición de equilibrio es

$m\vec{g} + \vec{F}_k + \vec{\Phi} = \vec{0}$

Esta ecuación vectorial se descompone en tres ecuaciones escalares, una por cada componente

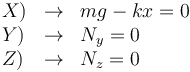
$\begin{array}{lcl} X) & \to & mg -kx = 0\\ Y) & \to & N_y = 0\\ Z) & \to & N_z = 0 \end{array}$

La posición de equilibrio y la fuerza vincular en esa posición son

$x_{eq}^{l} = \dfrac{mg}{k}\,\qquad \vec{\Phi} = \vec{0}$

2.3 Intervalo de posiciones de equilibrio cuando hay rozamiento

2.3.1 Caso B

La diferencia con el caso liso es que hay que añadir una fuerza de rozamiento paralela al hilo. Las otras fuerzas no cambian su expresión. Tenemos

$\begin{array}{l} m\vec{g} = mg\,\vec{\imath}\\ \vec{F}_k = -k\overrightarrow{OP} = -k\,(x\,\vec{\imath} + 2d\,\vec{\jmath})\\ \vec{\Phi} = N_y\,\vec{\jmath} + N_z\,\vec{k}\\ \vec{F}_R = f\,\vec{\imath} \end{array}$

No sabemos a priori el sentido de la fuerza de rozamiento. La solución del problema nos lo dará. La condición de equilibrio es

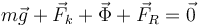
$m\vec{g} + \vec{F}_k + \vec{\Phi} + \vec{F}_R= \vec{0}$

Esta ecuación vectorial se descompone en tres ecuaciones escalares, una por cada componente

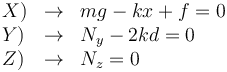
$\begin{array}{lcl} X) & \to & mg -kx + f = 0\\ Y) & \to & N_y -2kd = 0\\ Z) & \to & N_z = 0 \end{array}$

Tenemos cuatro incógnitas ${x, f, N y, N z}$ y tres ecuaciones. Esto quiere decir que el problema tiene múltiples soluciones. Es decir, ahora no hay una posición de equilibrio, sino varias.

El análisis para encontrar el intervalo de posiciones de equilibrio es el siguiente. Primero fijamos la posición de la partícula, es decir, ahora $x$ se considera un dato. Entonces tenemos tres ecuaciones para tres incógnitas: ${f, N y, N z}$ . Obtenemos los valores que deben tener la fuerza de rozamiento y la normal para que haya equilibrio en esa posición

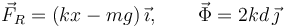
$\vec{F}_R = (kx-mg)\,\vec{\imath}, \qquad \vec{\Phi} = 2kd\,\vec{\jmath}$

Para que esa posición sea de equilibrio, es necesario que la fuerza de rozamiento pueda proporcionar esa fuerza, es decir, que se cumpla

$|\vec{F}_R| \leq \mu_e|\vec{\Phi}|$

Esta condición implica

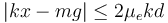
$|kx-mg| \leq 2\mu_e kd$

Hemos de considerar dos casos

$kx>mg \Longrightarrow |kx-mg| = kx-mg \leq 2kd \Longrightarrow x\leq x_{max} = \dfrac{mg}{k} + 2\mu_ed$

En el caso contrario

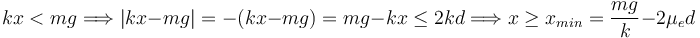
$kx<mg \Longrightarrow |kx-mg| = -(kx-mg) = mg-kx \leq 2kd \Longrightarrow x\geq x_{min} = \dfrac{mg}{k} - 2\mu_ed$

Entonces, para que el equilibrio sea posible debe cumplirse

$x\in [x_{min}, x_{max}]$

con

$x_{min} = \dfrac{mg}{k} - 2\mu_ed, \qquad x_{max} = \dfrac{mg}{k} + 2\mu_ed$

Si se cumple esa condición, las fuerzas de rozamiento y normal valen

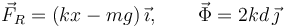
$\vec{F}_R = (kx-mg)\,\vec{\imath}, \qquad \vec{\Phi} = 2kd\,\vec{\jmath}$

El efecto del rozamiento ha sido pasar de la existencia de un punto de equilibrio a la existencia de un intervalo de posiciones de equilibrio. Este intervalo corresponde a puntos por encima y por debajo del punto de equilibrio del caso liso.

2.3.2 Caso D

Procedemos igual que en el caso $D$

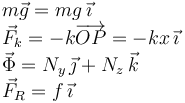
$\begin{array}{l} m\vec{g} = mg\,\vec{\imath}\\ \vec{F}_k = -k\overrightarrow{OP} = -kx\,\vec{\imath}\\ \vec{\Phi} = N_y\,\vec{\jmath} + N_z\,\vec{k}\\ \vec{F}_R = f\,\vec{\imath} \end{array}$

No sabemos a priori el sentido de la fuerza de rozamiento. La solución del problema nos lo dará. La condición de equilibrio es

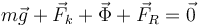
$m\vec{g} + \vec{F}_k + \vec{\Phi} + \vec{F}_R= \vec{0}$

Esta ecuación vectorial se descompone en tres ecuaciones escalares, una por cada componente

$\begin{array}{lcl} X) & \to & mg -kx + f = 0\\ Y) & \to & N_y = 0\\ Z) & \to & N_z = 0 \end{array}$

Este es un caso especial. La fuerza normal es nula. Esto quiere decir que no hay fuerza de rozamiento. Esto se debe a que, en realidad, no hay contacto entre la partícula y el hilo. En un experimento real esto no sería así. Por ejemplo, el muelle no estaría completamente alineado con el hilo, por lo que ejercería una pequeña fuerza horizontal que produciría rozamiento.

En este caso, en la situación ideal contemplada aquí, sólo existiría la posición de equilibrio del caso liso.

2.3.3 Caso A

En este caso no hay posición de equilibrio cuando el vínculo es liso. La fuerza de rozamiento va a hacer que aparezca un intervalo de posiciones de equilibrio.

Del dibujo vemos que las fuerzas sobre la partícula son

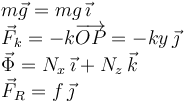
$\begin{array}{l} m\vec{g} = mg\,\vec{\imath}\\ \vec{F}_k = -k\overrightarrow{OP} = -ky\,\vec{\jmath}\\ \vec{\Phi} = N_x\,\vec{\imath} + N_z\,\vec{k}\\ \vec{F}_R = f\,\vec{\jmath} \end{array}$

Aquí sabemos que la fuerza de rozamiento debe apuntar hacia la derecha, es decir, $f$ debe ser positiva, debido a la elección de los ejes. La condición de equilibrio es

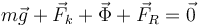
$m\vec{g} + \vec{F}_k + \vec{\Phi} + \vec{F}_R= \vec{0}$

Esta ecuación vectorial se descompone en tres ecuaciones escalares, una por cada componente

$\begin{array}{lcl} X) & \to & mg + N_x = 0\\ Y) & \to & -ky + f = 0\\ Z) & \to & N_z = 0 \end{array}$

De nuevo tenemos cuatro incógnitas ${y, f, N x, N z}$ y tres ecuaciones. Esto indica que hay varias posiciones de equilibrio. Fijamos el valor de $y$ y calculamos las fuerzas de rozamiento y normal para que haya equilibrio para esa posición fijada

$\vec{F}_R = ky\,\vec{\jmath}\, \qquad \vec{\Phi} = -mg\,\vec{\imath}$

Para que esta posición sea posible el módulo de la fuerza de rozamiento no debe sobrepasar su valor máximo

$|\vec{F}_R| \leq \mu_e|\vec{\Phi}| \Longrightarrow ky \leq \mu_e mg$

Entonces, el rango de posiciones de equilibrio es

$y\leq \mu_e\dfrac{mg}{k}$

2.3.4 Caso C

Este caso es similar al $A$ La fuerza de rozamiento va a hacer que aparezca un intervalo de posiciones de equilibrio.

Del dibujo vemos que las fuerzas sobre la partícula son

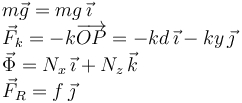
$\begin{array}{l} m\vec{g} = mg\,\vec{\imath}\\ \vec{F}_k = -k\overrightarrow{OP} = -kd\,\vec{\imath} -ky\,\vec{\jmath}\\ \vec{\Phi} = N_x\,\vec{\imath} + N_z\,\vec{k}\\ \vec{F}_R = f\,\vec{\jmath} \end{array}$

Aquí sabemos que la fuerza de rozamiento debe apuntar hacia la derecha, es decir, $f$ debe ser positiva, debido a la elección de los ejes. Sin embargo no conocemos a priori el sentido de la fuerza vincular normal. La condición de equilibrio es

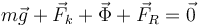
$m\vec{g} + \vec{F}_k + \vec{\Phi} + \vec{F}_R= \vec{0}$

Esta ecuación vectorial se descompone en tres ecuaciones escalares, una por cada componente

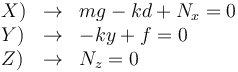
$\begin{array}{lcl} X) & \to & mg -kd + N_x = 0\\ Y) & \to & -ky + f = 0\\ Z) & \to & N_z = 0 \end{array}$

De nuevo tenemos cuatro incógnitas ${y, f, N x, N z}$ y tres ecuaciones. Esto indica que hay varias posiciones de equilibrio. Fijamos el valor de $y$ y calculamos las fuerzas de rozamiento y normal para que haya equilibrio para esa posición fijada

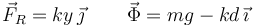
$\vec{F}_R = ky\,\vec{\jmath}\, \qquad \vec{\Phi} = mg - kd\,\vec{\imath}$

Para que esta posición sea posible el módulo de la fuerza de rozamiento no debe sobrepasar su valor máximo

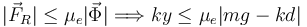
$|\vec{F}_R| \leq \mu_e|\vec{\Phi}| \Longrightarrow ky \leq \mu_e |mg-kd|$

Entonces la condición de equilibrio en este caso es

$y\leq \mu_e \dfrac{|mg-kd|}{k}$

Partiícula en un rectángulo con muelle

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Posibles posiciones de equilibrio

2.1.1 Vínculo liso

2.1.2 Vínculo rugoso

2.2 Cálculo de las posiciones de equilibrio cuando existen vínculos lisos

2.2.1 Caso B

2.2.2 Caso D

2.3 Intervalo de posiciones de equilibrio cuando hay rozamiento

2.3.1 Caso B

2.3.2 Caso D

2.3.3 Caso A

2.3.4 Caso C

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES