De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

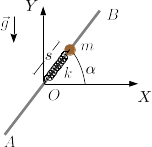
Una partícula de masa $m$ puede moverse a lo largo de una barra de longitud $L$ . La partícula está conectada al extremo de un muelle de constante elástica $k$ y longitud natural nula. El ángulo que forma la barra con el eje horizontal $O X$ es $α$ , y no cambia con el tiempo. La gravedad actúa como se indica en la figura. El coeficiente de rozamiento estático entre la partícula y la barra es $μ$ .

Dibuja el diagrama de cuerpo libre de la partícula, así como la expresión de las fuerzas que actúan sobre ella.
Suponiendo que no hay rozamiento, determina el valor de equilibrio de $s$ ( $s = 0$ corresponde al punto $O$ de la barra).
Si ahora incluimos el rozamiento, calcula el rango posible de valores de equilibrio de $s$ .
Supongamos de nuevo que no hay rozamiento. Encuentra la expresión del vector velocidad y aceleración de la partícula.
Aplicando la Segunda Ley de Newton, encuentra la ecuación de movimiento, así como la frecuencia de las oscilaciones.

2 Solución

2.1 Fuerzas sobre la partícula

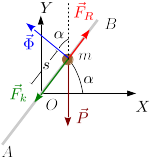
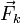La figura de la derecha muestra las fuerzas que actúan sobre la partícula: el peso $\vec{P}$ , la fuerza del muelle $\vec{F}_k$ , la fuerza vincular $\vec{\Phi}$ , normal a la barra, y la fuerza de rozamiento $\vec{F}_R$ , paralela a la barra. La expresión de las fuerzas en el sistema de ejes de la figura es

$\begin{array}{l} \vec{P} = -mg\,\vec{\jmath} \\ \vec{F}_k = -ks\,(\cos\alpha\,\vec{\imath} + \mathrm{sen}\,\alpha\,\vec{\jmath}) \\ \vec{\Phi} = N\,(-\mathrm{sen}\,\alpha\,\vec{\imath} + \cos\alpha\,\vec{\jmath}) \\ \vec{F}_R = f\,(\cos\alpha\,\vec{\imath} + \mathrm{sen}\,\alpha\,\vec{\jmath}) \end{array}$

El valor de $α$ es un dato del problema.

2.2 Equilibrio sin rozamiento

La condición de equilibrio en este caso es

$\vec{P} + \vec{F}_k + \vec{\Phi}=\vec{0} \Longrightarrow \left\{ \begin{array}{lclr} (X) & \to & -ks\cos\alpha - N\,\mathrm{sen}\,\alpha = 0 & (1) \\ (Y) & \to & -mg -ks\,\mathrm{sen}\,\alpha +N\cos\alpha=0 & (2) \end{array} \right.$

Las incógnitas son ${s, N}$ y tenemos dos ecuaciones. Multiplicando la primera ecuación por $cosα$ , la segunda por 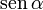$\mathrm{sen}\,\alpha$ y sumándolas obtenemos

$(1)\times\cos\alpha + (2)\times\,\mathrm{sen}\,\alpha \Longrightarrow -ks -mg\,\mathrm{sen}\,\alpha = 0 \Longrightarrow s_{eq}^0 = -\dfrac{mg\,\mathrm{sen}\,\alpha}{k}$

La posición de equilibrio está a la izquierda y debajo del punto $O$ . Si $α = 0$ la posición de equilibrio es $s = 0$ , lo cual tiene sentido.

Para la fuerza vincular tenemos

$N = mg\cos\alpha \Longrightarrow \vec{\Phi} = mg\cos\alpha\,(-\mathrm{sen}\alpha\,\vec{\imath} + \cos\alpha\,\vec{\jmath})$

Si $α = 0$ (barra horizontal) es igual al peso con sentido contrario. Si $α = π / 2$ ( barra vertical) se anula. Esto también tiene sentido.

2.3 Equilibrio con rozamiento

La condición de equilibrio ahora es

$\vec{P} + \vec{F}_k + \vec{\Phi} + \vec{F}_R=\vec{0} \Longrightarrow \left\{ \begin{array}{lclr} (X) & \to & -ks\cos\alpha - N\,\mathrm{sen}\,\alpha + f\cos\alpha = 0 & (3) \\ (Y) & \to & -mg -ks\,\mathrm{sen}\,\alpha +N\cos\alpha + f\,\mathrm{sen}\,\alpha =0 & (4) \end{array} \right.$

Ahora tenemos tres incógnitas: ${s, N, f}$ y sólo dos ecuaciones. Lo que hacemos es fijar la posición de la partícula $s = s 0$ , con lo que las incógnitas son ${N, f}$ . Haciendo una operación similar a la anterior tenemos

$(3)\times\cos\alpha + (4)\times\,\mathrm{sen}\,\alpha \Longrightarrow -ks_0 -mg\,\mathrm{sen}\,\alpha + f = 0 \Longrightarrow f = ks + mg\,\mathrm{sen}\,\alpha$

Recordemos que $s$ puede ser negativa. Para la fuerza normal obtenemos

$N = m g cosα$

Para que haya equilibrio debe cumplirse

$|\vec{F}_R|\leq \mu |\vec{\Phi}| \Longrightarrow |f|\leq \mu N$

Como $s$ puede ser negativa, tenemos que contemplar dos posibles situaciones. La primera es

$mg\,\mathrm{sen}\,\alpha + ks >0 \Longrightarrow |f| = mg\,\mathrm{sen}\,\alpha + ks \Longrightarrow mg\,\mathrm{sen}\,\alpha + ks \leq \mu mg\cos\alpha$

Para que este ocurre tiene que cumplirse

$s\leq \dfrac{mg}{k}(\mu\cos\alpha - \mathrm{sen}\,\alpha) = s_{max}$

La otra posibilidad es

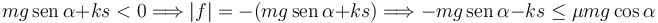
$mg\,\mathrm{sen}\,\alpha + ks <0 \Longrightarrow |f| = -(mg\,\mathrm{sen}\,\alpha + ks) \Longrightarrow -mg\,\mathrm{sen}\,\alpha - ks \leq \mu mg\cos\alpha$

Para que este ocurre tiene que cumplirse

$s\geq -\dfrac{mg}{k}(\mu\cos\alpha + \mathrm{sen}\,\alpha) = s_{min}$

Es decir, para que se pueda cumplir la condición de equilibrio sin rozamiento debe ocurrir que el valor de $s$ cumpla

$s\in[s_{min}, s_{max}] = \left[ s_{eq}^0 + \mu\dfrac{mg}{k}\cos\alpha, s_{eq}^0 - \mu\dfrac{mg}{k}\cos\alpha \right]$

Al incluir el rozamiento hay varias posiciones de equilibrio. Los límites inferior y superior del intervalo están a la izquierda y a la derecha de la posición de equilibrio sin rozamiento, $s_{eq}^0$ .

2.4 Vectores velocidad y aceleración

El ángulo $α$ es fijo. Cuando la partícula se mueve tenemos $s = s (t)$ . Entonces

$\begin{array}{l} \vec{r} = s\,(\cos\alpha\,\vec{\imath} + \mathrm{sen}\,\alpha\,\vec{\jmath}) \\ \vec{v} = \dot{\vec{r}} = \dot{s}\,(\cos\alpha\,\vec{\imath} + \mathrm{sen}\,\alpha\,\vec{\jmath}) \\ \vec{a} = \dot{\vec{v}} = \ddot{s}\,(\cos\alpha\,\vec{\imath} + \mathrm{sen}\,\alpha\,\vec{\jmath}) \end{array}$

2.5 Ecuación de movimiento sin rozamiento

La ecuación de movimiento es la Segunda Ley de Newton. Tenemos

$m\vec{a} = \vec{P} + \vec{F}_k + \vec{\Phi} \Longrightarrow \left\{ \begin{array}{lclr} (X) & \to & m\ddot{s}\cos\alpha = -ks\cos\alpha - N\,\mathrm{sen}\,\alpha & (5) \\ (Y) & \to & m\ddot{s}\,\mathrm{sen}\,\alpha = -mg -ks\,\mathrm{sen}\,\alpha +N\cos\alpha & (6) \end{array} \right.$

Obtenemos la ecuación de movimiento

$(5)\times\cos\alpha + (6)\times\,\mathrm{sen}\,\alpha \Longrightarrow m\ddot{s} = -ks -mg\,\mathrm{sen}\,\alpha \Longrightarrow \ddot{s} = -\dfrac{k}{m}s -g\,\mathrm{sen}\,\alpha$

Esta es la ecuación de movimiento de un oscilador armónico con frecuencia angular y período

$\omega = \sqrt{\dfrac{k}{m}}, \qquad T = \dfrac{2\pi}{\omega} = 2\pi\sqrt{\dfrac{m}{k}}$

Masa en barra fija con muelle, Sept 2017 (G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Fuerzas sobre la partícula

2.2 Equilibrio sin rozamiento

2.3 Equilibrio con rozamiento

2.4 Vectores velocidad y aceleración

2.5 Ecuación de movimiento sin rozamiento

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES