Partícula en semiaro con muelle anclado en un extremo, Noviembre 2016 (G.I.C.)
De Laplace
Contenido |
1 Enunciado
Una partícula de masa m está engarzada en un semiaro de radio R cuyo centro coincide con el origen de coordenadas, como se observa en la figura. La partícula está conectada a un muelle de constante elástica k y longitud natural nula conectada al punto A. La gravedad actúa hacia abajo.
- Dibuja el diagrama de cuerpo libre de la partícula en situación de contacto rugoso, indicando de que fuerzas se conoce su dirección y sentido y de cuales no.
- Escribe la expresión que da la fuerza que el muelle ejerce sobre la partícula.
- En situación de contacto liso, encuentra el valor del ángulo de equilibrio.
- Supongamos ahora que el contacto es rugoso con un coeficiente de rozamiento estático μ. Además el ángulo θ es tal que cosθ = 3 / 5, y el sistema se ajusta de modo que mg = kR. ¿Cuál es valor mínimo del coeficiente de rozamiento para que esta configuración sea de equilibrio?
2 Solución
2.1 Diagrama de cuerpo libre
La figura de la derecha muestra las fuerzas que actúan sobre la partícula y sus direcciones. La del muelle apunta hacia el punto A y el peso hacia abajo. La fuerza  tiene dirección radial, pues debe ser perpendicular al aro. Además, sabemos que debe apuntar hacia fuera, pues el muelle, al tener longitud natural nula, siempre intenta contraerse. La fuerza de rozamiento es tangente al semiaro, pero no conocemos su sentido a priori. Depende de la posición de la partícula y de los valores de los parámetros del muelle y la partícula.
tiene dirección radial, pues debe ser perpendicular al aro. Además, sabemos que debe apuntar hacia fuera, pues el muelle, al tener longitud natural nula, siempre intenta contraerse. La fuerza de rozamiento es tangente al semiaro, pero no conocemos su sentido a priori. Depende de la posición de la partícula y de los valores de los parámetros del muelle y la partícula.
2.2 Expresión de la fuerza del muelle
Al tener longitud natural nula, la fuerza que ejerce el muelle sobre la partícula es
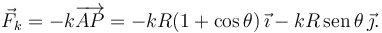
Hemos usado que las coordenadas de los puntos A y P son, respectivamente
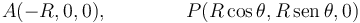
2.3 Angulo de equilibrio con contacto liso
Cuando el contacto es liso no hay que incluir la fuerza de rozamiento. Además de la fuerza ejercida por el muelle (activa) tenemos la fuerza del peso (activa) y la que ejerce el aro (reacción vincular). Del peso conocemos su valor completo y de la reacción sólo su dirección y sentido, pero no su magnitud. Tenemos
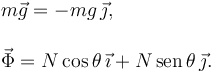
La condición de equilibrio es que el sumatorio de fuerzas es cero. Esto nos da dos ecuaciones escalares, una por componente
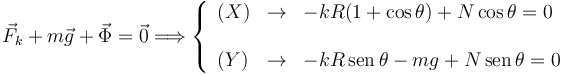
Multiplicando la primera ecuación por 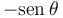 , la segunda por cosθ y sumándolas obtenemos
, la segunda por cosθ y sumándolas obtenemos
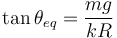
Si el muelle es muy débil, entonces 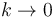 y la tangente se hace infinito, es decir,
y la tangente se hace infinito, es decir,  , el punto mas alto del semiaro. Esa sería la posición de equilibrio si no hubiera muelle. Por otro lado, si no hubiese gravedad, la tangente sería cero y
, el punto mas alto del semiaro. Esa sería la posición de equilibrio si no hubiera muelle. Por otro lado, si no hubiese gravedad, la tangente sería cero y 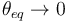 , es decir, la posición de equilibrio sería el punto opuesto a A, como es lógico.
, es decir, la posición de equilibrio sería el punto opuesto a A, como es lógico.
La otra ecuación nos da la magnitud de la fuerza de reacción vincular. Esta fuerza es
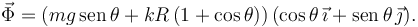
Analizando de nuevo los dos límites anteriores tenemos

2.4 Análisis con contacto rugoso
La presencia del rozamiento hace que, en vez de tener un punto de equilibrio, tengamos un intervalo de puntos de equilibrio sobre el semiaro. Hay que cambiar la manera de afrontar el problema. Primero nos preguntamos, para un valor dado del ángulo, cuál debe ser el valor de las fuerzas vincular y de rozamiento para que haya equilibrio. La fuerza de rozamiento es

La condición de equilibrio nos da de nuevo dos ecuaciones escalares

El problema nos dice que consideremos la situación en que cosθ = 3 / 5. Tenemos entonces
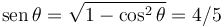
Además consideramos mg = kR. Entonces las dos ecuaciones quedan

Multiplicando la primera por 3 y la segunda por 4, y sumándolas tenemos
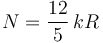
Por tanto
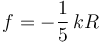
El signo menos indica que la fuerza de rozamiento apunta hacia la derecha. Ahora bien, para que esta situación sea de equilibrio debe ocurrir
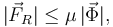
lo que nos da la condición