Problemas del segundo principio de la termodinámica
De Laplace
(→Solución) |
|||
| (55 ediciones intermedias no se muestran.) | |||
| Línea 3: | Línea 3: | ||
[[Ejemplo de máquina térmica|'''Solución''']] | [[Ejemplo de máquina térmica|'''Solución''']] | ||
| - | |||
==[[Rendimiento de un ciclo recorrido por un gas ideal]]== | ==[[Rendimiento de un ciclo recorrido por un gas ideal]]== | ||
| Línea 33: | Línea 32: | ||
[[Ejemplo de frigorífico de Carnot|'''Solución''']] | [[Ejemplo de frigorífico de Carnot|'''Solución''']] | ||
| + | ==[[Rendimiento de un aparato de aire acondicionado]]== | ||
| + | Para refrescar una habitación se emplea un aparato de aire acondicionado con un coeficiente de despeño (COP o <math>\eta</math>) de 4. El exterior se encuentra a 34°C mientras que el interior del despacho se mantiene a 24°C. El despacho, que esta vacío, tiene una ventana de vidrio por la cual entra calor desde el exterior. | ||
| - | + | # Si el calor que entra por la ventana en la unidad de tiempo es <math>Q=4224\,\mathrm{W}</math>, calcule el trabajo por segundo (potencia) que debe realizar el aparato para mantener la temperatura interior y la cantidad de calor que es arrojada al exterior. | |
| - | + | # Determine el COP máximo que podría tener un aparato de aire acondicionado que operara entre estas dos temperaturas. | |
| + | # Halle la potencia mínima que se requeriría para extraer la misma cantidad de calor por segundo, así como la potencia extra que requiere el aparato real. | ||
| + | # Demuestre que el calor que entra por segundo en la habitación coincide con el valor dado en el primer apartado, si las dimensiones de la ventana son de 5 mm de espesor, 160 cm de ancho y 120 cm de alto. La conductividad calorífica del vidrio es <math>k = 1.1\,\mathrm{W}/(\mathrm{m}\cdot\mathrm{K})</math>. | ||
| + | # Si se sustituye el cristal por uno doble, formado por dos láminas de vidrio como la anterior, entre las cuales hay una capa de aire de 2 cm de espesor, con una conductividad térmica efectiva <math>k'= 0.025\,\mathrm{W}/(\mathrm{m}\cdot\mathrm{K})</math>, ¿cómo cambian los resultados anteriores? | ||
| - | [[ | + | [[Rendimiento de un aparato de aire acondicionado|'''Solución''']] |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
==[[ Variación de entropía en el paso de hielo a vapor ]]== | ==[[ Variación de entropía en el paso de hielo a vapor ]]== | ||
| Línea 64: | Línea 58: | ||
[[Inmersión de un bloque metálico en agua|'''Solución''']] | [[Inmersión de un bloque metálico en agua|'''Solución''']] | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
==[[Comparación de dos variaciones de entropía]]== | ==[[Comparación de dos variaciones de entropía]]== | ||
| Línea 80: | Línea 69: | ||
[[Comparación de dos variaciones de entropía|'''Solución''']] | [[Comparación de dos variaciones de entropía|'''Solución''']] | ||
| - | ==[[ | + | ==[[Variación de entropía con un baño térmico]]== |
| - | Un | + | Un tanque de volumen constante contiene 100 moles de aire a una presión de 100 kPa y una temperatura de 327°C. El aire se enfría hasta la temperatura del ambiente de 27.0°C. Suponiendo que el aire se comporta como un gas ideal diatómico, determine la variación de entropía del aire y del Universo durante el proceso. |
| - | + | ||
| - | + | ||
| - | + | [[Variación de entropía con un baño térmico|'''Solución''']] | |
| - | + | ||
| - | + | ||
| - | [[ | + | ==[[Fusión de hielo en un recipiente]]== |
| + | Se tiene un bloque de hielo de masa <math>m_h = 500\,\mathrm{g}</math> de hielo sumergido en un volumen de agua de masa <math>m_a = 500\,\mathrm{g}</math>, ambos a una temperatura <math>T_a = 0.00 ^\circ\mathrm{C}</math> . El conjunto está contenido en un recipiente | ||
| + | cilíndrico de vidrio, de diámetro <math>d = 16.0\,\mathrm{cm}</math> y espesor <math>e = 1.00\,\mathrm{cm}</math>, abierto por arriba al aire (que se puede suponer un aislante térmico perfecto). El recipiente está sumergido en un baño de agua a <math>T_b = 20.0 ^\circ \mathrm{C}</math>. | ||
| - | + | # Calcula la superficie de agua en contacto con el recipiente y la cantidad de calor que entra en él en 1.00 s. | |
| - | + | # Halla la cantidad de hielo que se funde en el mismo tiempo. ¿Cuánto tiempo tardará en derretirse por completo? | |
| + | # Calcula la variación de entropía en el sistema, en el ambiente y la variación de entropía total en la fusión completa del hielo. | ||
| + | # Supón que en lugar de permitir que el calor fluya directamente desde el baño al sistema se hace pasar por una máquina térmica reversible que opera entre las dos temperaturas. ¿Qué trabajo puede producirse hasta que el hielo se funde completamente? ¿Cuánto calor sale del baño en ese caso? Calcula la variación de entropía del Universo en este proceso. | ||
| - | + | '''Datos:''' Densidad de masa del agua líquida <math>\rho = 1.00\,\mathrm{g}/\mathrm{cm}^3</math>; Conductividad térmica del vidrio <math>k= 1.1\,\mathrm{W}/\mathrm{m}\cdot\mathrm{K}</math>; Entalpía específica de fusión: <math>L_f = \Delta h_f = 333.55\,\mathrm{kJ}/\mathrm{kg}</math> | |
| - | + | [[Fusión de hielo en un recipiente|'''Solución''']] | |
| - | + | ||
| - | + | ==[[Refrigerador alimentado por una máquina térmica]]== | |
| - | + | Un refrigerador que funciona entre una temperatura de -23 °C y la temperatura ambiente de 27 °C posee un coeficiente de desempeño de 3. Para hacer funcionar este refrigerador se emplea una máquina térmica que funciona entre 227 °C y la misma temperatura ambiente, la cual tiene un rendimiento de 0.2. Todo el trabajo producido por la máquina térmica se emplea en hacer funcionar el | |
| - | + | refrigerador. | |
| - | + | ||
| - | + | ||
| - | + | # Definimos la eficiencia del conjunto máquina más refrigerador como el calor extraído del foco frío dividido por el calor que es necesario extraer del foco caliente, ¿cuál es la eficiencia del conjunto? | |
| + | # Si se necesitan extraer 100 J por segundo del foco frío, ¿cuánto calor hay que extraer del foco caliente para hacer funcionar el sistema? ¿Cuánto trabajo realiza en la unidad de tiempo la máquina sobre el refrigerador? | ||
| + | # Calcule la producción de entropía en la unidad de tiempo debida a este conjunto. | ||
| + | # Si tanto el refrigerador como la máquina térmica fueran máquinas de Carnot, ¿cuál sería la eficiencia máxima del conjunto? ¿Qué calor sería necesario sacar del foco caliente en ese caso para extraer 100 J/s del foco frío? | ||
| - | + | [[Refrigerador alimentado por una máquina térmica|'''Solucion''']] | |
| - | + | ||
| - | |||
==[[Eficiencia de un ciclo Otto]]== | ==[[Eficiencia de un ciclo Otto]]== | ||
| Línea 118: | Línea 105: | ||
<center><math>\eta = 1-\frac{1}{r^{\gamma-1}}</math></center> | <center><math>\eta = 1-\frac{1}{r^{\gamma-1}}</math></center> | ||
| - | siendo <math>r = V_A/V_B</math> la ''razón de compresión''. Para ello, halle el rendimiento a partir del calor que entra en el sistema y el que sale de él; exprese el resultado en términos de las temperaturas en los vértices del ciclo y, con ayuda de la ley de Poisson, relacione este resultado con los volúmenes <math>V_A</math> y <math>V_B</math>. | + | siendo <math>r = V_A/V_B</math> la ''razón de compresión'' igual al cociente entre el volumen al inicio del ciclo de compresión y al final de él. Para ello, halle el rendimiento a partir del calor que entra en el sistema y el que sale de él; exprese el resultado en términos de las temperaturas en los vértices del ciclo y, con ayuda de la ley de Poisson, relacione este resultado con los volúmenes <math>V_A</math> y <math>V_B</math>. |
[[Eficiencia de un ciclo Otto|'''Solución''']] | [[Eficiencia de un ciclo Otto|'''Solución''']] | ||
| Línea 126: | Línea 113: | ||
[[Caso práctico de ciclo Otto|'''Solución''']] | [[Caso práctico de ciclo Otto|'''Solución''']] | ||
| + | |||
| + | ==[[Eficiencia de un ciclo Diesel]]== | ||
| + | [[Imagen:ciclo-diesel.png|300px|right]]Un motor diésel puede modelarse con el ciclo ideal formado por seis pasos reversibles, según se indica en la figura. Pruebe que el rendimiento de este ciclo viene dado por la expresión | ||
| + | |||
| + | <center><math>\eta = 1 -\frac{1}{\gamma r^{\gamma-1}}\,\frac{r_c^\gamma-1}{r_c-1}</math></center> | ||
| + | |||
| + | siendo <math>r = V_A/V_B</math> la razón de compresión y <math>r_c = V_C/V_B</math> la relación de combustión. El método para obtener este resultado es análogo al empleado para el [[ciclo Otto]]. Compare los rendimientos del ciclo de Otto y el diésel. ¿Cuáles son las ventajas e | ||
| + | inconvenientes respectivos? | ||
| + | |||
| + | ==[[Caso práctico de ciclo Diesel]]== | ||
| + | Suponga un motor diésel con una capacidad máxima de 1900 cm³. aEn este motor el aire a la entrada está a una presión de 1 atm y una temperatura de 17°C. Si para este motor la razón de compresión es 18 y la de combustión vale 2, determine los volúmenes, presiones y temperaturas de cada vértice del ciclo, así como su rendimiento y el calor y el trabajo intercambiados por el motor. | ||
==[[Eficiencia de un ciclo Brayton]]== | ==[[Eficiencia de un ciclo Brayton]]== | ||
| Línea 132: | Línea 130: | ||
<center><math>\eta = 1-\frac{1}{r^{(\gamma-1)/\gamma}}</math></center> | <center><math>\eta = 1-\frac{1}{r^{(\gamma-1)/\gamma}}</math></center> | ||
| - | siendo <math>r = | + | siendo <math>r = p_B/p_A</math> la ''relación de presión'' igual al cociente entre la presión al final del proceso de compresión y al inicio de él. El método para obtener este resultado es análogo al empleado para el [[Eficiencia de un ciclo Otto|ciclo Otto]]. |
[[Eficiencia de un ciclo Brayton|'''Solución''']] | [[Eficiencia de un ciclo Brayton|'''Solución''']] | ||
| Línea 140: | Línea 138: | ||
[[Caso práctico de ciclo Brayton|'''Solución''']] | [[Caso práctico de ciclo Brayton|'''Solución''']] | ||
| + | |||
| + | ==[[Caso práctico de ciclo de Stirling]]== | ||
| + | 100 moles de gas ideal diátomico sufre un ciclo de Stirling internamente reversible, representado en la figura. El ciclo se compone de dos isotermas y dos isócoras. Las temperaturas de trabajo son <math>T_f = 300\,\mathrm{K}</math> y <math>T_f = 2000\,\mathrm{K}</math>, mientras que las presiones extremas son <math>P_a = 150\,\mathrm{kPa}</math> y <math>P_b = 3.00\,\mathrm{MPa}</math>. | ||
| + | |||
| + | # En cada uno de los procesos, calcula la variación de energía interna, el trabajo realizado y el calor absorbido por el gas. Calcula el rendimiento del ciclo. | ||
| + | # Calcula la variación de entropía en cada proceso del ciclo y la variación neta en el ciclo completo. | ||
| + | # Compara el rendimiento del ciclo con el de una máquina de Carnot reversible que trabaje entre las mismas temperaturas. | ||
| + | # Imagina y describe un experimento que te permita recorrer el ciclo. | ||
| + | |||
| + | '''Dato:''' <math>R = 8.31\,\mathrm{J}/\mathrm{mol}\cdot\mathrm{K}</math> | ||
| + | |||
| + | [[Caso práctico de ciclo de Stirling|'''Solución''']] | ||
| + | |||
| + | ==[[Máximo aprovechamiento del calor]]== | ||
| + | Suponga que se tiene un bloque de 10 kg de hierro (<math>c_p=0.46\,\mathrm{kJ}/\mathrm{kg}\cdot\mathrm{K}</math>) a una temperatura de 200°C y se quiere usar para caldear una gran habitación a una temperatura <math>T_0 = 22^\circ\mathrm{C}</math>, estando el exterior a 5°C. | ||
| + | |||
| + | # Si se coloca el bloque directamente en la habitación, calcule el calor que libera al ambiente. | ||
| + | # Halle la variación de entropía del bloque y del universo en el caso anterior. | ||
| + | # El calor del bloque puede aprovecharse para producir algún trabajo. Para ello, suponga que cuando el bloque se encuentra a una temperatura <math>T</math>, y libera una cantidad de calor <math>mc_p\,\mathrm{d}T</math>, dicho calor se hace pasar por una máquina reversible que opera entre la temperatura <math>T</math> y la del ambiente. Calcule el trabajo obtenible en este paso y la cantitad total de trabajo que se podría obtener. | ||
| + | # Compruebe que el trabajo perdido es igual a <math>T_0\Delta S_\mathrm{u}</math> | ||
| + | # Si ese trabajo se aprovechara para hacer funcionar una bomba de calor reversible que operara entre el exterior y la habitación, ¿cuánto sería el calor total que se liberaría en la habitación? | ||
| + | |||
| + | [[Máximo aprovechamiento del calor|'''Solución''']] | ||
| + | |||
| + | ==[[Contacto reversible entre dos recipientes]]== | ||
| + | Se tienen dos recipientes adiabáticos que contienen 400 y 600 g de agua líquida, respectivamente. La temperatura del primer recipiente es de 0.00 °C y la del segundo 100 °C. | ||
| + | |||
| + | # Los dos recipientes se ponen en contacto térmico a través e una pared diaterma. calcula: | ||
| + | ## La temperatura final del agua. | ||
| + | ## Las cantidades de calor transferidas en el proceso. | ||
| + | ## La variación de entropía en el Universo. | ||
| + | # Supón ahora que el contacto térmico no se hace poniendo los sistemas en contacto, sino a través de una máquina térmica reversible que usa los recipientes como foco caliente y frío, de modo que sus temperaturas van cambiando en el tiempo. Si todos los procesos son reversibles… | ||
| + | ## Calcula la temperatura final del agua en este caso. | ||
| + | ## Calcula el calor cedido por el agua caliente y el absorbido por el agua fría. | ||
| + | ## Determina la cantidad de trabajo que se puede extraer del sistema con este procedimiento. | ||
| + | |||
| + | [[Contacto reversible entre dos recipientes|'''Solución''']] | ||
| + | |||
| + | == Otros problemas == | ||
| + | ===[[Ejemplo de bomba de calor de Carnot]]=== | ||
| + | Una bomba de calor se emplea para mantener caliente una vivienda que se encuentra a 20.0°C siendo la temperatura exterior -5.00°C. Suponiendo que la bomba de calor es una máquina de Carnot invertida, calcule cuantos julios de energía procedentes del medio ambiente exterior serán transferidos al interior de la vivienda por cada julio de energía eléctrica consumida. Explique las ventajas e incovenientes de este sistema de calefacción frente a uno convencional de disipación de energía en una resistencia eléctrica. | ||
| + | |||
| + | [[Ejemplo de bomba de calor de Carnot|'''Solución''']] | ||
| + | |||
| + | ===[[Producción de entropía en un frigorífico real]]=== | ||
| + | |||
| + | Para mantener su interior a 4°C en una habitación que se encuentra a 27°C un frigorífico ha de extraer 360 kJ/min de su interior. Si la entrada de potencia requerida por el frigorífico es 2 kW, determine: | ||
| + | |||
| + | # Eficiencia del refrigerador. Compárela con la eficiencia de un refrigerador ideal (reversible) que trabaje entre los mismos focos térmicos. | ||
| + | # Potencia extra que consume este frigorífico respecto a uno ideal que extraiga la misma energía de su interior. | ||
| + | # Entropía generada por segundo en el universo por la operación del frigorífico real. | ||
| + | |||
| + | [[Producción de entropía en un frigorífico real|'''Solución''']] | ||
| + | |||
| + | ===[[Ciclo con un proceso reversible y otro irreversible]]=== | ||
| + | Un mol de un gas ideal sufre en primer lugar una expansión libre desde <math>V_1=12.4\,\mathrm{l}</math> y | ||
| + | <math>T_1=300\,\mathrm{K}</math> hasta <math>V_2=24.6\,\mathrm{l}</math> y <math>T_1=300\,\mathrm{K}</math>. | ||
| + | Luego se comprime isoterma y cuasiestáticamente, volviendo a sus estado original. | ||
| + | |||
| + | #¿Cuál es la variación de entropía del Universo en el ciclo completo? | ||
| + | #¿Cuanto trabajo se desperdicia en este ciclo? | ||
| + | #Demuestre que este trabajo perdido es <math>T\Delta S_u</math>. | ||
| + | |||
| + | [[Ciclo con un proceso reversible y otro irreversible|'''Solución''']] | ||
| + | |||
| + | ===[[Compresión adiabática irreversible]]=== | ||
| + | Se tiene un cilindro de paredes adiabáticas cerrado por un pistón móvil, también adiabático. En el interior del cilindro se encuentra un gas ideal sitiado inicialmente a una presión <math>p_0</math>, una temperatura <math>T_0</math> y ocupando un volumen <math>V_0</math>. De pronto se aumenta bruscamente la presión externa colocando una pesa sobre el pistón, de forma que la nueva presión externa pasa a ser <math>p_1=rp_0 >p_0</math>. El gas se comprime hasta que las presiones interna y externa vuelven a coincidir. | ||
| + | |||
| + | # Halle la temperatura final y el volumen final ocupado por el gas. | ||
| + | # Calcule el incremento de entropía del sistema | ||
| + | # Supongamos que se trata de un gas diatómico a una presión inicial de 1 atm, una temperatura inicial 20°C y un volumen inicial de 100 cm³. Si la presión final es de 2 atm. ¿Cuál es el volumen y la temperatura finales, el trabajo realizado sobre el sistema y el aumento de entropía? Compárense estos resultados con lo que se obtienen en una compresión adiabática reversible desde 1 a 2 atm. | ||
| + | |||
| + | [[Compresión adiabática irreversible|'''Solución''']] | ||
| + | |||
| + | ===[[Entropía de una mezcla de gases]]=== | ||
| + | Un recipiente de 2.00 l tiene una barrera que lo divide por la mitad. Una mitad contiene H<sub>2</sub> y la otra O<sub>2</sub>. Ambos gases se encuentran a temperatura ambiente y presión atmosférica. Se retira la barrera de separación, permitiendo que los gases se mezclen. ¿Cuál el aumento de entropía del sistema? | ||
| + | |||
| + | [[Entropía de una mezcla de gases|'''Solución''']] | ||
| + | |||
| + | |||
| + | ===[[Transferencia reversible de calor]]=== | ||
| + | Se tienen dos recipientes adiabáticos conteniendo 500 g de agua cada uno, a 0°C y 100°C, respectivamente. | ||
| + | |||
| + | # Se ponen en contacto a través de una pared diaterma. Halle: | ||
| + | ## La temperatura final del agua. | ||
| + | ## La cantidad de calor transferida. | ||
| + | ## La variación de entropía en el proceso. | ||
| + | # Suponga ahora que el contacto térmico no se hace directamente sino a través de una máquina térmica reversible que usa los recipientes como foco caliente y foco frío. Teniendo en cuenta que todos los procesos son reversibles | ||
| + | ## Halle la temperatura final del agua | ||
| + | ## Calcule el calor cedido por el agua caliente y el absorbido por el agua fría | ||
| + | ## Determine el trabajo que se puede extraer del sistema. | ||
| + | |||
| + | [[Transferencia reversible de calor|'''Solución''']] | ||
| + | |||
| + | ===[[Caso extremo de ciclo Diesel]]=== | ||
| + | [[Imagen:diesel-limite-esquema.png|right]]Una máquina térmica funciona funciona con aire (gas ideal) según el siguiente proceso: | ||
| + | |||
| + | * El gas contenido en una cámara se comprime adiabáticamente de forma reversible desde un volumen máximo <math>V_A</math> hasta un volumen <math>V_B</math>, siendo la razón de compresión <math>r = V_A/V_B</math>. | ||
| + | * A partir de ahí, el gas se pone en contacto con un foco térmico y se calienta a presión constante hasta un estado C, cuyo volumen es igual al inicial. | ||
| + | * Acto seguido, el gas se enfría a volumen constante hasta que la temperatura retorna a su valor inicial. | ||
| + | |||
| + | # Halle el calor absorbido y cedido por el gas durante el ciclo, así como el trabajo realizado sobre el sistema. Demuestre que el rendimiento de este ciclo es igual a | ||
| + | |||
| + | <center><math>\eta = 1 - \frac{r^\gamma-1}{\gamma r^{\gamma-1}(r-1)}</math></center> | ||
| + | <ol start="2"> | ||
| + | <li> Para el caso concreto de aire con <math>p_A=100\,\mathrm{kPa}</math>, <math>t_A=17^\circ\mathrm{C}</math>, <math>V_A=1900\,\mathrm{cm}^3</math> y <math>r=3</math>, ¿cuánto valen las temperaturas y presiones en B y C? ¿Y el calor absorbido, el cedido y el trabajo realizado? ¿Y el rendimiento? </li> | ||
| + | <li> Supongamos que el calentamiento se produce a base de poner en contacto el gas con un foco a temperatura constante <math>T_C</math>, y el enfriamiento mediante el contacto con el ambiente a <math>T_A</math>. ¿Cuánto vale la variación de entropía en el sistema y en el universo en cada paso? ¿Cuál es la variación neta de entropía del universo?</li> | ||
| + | <li> ¿Cuánto vale el trabajo perdido en este ciclo si lo comparamos con el máximo posible para el mismo calor absorbido con las | ||
| + | temperaturas de trabajo <math>T_A</math> y <math>T_C</math>?</li> | ||
| + | </ol> | ||
| + | |||
| + | ===[[Exergía de un volumen de aire comprimido en un tanque]]=== | ||
| + | Un tanque de 200 m<sup>3</sup> de volumen contiene aire a una presión de 1 MPa y temperatura de 300 K. Determine que cantidad máxima de trabajo puede obtenerse de él si las condiciones del entorno son P<sub>0</sub>=100 kPa y T<sub>0</sub>=300 K. | ||
| + | |||
| + | [[Exergía de un volumen de aire comprimido en un tanque|'''Solución''']] | ||
[[Categoría:Problemas del segundo principio de la termodinámica|0]] | [[Categoría:Problemas del segundo principio de la termodinámica|0]] | ||
[[Categoría:Segundo Principio]] | [[Categoría:Segundo Principio]] | ||
[[Categoría:Problemas de Física Aeronáuticos]] | [[Categoría:Problemas de Física Aeronáuticos]] | ||
última version al 11:48 7 sep 2010
1 Ejemplo de máquina térmica
Una máquina térmica consume 240 kg de carbón por hora, siendo el poder calorífico de este combustible de 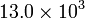 kcal/kg. Si la máquina tiene un rendimiento del 25% calcule el trabajo suministrado por la máquina y el calor cedido al foco frío en una hora
kcal/kg. Si la máquina tiene un rendimiento del 25% calcule el trabajo suministrado por la máquina y el calor cedido al foco frío en una hora
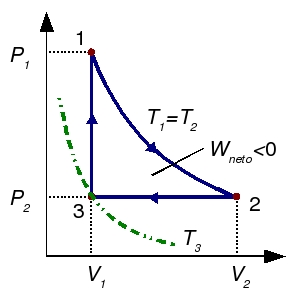
2 Rendimiento de un ciclo recorrido por un gas ideal
Un gas ideal diatómico recorre el siguiente ciclo: partiendo del el estado de coordenadas, 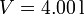 ,
, 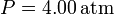 ,
, 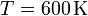 , se dilata isotérmicamente hasta duplicar su volumen. Después se comprime a presión constante hasta su volumen inicial. Finalmente se calienta a volumen constante hasta que alcanza la presión original. Calcule el rendimiento del ciclo.
, se dilata isotérmicamente hasta duplicar su volumen. Después se comprime a presión constante hasta su volumen inicial. Finalmente se calienta a volumen constante hasta que alcanza la presión original. Calcule el rendimiento del ciclo.
3 Sobrecoste originado por la luz de un frigorífico
El interruptor de la luz interior de un frigorífico está estropeado, de modo que la luz está siempre encendida. La luz interior consume una potencia de 40.0 W. Si la eficiencia del frigorífico es 1.3, y el coste de la electricidad es de 11.0 céntimos por kWh, calcule el incremento en el consumo del frigorífico y el coste añadido por año si no se arregla el interruptor.
4 Rendimiento de aparatos hipotéticos
Un inventor mantiene que ha desarrollado una máquina térmica que recibe 700 kJ de calor desde un foco térmico a 500 K y produce 300 kJ de trabajo neto transfiriendo el calor sobrante a un foco térmico a 290 K. ¿Es razonable?
Nuestro inventor vuelve a la carga, esta vez con un refrigerador que, asegura, mantiene el espacio refrigerado a 2°C mientras el ambiente se encuentra a 24°C, teniendo una eficiencia de 13.5. ¿Le hacemos caso?
5 Rendimiento de una máquina térmica real
Una máquina térmica que funciona entre 200°C y 80.0°C alcanza un 20.0% de su rendimiento teórico máximo. ¿Cuanta energía debe absorber para realizar 10.0 kJ de trabajo?
6 Ejemplo de frigorífico de Carnot
Una máquina frigorífica de las que se emplean para fabricar hielo funciona segín un ciclo de Carnot reversible absorbiendo calor de un tanque de agua a 0.00°C y cediéndolo al aire en el interior de un local que se mantiene a 26.0°C. La máquina fabrica 223 kg de hielo en un día. Calcule el trabajo consumido y el calor cedido al aire.
7 Rendimiento de un aparato de aire acondicionado
Para refrescar una habitación se emplea un aparato de aire acondicionado con un coeficiente de despeño (COP o η) de 4. El exterior se encuentra a 34°C mientras que el interior del despacho se mantiene a 24°C. El despacho, que esta vacío, tiene una ventana de vidrio por la cual entra calor desde el exterior.
- Si el calor que entra por la ventana en la unidad de tiempo es
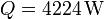 , calcule el trabajo por segundo (potencia) que debe realizar el aparato para mantener la temperatura interior y la cantidad de calor que es arrojada al exterior.
, calcule el trabajo por segundo (potencia) que debe realizar el aparato para mantener la temperatura interior y la cantidad de calor que es arrojada al exterior.
- Determine el COP máximo que podría tener un aparato de aire acondicionado que operara entre estas dos temperaturas.
- Halle la potencia mínima que se requeriría para extraer la misma cantidad de calor por segundo, así como la potencia extra que requiere el aparato real.
- Demuestre que el calor que entra por segundo en la habitación coincide con el valor dado en el primer apartado, si las dimensiones de la ventana son de 5 mm de espesor, 160 cm de ancho y 120 cm de alto. La conductividad calorífica del vidrio es
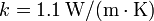 .
.
- Si se sustituye el cristal por uno doble, formado por dos láminas de vidrio como la anterior, entre las cuales hay una capa de aire de 2 cm de espesor, con una conductividad térmica efectiva
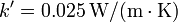 , ¿cómo cambian los resultados anteriores?
, ¿cómo cambian los resultados anteriores?
8 Variación de entropía en el paso de hielo a vapor
Calcule la variación de entropía de un bloque de hielo de 27.0 g a −12.0°C cuando pasa reversiblemente al estado de vapor a 115°C, a presión constante.
Datos: cp (vapor) = 2.08 kJ/kg K, cp (agua) = 4.18 kJ/kg K, cp (hielo) = 2.11 kJ/kg K, Lf = 333.53 J/g, Lv=2257 J/g
9 Inmersión de un bloque metálico en agua
Un bloque de cobre de 50 kg a 80°C se deja caer en un tanque aislado adiabáticamente que contiene 120 l de agua a 25°C. Determine la temperatura final de equilibrio y la variación total del entropía.
Dato: cp(cobre) = 0.095 cal/g·K.
10 Comparación de dos variaciones de entropía
Calcule la variación de entropía en las dos situaciones siguientes:
- 100 ml de agua a 80°C son vertidos en un tanque de agua a 20°C.
- 100 ml de agua a 20°C son vertidos en un tanque de agua a 80°C.
Suponga que la presión es la atmosférica en todo momento.
11 Variación de entropía con un baño térmico
Un tanque de volumen constante contiene 100 moles de aire a una presión de 100 kPa y una temperatura de 327°C. El aire se enfría hasta la temperatura del ambiente de 27.0°C. Suponiendo que el aire se comporta como un gas ideal diatómico, determine la variación de entropía del aire y del Universo durante el proceso.
12 Fusión de hielo en un recipiente
Se tiene un bloque de hielo de masa 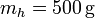 de hielo sumergido en un volumen de agua de masa
de hielo sumergido en un volumen de agua de masa 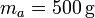 , ambos a una temperatura
, ambos a una temperatura 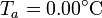 . El conjunto está contenido en un recipiente
cilíndrico de vidrio, de diámetro
. El conjunto está contenido en un recipiente
cilíndrico de vidrio, de diámetro 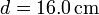 y espesor
y espesor 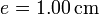 , abierto por arriba al aire (que se puede suponer un aislante térmico perfecto). El recipiente está sumergido en un baño de agua a
, abierto por arriba al aire (que se puede suponer un aislante térmico perfecto). El recipiente está sumergido en un baño de agua a 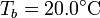 .
.
- Calcula la superficie de agua en contacto con el recipiente y la cantidad de calor que entra en él en 1.00 s.
- Halla la cantidad de hielo que se funde en el mismo tiempo. ¿Cuánto tiempo tardará en derretirse por completo?
- Calcula la variación de entropía en el sistema, en el ambiente y la variación de entropía total en la fusión completa del hielo.
- Supón que en lugar de permitir que el calor fluya directamente desde el baño al sistema se hace pasar por una máquina térmica reversible que opera entre las dos temperaturas. ¿Qué trabajo puede producirse hasta que el hielo se funde completamente? ¿Cuánto calor sale del baño en ese caso? Calcula la variación de entropía del Universo en este proceso.
Datos: Densidad de masa del agua líquida 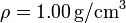 ; Conductividad térmica del vidrio
; Conductividad térmica del vidrio 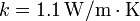 ; Entalpía específica de fusión:
; Entalpía específica de fusión: 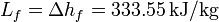
13 Refrigerador alimentado por una máquina térmica
Un refrigerador que funciona entre una temperatura de -23 °C y la temperatura ambiente de 27 °C posee un coeficiente de desempeño de 3. Para hacer funcionar este refrigerador se emplea una máquina térmica que funciona entre 227 °C y la misma temperatura ambiente, la cual tiene un rendimiento de 0.2. Todo el trabajo producido por la máquina térmica se emplea en hacer funcionar el refrigerador.
- Definimos la eficiencia del conjunto máquina más refrigerador como el calor extraído del foco frío dividido por el calor que es necesario extraer del foco caliente, ¿cuál es la eficiencia del conjunto?
- Si se necesitan extraer 100 J por segundo del foco frío, ¿cuánto calor hay que extraer del foco caliente para hacer funcionar el sistema? ¿Cuánto trabajo realiza en la unidad de tiempo la máquina sobre el refrigerador?
- Calcule la producción de entropía en la unidad de tiempo debida a este conjunto.
- Si tanto el refrigerador como la máquina térmica fueran máquinas de Carnot, ¿cuál sería la eficiencia máxima del conjunto? ¿Qué calor sería necesario sacar del foco caliente en ese caso para extraer 100 J/s del foco frío?
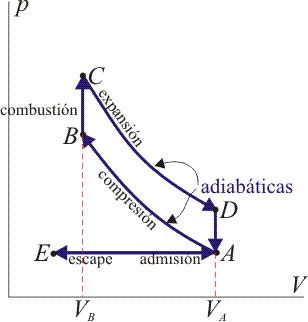
14 Eficiencia de un ciclo Otto
Un ciclo Otto ideal modela el comportamiento de un motor de explosión. Este ciclo está formado por seis pasos, según seindica en la figura. Pruebe que el rendimiento de este ciclo viene dado por la expresión
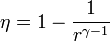
siendo r = VA / VB la razón de compresión igual al cociente entre el volumen al inicio del ciclo de compresión y al final de él. Para ello, halle el rendimiento a partir del calor que entra en el sistema y el que sale de él; exprese el resultado en términos de las temperaturas en los vértices del ciclo y, con ayuda de la ley de Poisson, relacione este resultado con los volúmenes VA y VB.
15 Caso práctico de ciclo Otto
Suponga un ciclo Otto ideal con una relación de compresión de 8. Al inicio de la fase de compresión, el aire está a 100 kPa y 17°C. En la combustión se añaden 800 kJ/kg de calor. Determine la temperatura y la presión máximas que se producen en el ciclo, la salida de trabajo neto y el rendimiento de este motor.
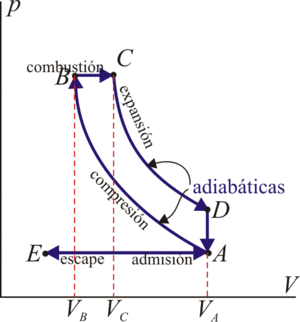
16 Eficiencia de un ciclo Diesel
Un motor diésel puede modelarse con el ciclo ideal formado por seis pasos reversibles, según se indica en la figura. Pruebe que el rendimiento de este ciclo viene dado por la expresión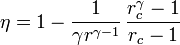
siendo r = VA / VB la razón de compresión y rc = VC / VB la relación de combustión. El método para obtener este resultado es análogo al empleado para el ciclo Otto. Compare los rendimientos del ciclo de Otto y el diésel. ¿Cuáles son las ventajas e inconvenientes respectivos?
17 Caso práctico de ciclo Diesel
Suponga un motor diésel con una capacidad máxima de 1900 cm³. aEn este motor el aire a la entrada está a una presión de 1 atm y una temperatura de 17°C. Si para este motor la razón de compresión es 18 y la de combustión vale 2, determine los volúmenes, presiones y temperaturas de cada vértice del ciclo, así como su rendimiento y el calor y el trabajo intercambiados por el motor.
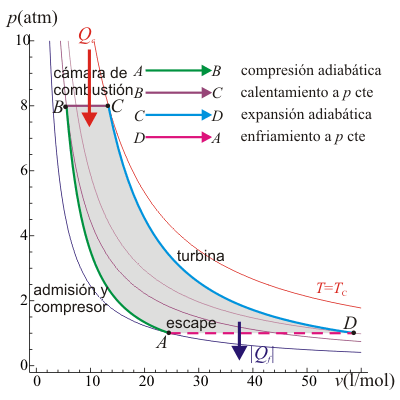
18 Eficiencia de un ciclo Brayton
Un ciclo Brayton (o Joule) ideal modela el comportamiento de una turbina, como las empleadas en las aeronaves. Este ciclo está formado por cuatro pasos reversibles, según se indica en la figura. Pruebe que el rendimiento de este ciclo viene dado por la expresión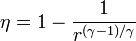
siendo r = pB / pA la relación de presión igual al cociente entre la presión al final del proceso de compresión y al inicio de él. El método para obtener este resultado es análogo al empleado para el ciclo Otto.
19 Caso práctico de ciclo Brayton
Una central eléctrica de turbina de gas que opera en un ciclo Brayton ideal tiene una relación de presión de 8. La temperatura del gas es de 300 K en la entrada del compresor y de 1300 K en la entrada de la turbina. Determine la temperatura del gas a la salida del compresor y de la turbina, y la eficiencia de esta turbina.
20 Caso práctico de ciclo de Stirling
100 moles de gas ideal diátomico sufre un ciclo de Stirling internamente reversible, representado en la figura. El ciclo se compone de dos isotermas y dos isócoras. Las temperaturas de trabajo son 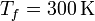 y
y 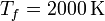 , mientras que las presiones extremas son
, mientras que las presiones extremas son 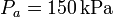 y
y 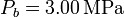 .
.
- En cada uno de los procesos, calcula la variación de energía interna, el trabajo realizado y el calor absorbido por el gas. Calcula el rendimiento del ciclo.
- Calcula la variación de entropía en cada proceso del ciclo y la variación neta en el ciclo completo.
- Compara el rendimiento del ciclo con el de una máquina de Carnot reversible que trabaje entre las mismas temperaturas.
- Imagina y describe un experimento que te permita recorrer el ciclo.
Dato: 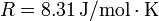
21 Máximo aprovechamiento del calor
Suponga que se tiene un bloque de 10 kg de hierro (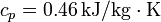 ) a una temperatura de 200°C y se quiere usar para caldear una gran habitación a una temperatura
) a una temperatura de 200°C y se quiere usar para caldear una gran habitación a una temperatura 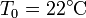 , estando el exterior a 5°C.
, estando el exterior a 5°C.
- Si se coloca el bloque directamente en la habitación, calcule el calor que libera al ambiente.
- Halle la variación de entropía del bloque y del universo en el caso anterior.
- El calor del bloque puede aprovecharse para producir algún trabajo. Para ello, suponga que cuando el bloque se encuentra a una temperatura T, y libera una cantidad de calor
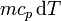 , dicho calor se hace pasar por una máquina reversible que opera entre la temperatura T y la del ambiente. Calcule el trabajo obtenible en este paso y la cantitad total de trabajo que se podría obtener.
, dicho calor se hace pasar por una máquina reversible que opera entre la temperatura T y la del ambiente. Calcule el trabajo obtenible en este paso y la cantitad total de trabajo que se podría obtener.
- Compruebe que el trabajo perdido es igual a T0ΔSu
- Si ese trabajo se aprovechara para hacer funcionar una bomba de calor reversible que operara entre el exterior y la habitación, ¿cuánto sería el calor total que se liberaría en la habitación?
22 Contacto reversible entre dos recipientes
Se tienen dos recipientes adiabáticos que contienen 400 y 600 g de agua líquida, respectivamente. La temperatura del primer recipiente es de 0.00 °C y la del segundo 100 °C.
- Los dos recipientes se ponen en contacto térmico a través e una pared diaterma. calcula:
- La temperatura final del agua.
- Las cantidades de calor transferidas en el proceso.
- La variación de entropía en el Universo.
- Supón ahora que el contacto térmico no se hace poniendo los sistemas en contacto, sino a través de una máquina térmica reversible que usa los recipientes como foco caliente y frío, de modo que sus temperaturas van cambiando en el tiempo. Si todos los procesos son reversibles…
- Calcula la temperatura final del agua en este caso.
- Calcula el calor cedido por el agua caliente y el absorbido por el agua fría.
- Determina la cantidad de trabajo que se puede extraer del sistema con este procedimiento.
23 Otros problemas
23.1 Ejemplo de bomba de calor de Carnot
Una bomba de calor se emplea para mantener caliente una vivienda que se encuentra a 20.0°C siendo la temperatura exterior -5.00°C. Suponiendo que la bomba de calor es una máquina de Carnot invertida, calcule cuantos julios de energía procedentes del medio ambiente exterior serán transferidos al interior de la vivienda por cada julio de energía eléctrica consumida. Explique las ventajas e incovenientes de este sistema de calefacción frente a uno convencional de disipación de energía en una resistencia eléctrica.
23.2 Producción de entropía en un frigorífico real
Para mantener su interior a 4°C en una habitación que se encuentra a 27°C un frigorífico ha de extraer 360 kJ/min de su interior. Si la entrada de potencia requerida por el frigorífico es 2 kW, determine:
- Eficiencia del refrigerador. Compárela con la eficiencia de un refrigerador ideal (reversible) que trabaje entre los mismos focos térmicos.
- Potencia extra que consume este frigorífico respecto a uno ideal que extraiga la misma energía de su interior.
- Entropía generada por segundo en el universo por la operación del frigorífico real.
23.3 Ciclo con un proceso reversible y otro irreversible
Un mol de un gas ideal sufre en primer lugar una expansión libre desde 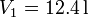 y
y
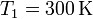 hasta
hasta 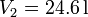 y
y 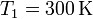 .
Luego se comprime isoterma y cuasiestáticamente, volviendo a sus estado original.
.
Luego se comprime isoterma y cuasiestáticamente, volviendo a sus estado original.
- ¿Cuál es la variación de entropía del Universo en el ciclo completo?
- ¿Cuanto trabajo se desperdicia en este ciclo?
- Demuestre que este trabajo perdido es TΔSu.
23.4 Compresión adiabática irreversible
Se tiene un cilindro de paredes adiabáticas cerrado por un pistón móvil, también adiabático. En el interior del cilindro se encuentra un gas ideal sitiado inicialmente a una presión p0, una temperatura T0 y ocupando un volumen V0. De pronto se aumenta bruscamente la presión externa colocando una pesa sobre el pistón, de forma que la nueva presión externa pasa a ser p1 = rp0 > p0. El gas se comprime hasta que las presiones interna y externa vuelven a coincidir.
- Halle la temperatura final y el volumen final ocupado por el gas.
- Calcule el incremento de entropía del sistema
- Supongamos que se trata de un gas diatómico a una presión inicial de 1 atm, una temperatura inicial 20°C y un volumen inicial de 100 cm³. Si la presión final es de 2 atm. ¿Cuál es el volumen y la temperatura finales, el trabajo realizado sobre el sistema y el aumento de entropía? Compárense estos resultados con lo que se obtienen en una compresión adiabática reversible desde 1 a 2 atm.
23.5 Entropía de una mezcla de gases
Un recipiente de 2.00 l tiene una barrera que lo divide por la mitad. Una mitad contiene H2 y la otra O2. Ambos gases se encuentran a temperatura ambiente y presión atmosférica. Se retira la barrera de separación, permitiendo que los gases se mezclen. ¿Cuál el aumento de entropía del sistema?
23.6 Transferencia reversible de calor
Se tienen dos recipientes adiabáticos conteniendo 500 g de agua cada uno, a 0°C y 100°C, respectivamente.
- Se ponen en contacto a través de una pared diaterma. Halle:
- La temperatura final del agua.
- La cantidad de calor transferida.
- La variación de entropía en el proceso.
- Suponga ahora que el contacto térmico no se hace directamente sino a través de una máquina térmica reversible que usa los recipientes como foco caliente y foco frío. Teniendo en cuenta que todos los procesos son reversibles
- Halle la temperatura final del agua
- Calcule el calor cedido por el agua caliente y el absorbido por el agua fría
- Determine el trabajo que se puede extraer del sistema.
23.7 Caso extremo de ciclo Diesel
Una máquina térmica funciona funciona con aire (gas ideal) según el siguiente proceso:- El gas contenido en una cámara se comprime adiabáticamente de forma reversible desde un volumen máximo VA hasta un volumen VB, siendo la razón de compresión r = VA / VB.
- A partir de ahí, el gas se pone en contacto con un foco térmico y se calienta a presión constante hasta un estado C, cuyo volumen es igual al inicial.
- Acto seguido, el gas se enfría a volumen constante hasta que la temperatura retorna a su valor inicial.
- Halle el calor absorbido y cedido por el gas durante el ciclo, así como el trabajo realizado sobre el sistema. Demuestre que el rendimiento de este ciclo es igual a
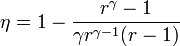
- Para el caso concreto de aire con
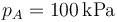 ,
, 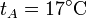 ,
, 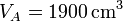 y r = 3, ¿cuánto valen las temperaturas y presiones en B y C? ¿Y el calor absorbido, el cedido y el trabajo realizado? ¿Y el rendimiento?
y r = 3, ¿cuánto valen las temperaturas y presiones en B y C? ¿Y el calor absorbido, el cedido y el trabajo realizado? ¿Y el rendimiento? - Supongamos que el calentamiento se produce a base de poner en contacto el gas con un foco a temperatura constante TC, y el enfriamiento mediante el contacto con el ambiente a TA. ¿Cuánto vale la variación de entropía en el sistema y en el universo en cada paso? ¿Cuál es la variación neta de entropía del universo?
- ¿Cuánto vale el trabajo perdido en este ciclo si lo comparamos con el máximo posible para el mismo calor absorbido con las temperaturas de trabajo TA y TC?
23.8 Exergía de un volumen de aire comprimido en un tanque
Un tanque de 200 m3 de volumen contiene aire a una presión de 1 MPa y temperatura de 300 K. Determine que cantidad máxima de trabajo puede obtenerse de él si las condiciones del entorno son P0=100 kPa y T0=300 K.