Variación de entropía con un baño térmico

De Laplace

1 Enunciado

Un tanque de volumen constante contiene 100 moles de aire a una presión de 100 kPa y una temperatura de 327°C. El aire se enfría hasta la temperatura del ambiente de 27.0°C. Suponiendo que el aire se comporta como un gas ideal diatómico, determine la variación de entropía del aire y del Universo durante el proceso.

2 Variación de entropía del ambiente

Cuando el aire se enfría intercambia una cierta cantidad de calor igual a

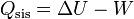
Puesto que el proceso ocurre a volumen constante, el trabajo realizado sobre el gas es nulo y el calor equivale a la variación de la energía interna

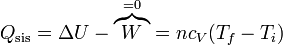
cuyo valor es

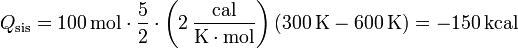
Este calor es negativo pues en realidad sale del sistema

El calor que entra en el ambiente es este mismo, cambiado de signo

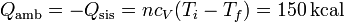
Esta entrada de calor se produce a una temperatura constante (en el ambiente), por lo que el aumento de entropía del ambiente es

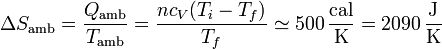
Un cálculo más preciso, usando los valores empíricos de la capacidad calorífica del aire da

3 Variación de entropía del sistema

El proceso que se describe en este ejemplo es irreversible, ya que se debe a una cesión de calor debida a una diferencia finita de temperaturas. En el gas, el enfriamiento se producirá en general de una forma complicada, enfriándose primero las partes en contacto con las paredes y luego, por conducción, difusión o radiación, las partes del interior. Sin embargo, al ser tanto el estado inicial como el final estados de equilibrio, podemos calcular la variación de entropía suponiendo un proceso reversible que conecte estos dos mismos estados.

Este proceso reversible sería una variación gradual y uniforme de la temperatura, de forma que en todo momento el gas se supone en equilibrio térmico. Para realizar este proceso necesitaríamos una cantidad infinita de baños térmicos, cada uno a una temperatura ligeramente superior al siguiente, de forma que situaríamos al gas en contacto sucesivo con cada uno de ellos. Por supuesto, este proceso es irrealizable en la práctica, pero nos basta para hallar el cambio de entropía.

La variación de entropía cuando el gas pasa de una temperatura T a una T + dT es

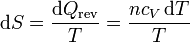
Si suponemos que la capacidad calorífica no depende de la temperatura, podemos integrar esta ecuación y obtener el incremento de entropía

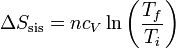
Sustituyendo nos queda

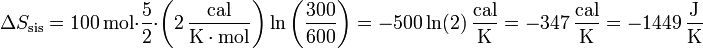
La variación es negativa porque al enfriarse el sistema reduce su agitación térmica, ordenándose y disminuyendo su entropía.

De nuevo, un cálculo más exacto usando 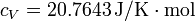, da

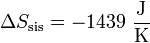
4 Variación de entropía total

Sumando las dos contribuciones obtenemos la variación de entropía total del universo.

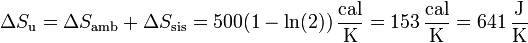
(0, más exactamente, 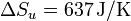). La variación neta es positiva pues estamos considerando un proceso irreversible.