Rendimiento de un ciclo recorrido por un gas ideal

De Laplace

Contenido

1 Enunciado
2 Diagrama
3 Proceso isotermo 1→2
4 Proceso isobaro 2→3
5 Proceso isócoro 3→1
6 Rendimiento del ciclo
7 Comparación con una máquina de Carnot

1 Enunciado

Un gas ideal diatómico recorre el siguiente ciclo: partiendo del el estado de coordenadas, 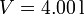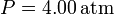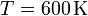$V = 4.00 \,\mathrm{l}$ , $P = 4.00\,\mathrm{atm}$ , $T = 600\,\mathrm{K}$ , se dilata isotérmicamente hasta duplicar su volumen. Después se comprime a presión constante hasta su volumen inicial. Finalmente se calienta a volumen constante hasta que alcanza la presión original. Calcule el rendimiento del ciclo.

2 Diagrama

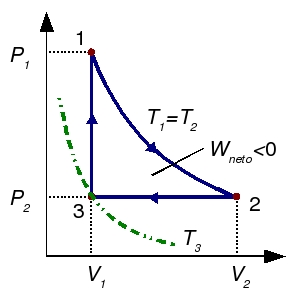
La figura muestra el ciclo en el diagrama $P V$ . El rendimiento del ciclo es el trabajo neto obtenido dividido por el calor suministrado al gas. Vamos a calcular el trabajo y el calor absorbido en cada fase del ciclo

3 Proceso isotermo 1→2

Los datos de los estados inicial y final son

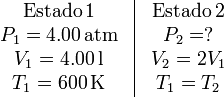
$\begin{array}{c|c} \begin{array}{c} \mathrm{Estado\,1}\\ P_1=4.00\,\mathrm{atm}\\ V_1=4.00\,\mathrm{l}\\ T_1=600\,\mathrm{K} \end{array}& \begin{array}{c} \mathrm{Estado\,2}\\ P_2=?\\ V_2=2V_1\\ T_1=T_2 \end{array} \end{array}$

El trabajo realizado por una gas ideal en un proceso isotermo es

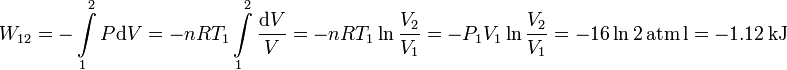
$W_{12}=-\int\limits_1^2P\mathrm{d} V=-nRT_1\int\limits_1^2\frac{\mathrm{d} V}{V}=-nRT_1\ln\frac{V_2}{V_1}= -P_1V_1\ln\frac{V_2}{V_1}=-16\ln2\,\mathrm{atm\,l}=-1.12\,\mathrm{kJ}$

Como el proceso es isotermo, la variación de energía interna es nula. Entonces

$Q_{12}=\Delta U_{12}-W_{12}=-W_{12}=1.12\,\mathrm{kJ}$

El trabajo es negativo, lo realiza el gas sobre el entorno, y el calor es positivo, es suministrado al gas.

4 Proceso isobaro 2→3

En este caso, los datos de los procesos son

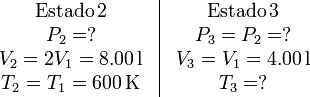
$\begin{array}{c|c} \begin{array}{c} \mathrm{Estado\,2}\\ P_2=?\\ V_2=2V_1=8.00\,\mathrm{l}\\ T_2=T_1=600\,\mathrm{K} \end{array}& \begin{array}{c} \mathrm{Estado\,3}\\ P_3=P_2=?\\ V_3=V_1=4.00\,\mathrm{l}\\ T_3=? \end{array} \end{array}$

El trabajo realizado en este proceso es

$W 23 = - P 2 (V 3 - V 2) = - P 2 (V 1 - V 2) = P 2 V 1$

Necesitamos el valor de $P 2$ . Para ello aplicamos la ley de Boyle entre los estados 1 y 2

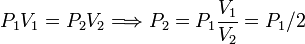
$P_1V_1=P_2V_2\Longrightarrow P_2=P_1\frac{V_1}{V_2}=P_1/2$

Por tanto el trabajo es

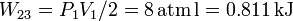
$W_{23}=P_1V_1/2=8\,\mathrm{atm\,l}=0.811\,\mathrm{kJ}$

Al ser el proceso isobaro, el calor absorbido por el gas es

$Q 23 = n c p (T 3 - T 2)$

El enunciado dice que el gas es diatómico. Entonces $c p = 7 R / 2$ . Para averiguar $T 3$ relacionamos los estados 2 y 3 con la ecuación de estado del gas ideal

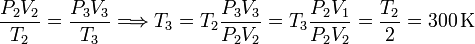
$\frac{P_2V_2}{T_2}=\frac{P_3V_3}{T_3}\Longrightarrow T_3=T_2\frac{P_3V_3}{P_2V_2}= T_3\frac{P_2V_1}{P_2V_2}=\frac{T_2}{2}=300\,\mathrm{K}$

El calor es

$Q_{23}=\frac{7}{2}nR\left(\frac{T_2}{2}-T_2\right)= -\frac{7}{4}nRT_2=-\frac{7}{4}P_2V_2=-\frac{7}{4}P_1V_1=-28\,\mathrm{atm\,l}=-2.84\,\mathrm{kJ}$

En este caso el trabajo contribuye se realiza sobre el gas, mientras que el gas cede el calor al entorno.

5 Proceso isócoro 3→1

Aquí no hay variación de volumen, por lo que el trabajo es nulo

$W 31 = 0$

Como el gas es diatómico, $c v = 5 R / 2$ . Entonces, el calor transferido es

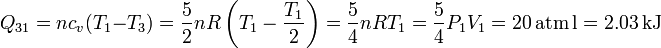
$Q_{31}=nc_v(T_1-T_3)=\frac{5}{2}nR\left(T_1-\frac{T_1}{2}\right)=\frac{5}{4}nRT_1=\frac{5}{4}P_1V_1=20\,\mathrm{atm\,l}=2.03\,\mathrm{kJ}$

Al ser positivo, este calor es absorbido por el gas.

6 Rendimiento del ciclo

En el rendimiento debemos comparar el trabajo neto proporcionado por el gas y el calor total suministrado. De los apartados anteriores tenemos

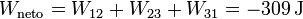
$W_{\mathrm{neto}}=W_{12}+W_{23}+W_{31}=-309\,\mathrm{J}$

y

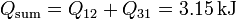
$Q_{\mathrm{sum}}=Q_{12}+Q_{31}=3.15\,\mathrm{kJ}$

Entonces el rendimiento es

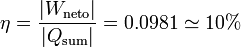
$\eta = \frac{|W_{\mathrm{neto}}|}{|Q_{\mathrm{sum}}|}=0.0981\simeq10%$

Podemos verificar que el resultado es razonable usando que, como el proceso es cíclico, la variación total de energía interna debe ser nulo, esto es, debe cumpplirse

$W 12 + W 23 + W 31 = - (Q 12 + Q 23 + Q 31)$

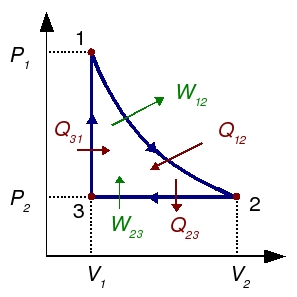
En el diagrama se han añadido los calores y trabajos realizados indicando cómo contribuyen a la variación de energía interna del gas.

7 Comparación con una máquina de Carnot

Podemos comparar el rendimiento obtenido en este ciclo con el que proporcionaría una máquina de Carnot trabajando entre las temperaturas extremas alcanzadas en el ciclo, $T 1$ y $T 3$ . Tenemos

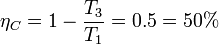
$\eta_C=1-\frac{T_3}{T_1}=0.5=50%$

Así pues, el ciclo del enunciado proporciona un rendimiento que es el 20% del máximo que se puede alcanzar trabajando entre estas temperaturas.

Rendimiento de un ciclo recorrido por un gas ideal

De Laplace

Contenido

1 Enunciado

2 Diagrama

3 Proceso isotermo 1→2

4 Proceso isobaro 2→3

5 Proceso isócoro 3→1

6 Rendimiento del ciclo

7 Comparación con una máquina de Carnot

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES