Ciclo con un proceso reversible y otro irreversible

De Laplace

Contenido

1 Enunciado
2 Variación de entropía del Universo
3 Trabajo desperdiciado
4 Relación entre el trabajo perdido y la variación de entropía

1 Enunciado

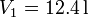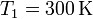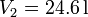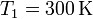Un mol de un gas ideal sufre en primer lugar una expansión libre desde $V_1=12.4\,\mathrm{l}$ y $T_1=300\,\mathrm{K}$ hasta $V_2=24.6\,\mathrm{l}$ y $T_1=300\,\mathrm{K}$ . Luego se comprime isoterma y cuasiestáticamente, volviendo a su estado original.

¿Cuál es la variación de entropía del Universo en el ciclo completo?
¿Cuanto trabajo se desperdicia en este ciclo?
Demuestre que este trabajo perdido es $T Δ S u$ .

2 Variación de entropía del Universo

En este problema se nos plantea un sistema que recorre un ciclo, pues el estado final y el estado inicial son el mismo. Este ciclo tiene la particularidad de que tiene una parte irreversible y otra reversible. La parte irreversible es la expansión inicial y la reversible la compresión posterior. Ambos procesos son isotermos. Analicemos cada uno de ellos por separado

2.1 Expansión isoterma irreversible

En este proceso el gas no realiza trabajo, pues la expansión es libre y no empuja ninguna pared o pistón. Como las temperaturas inicial y final son iguales, la variación de energía interna del gas es nula. Entonces el calor absorbido por el gas es

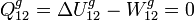
$Q_{12}^g=\Delta U_{12}^g-W_{12}^g=0$

El gas no absorbe calor durante el proceso.

La variación de entropía del gas entre los estados 1 y 2 es

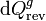$\Delta S_{12}^g=\int\limits_1^2\frac{\mathrm{d}Q_{\mathrm{rev}}^g}{T}$

donde $\mathrm{d}Q_{\mathrm{rev}}^g$ es el calor que el gas absorbe al pasar del estado 1 y 2 a lo largo de un proceso reversible. Como en este proceso el gas no absorbe calor podríamos estar tentados de decir que su entropía no varía. Pero esto no sería correcto, pues la expansión libre es irreversible y no puede usarse para calcular la variación de entropía.

Para poder calcular 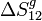$\Delta S_{12}^g$ hemos de imaginar un proceso reversible que una los estados 1 y 2. Como tienen la misma temperatura, este proceso imaginario puede ser una expansión isoterma reversible entre los estados 1 y 2. En este proceso imaginario, la variación de energía interna es nula de nuevo, pero el gas realiza trabajo y absorbe calor de su entorno. De hecho usamos el trabajo que realiza para calcular el calor que absorbe. En cada paso infinitesimal de este proceso tenemos

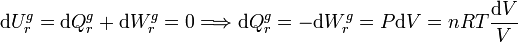
$\mathrm{d}U_r^g=\mathrm{d}Q_r^g+\mathrm{d}W_r^g=0\Longrightarrow \mathrm{d}Q_r^g=-\mathrm{d}W_r^g=P\mathrm{d}V=nRT\frac{\mathrm{d}V}{V}$

En cada uno de estos pasos infinitesimales la variación de entropía es

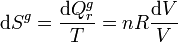
$\mathrm{d}S^g=\frac{\mathrm{d}Q_r^g}{T}=nR\frac{\mathrm{d}V}{V}$

y la variación de entropía total en el proceso es

$\Delta S_{12}^g=\int\limits_1^2\frac{\mathrm{d}Q_r}{T}=\int\limits_1^2nR\frac{\mathrm{d}V}{V}=nR\ln\frac{V_2}{V_1}>0$

EL signo es positivo pues se tiene $V 2 > V 1$ . El gas aumenta su entropía aunque no absorbe calor. Este incremento de entropía proviene de la irreversibilidad del proceso.

La variación del entropía del entorno es 0, pues al no absorber calor del gas ni recibir trabajo de él su estado no se ve alterado. Entonces

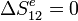
$\Delta S_{12}^e=0$

Y la variación de entropía del Universo es

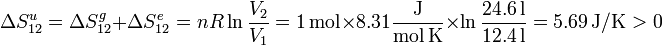
$\Delta S_{12}^u = \Delta S_{12}^g+\Delta S_{12}^e=nR\ln\frac{V_2}{V_1}= 1\,\mathrm{mol}\times8.31\mathrm{\frac{J}{mol\,K}}\times\ln\frac{24.6\,\mathrm{l}}{12.4\,\mathrm{l}}=5.69\,\mathrm{J/K}>0$

La variación total de entropía del Universo es positiva pues el proceso es irreversible.

2.2 Compresión isoterma reversible

La entropía es una función de estado, por lo que la variación entre dos estados no depende del proceso realizado, ya sea reversible o irreversible. Por tanto tenemos

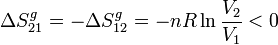
$\Delta S_{21}^g=-\Delta S_{12}^g=-nR\ln\frac{V_2}{V_1}<0$

A diferencia de la expansión irreversible anterior, la variación de entropía proviene del calor cedido por el gas en la compresión isoterma reversible.

Ahora el entorno sí que ve variar su entropía, pues absorbe calor del gas. Este proceso es, de hecho, el inverso del proceso reversible imaginario que hemos usado para calcular la variación de entropía del gas en la expansión irreversible. Así pues, la variación de entropía del entorno en el proceso 21 es

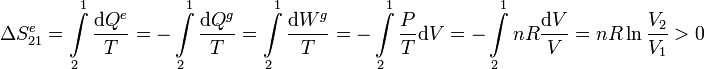
$\Delta S_{21}^e=\int\limits_2^1\frac{\mathrm{d}Q^e}{T}=-\int\limits_2^1\frac{\mathrm{d}Q^g}{T}=\int\limits_2^1\frac{\mathrm{d}W^g}{T}= -\int\limits_2^1\frac{P}{T}\mathrm{d}V= -\int\limits_2^1nR\frac{\mathrm{d}V}{V}=nR\ln\frac{V_2}{V_1}>0$

El aumento de entropía del entorno proviene del calor que absorbe del gas.

Entonces, la variación de entropía del Universo en la compresión es

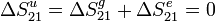
$\Delta S_{21}^u=\Delta S_{21}^g+\Delta S_{21}^e=0$

La variación de entropía del Universo es cero pues el proceso es reversible.

2.3 Balance total de entropía

La variación total de entropía del gas, el entorno y el Universo en el ciclo completo es

$\begin{array}{l} \displaystyle\Delta S^g=\Delta S_{12}^g+\Delta S_{21}^g=0\\ \\ \displaystyle\Delta S^e=\Delta S_{12}^e+\Delta S_{21}^e=nR\ln\frac{V_2}{V_1}=5.69\,\mathrm{J/K}>0\\ \\ \displaystyle\Delta S^u=\Delta S_{12}^u+\Delta S_{21}^u=nR\ln\frac{V_2}{V_1}=5.69\,\mathrm{J/K}>0 \end{array}$

La variación de entropía del sistema en el ciclo es cero, pues el estado inicial y final coinciden. Pero la variación de entropía del Universo es positiva, pues el ciclo contiene procesos irreversibles.

3 Trabajo desperdiciado

En la expansión libre el gas no realiza trabajo. Sin embargo, si la expansión se hubiera hecho de manera reversible, habría realizado un trabajo

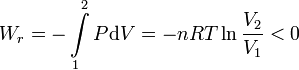
$W_r=-\int\limits_1^2P\mathrm{d}V=-nRT\ln\frac{V_2}{V_1}<0$

El trabajo lo habría hecho sobre el entorno. Es decir, al realizar el proceso de manera completamente irreversible se ha perdido este trabajo. $W r$ representa el trabajo máximo que podríamos sacar de la expansión isoterma del gas, $W max = | W r |$ . Un proceso real en el cual el gas se expande contra un pistón no será completamente reversible, y el trabajo obtenido será menor que $W max$ .

4 Relación entre el trabajo perdido y la variación de entropía

La variación de entropía del Universo puede desglosarse en la variación en cada uno de los procesos

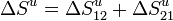
$\Delta S^u=\Delta S_{12}^u + \Delta S_{21}^u$

El proceso 21 es reversible, por lo que 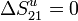$\Delta S_{21}^u=0$ . En el proceso 12 el entorno no se ve alterado, por lo que 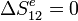$\Delta S_{12}^e=0$ . Por tanto

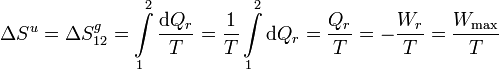
$\Delta S^u=\Delta S_{12}^g=\int\limits_1^2\frac{\mathrm{d}Q_r}{T}=\frac{1}{T}\int\limits_1^2\mathrm{d}Q_r=\frac{Q_r}{T}=-\frac{W_r}{T}= \frac{W_{\mathrm{max}}}{T}$

Por tanto obtenemos

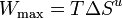
$W_{\mathrm{max}}=T\Delta S^u\,$

Esto nos dice que la irreversibilidad lleva asociada pérdida de trabajo útil, es decir, una degradación de la energía. En general para que un dispositivo sea eficiente hay que diseñarlo de manera que trabaje del modo más reversible posible. Esto quiere decir disminuir el rozamiento, hacer que las transferencias de calor se hagan entre objetos con temperaturas lo mas parecidas posible, etc.

Ciclo con un proceso reversible y otro irreversible

De Laplace

Contenido

1 Enunciado

2 Variación de entropía del Universo

2.1 Expansión isoterma irreversible

2.2 Compresión isoterma reversible

2.3 Balance total de entropía

3 Trabajo desperdiciado

4 Relación entre el trabajo perdido y la variación de entropía

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES