Caso extremo de ciclo Diesel
De Laplace
Contenido |
1 Enunciado
(Segundo Parcial, Junio 2009, P2)
Una máquina térmica funciona funciona con aire (gas ideal) según el siguiente proceso:- El gas contenido en una cámara se comprime adiabáticamente de forma reversible desde un volumen máximo VA hasta un volumen VB, siendo la razón de compresión r = VA / VB.
- A partir de ahí, el gas se pone en contacto con un foco térmico y se calienta a presión constante hasta un estado C, cuyo volumen es igual al inicial.
- Acto seguido, el gas se enfría a volumen constante hasta que la temperatura retorna a su valor inicial.
- Halle el calor absorbido y cedido por el gas durante el ciclo, así como el trabajo realizado sobre el sistema. Demuestre que el rendimiento de este ciclo es igual a
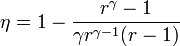
- Para el caso concreto de aire con
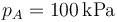 ,
, 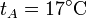 ,
, 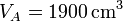 y r = 3, ¿cuánto valen las temperaturas y presiones en B y C? ¿Y el calor absorbido, el cedido y el trabajo realizado? ¿Y el rendimiento?
y r = 3, ¿cuánto valen las temperaturas y presiones en B y C? ¿Y el calor absorbido, el cedido y el trabajo realizado? ¿Y el rendimiento? - Supongamos que el calentamiento se produce a base de poner en contacto el gas con un foco a temperatura constante TC, y el enfriamiento mediante el contacto con el ambiente a TA. ¿Cuánto vale la variación de entropía en el sistema y en el universo en cada paso? ¿Cuál es la variación neta de entropía del universo?
- ¿Cuánto vale el trabajo perdido en este ciclo si lo comparamos con el máximo posible para el mismo calor absorbido con las temperaturas de trabajo TA y TC?
2 Solución compacta
Esto sería la solución en formato resumido.
2.1 Primer apartado
Tenemos tres procesos:
- Compresión adiabática

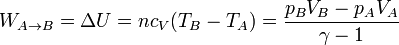
- Calentamiento isóbaro
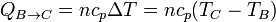
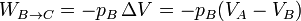
- Enfriamiento isócoro
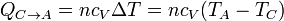
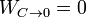
El calor absorbido es 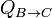 , el cedido
, el cedido 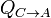 y el trabaja es la suma
y el trabaja es la suma
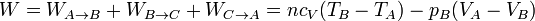
Para hallar el rendimiento aplicamos las relaciones
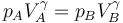

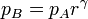

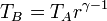
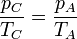

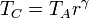
De aquí obtenemos el rendimiento
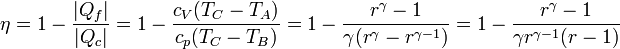
2.2 Segundo apartado
Sustituyendo en las expresiones anteriores obtenemos, para las presiones y temperaturas

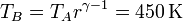

Para los calores y el trabajo


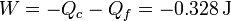
y para el rendimiento
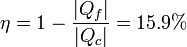
2.3 Tercer apartado
Tenemos tres procesos, y en cada uno tenemos una variación de entropía del sistema y una del ambiente. La del universo será la suma de ambas.
- Compresión adiabática reversible
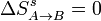
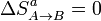

- Calentamiento isóbaro
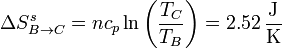

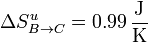
- Enfriamiento isócoro
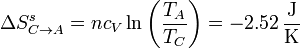
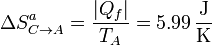

- Variación neta
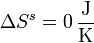
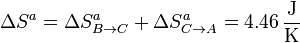
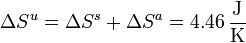
2.4 Cuarto apartado
El rendimiento máximo lo da una máquina de Carnot. Por tanto
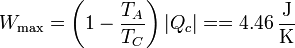
El trabajo perdido es
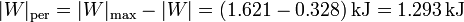
que supone el
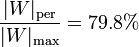
Veamos ahora la solución desarrollada y explicada paso a paso.
3 Calor, trabajo y rendimiento
Para calcular el intercambio energético en cada proceso necesitamos conocer las capacidades caloríficas molares del aire, a presión y a volumen constante. Para ello, no es necesario suponer que el aire es un gas diatómico (aunque aproximadamente se comporta como tal). Conocidos γ (que para el aire vale 1.4) y R (=8.314 J/K·mol) tenemos toda la información necesaria
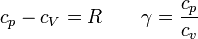

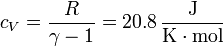
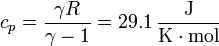
3.1 Calor absorbido
De los tres procesos que tienen lugar en el ciclo en uno de ellos, la compresión adiabática, no se intercambia calor; en otro, el calentamiento isóbara, el sistema absorbe calor, y en el tercero, el enfriamiento isócoro, el sistema cede calor.
Al ser el proceso de calentamiento uno a presión constante entre las temperaturas TB y TC, el calor absorbido es

Alternativamente, podemos escribir esto como
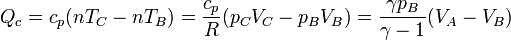
3.2 Calor cedido
El calor se cede en un proceso a volumen constante, entre las temperaturas TC y TA, por lo que vale
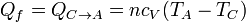
puesto que TA < TC, este calor es negativo, como corresponde a que este calor sale del sistema hacia el ambiente.
Una forma alternativa de este calor es
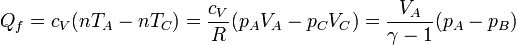
3.3 Trabajo
Podemos calcular el valor neto del trabajo realizado sobre el sistema empleando el Primer Principio de la termodinámica, ya que en un proceso cíclico la energía interna al final es la misma que al principio
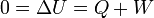


Podemos calcular este valor a partir del trabajo realizado sobre el sistema en cada proceso:
- Compresión adiabática
- En este proceso no se intercambia calor, por lo que el trabajo es igual al incremento de energía interna
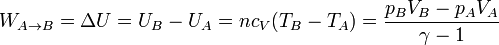
- Calentamiento a presión constante
- El trabajo cuando la presión es constante es igual a esta presión por el incremento de volumen, cambiado de signo
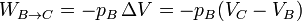
- Podemos poner esto en función de la temperatura, usando la ecuación de los gases ideales
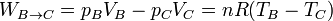
- Este trabajo es negativo ya que en esta expansión es realmente el sistema el que trabaja sobre el ambiente.
- Enfriamiento a volumen constante
- Al no desplazarse las paredes del sistema, aquí no se realiza trabajo mecánico

Sumando las tres contribuciones obtenemos el trabajo total
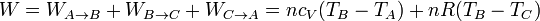
Para ver que este resultado coincide con el que obtuvimos antes, hacemos uso de la ley de Mayer
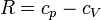

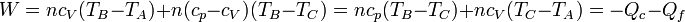
3.4 Rendimiento
3.4.1 A partir de las temperaturas
El rendimiento del ciclo es igual al cociente entre el trabajo neto realizado por el sistema y el calor absorbido durante el ciclo
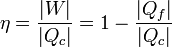
Sustituyendo las expresiones obtenidas anteriormente
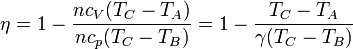
Para expresar el rendimiento en función de la razón de compresión r = VA / VB observamos que, por ser A→B un proceso adiabático tenemos la relación entre temperaturas y volúmenes
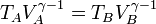

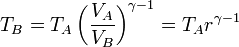
Asimismo, por ser B→C un proceso a presión constante se cumple la ley de Charles
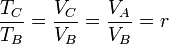

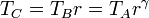
Llevando esto a la expresión del rendimiento
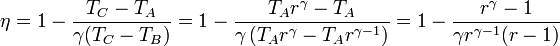
Comparando este resultado con el de un ciclo Diesel vemos que esta expresión es idéntica a la que se obtiene para ese ciclo si hacemos la relación de combustión rc igual a la relación de compresión. En realidad, el ciclo descrito en este problema es en realidad un ciclo Diesel ideal, en el cual una de las adiabáticas se ha reducido a un punto.
3.4.2 A partir de las presiones y volúmenes
Una forma alternativa de obtener este rendimiento consiste en usar las expresiones para los calores en función de las presiones y volúmenes
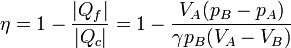
Esta relación solo implica los valores de las magnitudes en los extremos de la adiabática. Estos valores están relacionados por
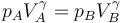

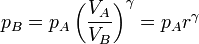
y esto nos da
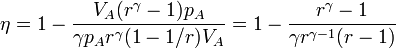
4 Valores numéricos
Se trata ahora de hallar todos los valores anteriores, y algunos más, para un caso particular, con condiciones
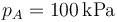
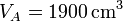
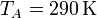
4.1 Presión, volumen y temperatura
El número de moles de gas, que será una constante en el ciclo, lo obtenemos aplicando la ley de los gases ideales
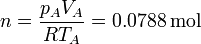
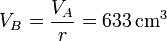

La presión en B (y C) la obtenemos de la ecuación para una adiabática reversible que obtuvimos antes
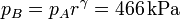
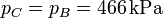
Aquí hemos usado el valor γ = 1.4, propio del aire.
La temperatura en B la hallamos por aplicación de la ley de los gases ideales
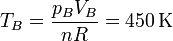
También se puede obtener esta temperatura empleando la relación para un proceso adiabático
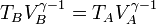

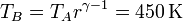
la temperatura en C la obtenemos de la ley de Charles

Alternativamente, puede obtenerse de la temperatura en A empleando la relación que obtuvimos antes
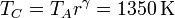
Reuniendo todos estos resultados en una tabla nos queda, en forma analítica
| A | B | C | |
|---|---|---|---|
| p | 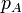
| 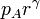
| 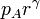
|
| V | 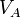
| 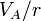
| 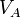
|
| T | 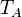
| 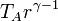
| 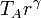
|
y en forma numérica
| A | B | C | |
|---|---|---|---|
| p(kPa) | 100 | 466 | 466 |
| V(cm3) | 1900 | 633 | 1900 |
| T(K) | 290 | 450 | 1350 |
4.2 Calor y trabajo
A partir de aquí, conocidas las temperaturas que calculamos antes, tenemos el calor y el trabajo.
El calor absorbido es

y el calor cedido al ambiente
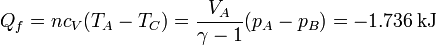
y el trabajo neto es igual al calor total cambiado de signo
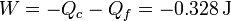
Este resultado, empleando valores absolutos, se escribe
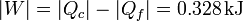
El rendimiento lo podemos hallar a partir de su definición
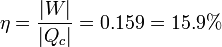
o bien empleando la fórmula dada en el enunciado

5 Entropía
En cada uno de los procesos tenemos la variación de entropía del sistema (que se puede calcular empleando la expresión de la entropía para un gas ideal) y la del ambiente (dado por los focos térmicos). La variación de entropía del universo será la suma de todas ellas.
5.1 Compresión adiabática
En el proceso A→B no hay intercambio de calor con el ambiente, por lo que no cambia la entropía de éste. Como el proceso es además reversible, tampoco cambia la del sistema. Por tanto
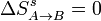
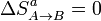

5.2 Calentamiento a presión constante
En el paso B→C, para hallar la variación de la entropía del sistema, empleamos la expresión en términos de la temperatura y la presión

También podríamos haber usado la expresión en función de la temperatura y el volumen, pero de esta forma aprovechamos el que el proceso es a presión constante.
Una forma alternativa de calcular esta variación de entropía es imaginando un proceso reversible que conecte los estados inicial y final. Si suponemos una variación gradual de la temperatura a presión constante
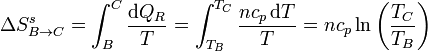
La variación de entropía del ambiente en este proceso la hallamos aplicando que el foco caliente cede una cantidad de calor | Qc | sin variar su temperatura TC, por lo que

y la variación de entropía del universo en este paso es
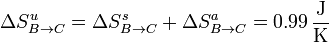
Aunque la entropía del ambiente disminuye, la del sistema aumenta más, resultando una variación neta positiva, como corresponde a un proceso posible e irreversible.
5.3 Enfriamiento a volumen constante
En el paso C→A, lo que se conserva es el volumen, así que usamos la expresión en términos de la temperatura y el volumen
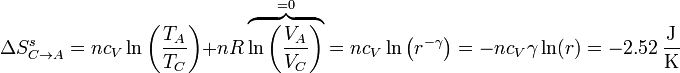
El resultado es exactamente el mismo que en el paso anterior, pero con signo contrario. Esto debía ser necesariamente así ya que con este proceso se cierra el ciclo y, al ser la entropía una función de estado, su variación neta debe ser nula (para el sistema, no para el universo).
De nuevo, podemos suponer un proceso reversible que lleve de C a A. En este caso un enfriamiento gradual a volumen constante
Una forma alternativa de calcular esta variación de entropía es imaginando un proceso reversible que conecte los estados inicial y final. Si suponemos una variación gradual de la temperatura a presión constante

La variación de entropía del ambiente en este proceso la hallamos ahora aplicando que el foco frío absorbe una cantidad de calor | Qf | a una temperatura constante TA
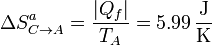
y la variación de entropía del universo es
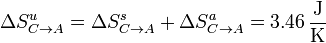
De nuevo obtenemos una variación neta positiva, ya que este paso también es posible e irreversible.
5.4 Producción neta de entropía
Considerando el ciclo completo, la variación de entropía del sistema es nula, por tratarse de una función de estado en un proceso cíclico:
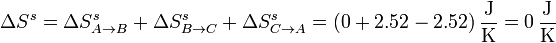
La entropía del ambiente, en cambio, aumenta,
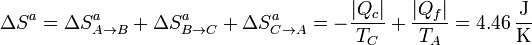
La variación de la entropía del universo coincidirá con esta cantidad
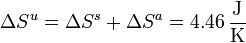
6 Trabajo perdido
El trabajo perdido es la diferencia entre el trabajo máximo posible (la exergía) y el realmente obtenido. El trabajo máximo lo da una máquina reversible que opere entre las dos temperaturas dadas.
El rendimiento de una máquina de este tipo es, en nuestro caso

Vemos que nuestra máquina térmica está muy lejos del máximo teórico. El cociente entre el rendimiento real y el máximo (lo que se llama el rendimiento de la segunda ley) es solo
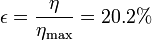
El trabajo máximo en un ciclo lo obtenemos a partir del calor absorbido y del rendimiento máximo
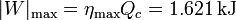
por lo que el trabajo perdido por ciclo es
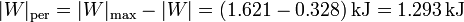
Este trabajo perdido puede también calcularse a partir de la producción de entropía, ya que ésta mide la irreversibilidad del proceso, que se manifiesta en un exceso de calor de desecho
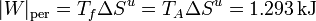
En comparación con el trabajo máximo, el trabajo perdido supone una proporción
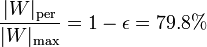
esto es, que se pierde el 80% del trabajo máximo posible.
La razón de que se trate de un ciclo tan ineficiente es que estamos considerando un ciclo Diesel en el que no hacemos uso de la potencia motriz del aire caliente. Este ciclo ficticio sería algo así como si el gasóleo se siquiera quemando todo el tiempo que el émbolo desciende y, cuando este llega abajo y volviera a subir, se procediera a vaciar la cámara. Es claro que estamos desaprovechando gran parte del trabajo que se podría sacar de la combustión del gas, ya que el quemarlo cuando el émbolo está abajo no produce beneficio alguno. Asimismo, esta combustión continuada implica un aumento grande de la temperatura del gas. Si hubiéramos tomado la relación de compresión igual a una típica en un motor diésel (p.ej, 18) resultaría una temperatura máxima del gas de 17000 K (¡el triple de la de la superficie del Sol!), lo cual es absurdo. Por ello debemos trabajar con una relación de compresión muy baja y presiones muy reducidas.







