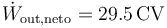Caso práctico de ciclo Otto

De Laplace

Contenido

1 Enunciado
2 Estados del ciclo
3 Trabajo y calor
4 Rendimiento
5 Potencia

1 Enunciado

Suponga un motor de gasolina de cuatro tiempos, de 1400 cm³ de cilindrada que se puede modelar mediante un ciclo Otto ideal con una relación de compresión de 8. Al inicio de la fase de compresión, el aire está a 100 kPa y 17°C. En la combustión se añaden 800 kJ/kg de calor. Determine la temperatura y la presión máximas que se producen en el ciclo, la salida de trabajo neto y el rendimiento de este motor.

Si este motor trabaja a 3000rpm, ¿cuánto es la potencia generada?

2 Estados del ciclo

El ciclo Otto ideal sirve para modelar el comportamiento de un motor de gasolina y está formado por dos isócoras y dos adiabáticas.

Estos cuatro procesos se pueden representar por segmentos rectos o curvos en un diagrama pV. Los vértices corresponden a 4 estados de equilibrio de forma que el proceso es A→B→C→D→A.

Denominaremos estado A al que tiene el gas antes de la compresión.

En este estado la temperatura es de 290 K y la presión es de 100 kPa.

El volumen inicial lo obtenemos de que conocemos la cilindrada

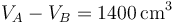
$V_A - V_B = 1400\,\mathrm{cm}^3$

y la relación de compresión

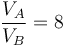
$\frac{V_A}{V_B} = 8$

Despejando y sustituyendo obtenemos que

$V_A=1600\,\mathrm{cm}^3\qquad\qquad V_B=200\,\mathrm{cm}^3$

Con esto ya tenemos el punto de partida

Estado	p (kPa)	T (K)	V (cm³)
A	100	290	1600

Para ir del estado A al B se realiza una compresión adiabática. Como suponemos que es cuasiestática, podemos aplicar la ley de Poisson

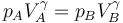
$p_AV_A^\gamma = p_B V_B^\gamma\,$

lo que nos permite hallar la presión en B

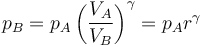
$p_B = p_A\left(\frac{V_A}{V_B}\right)^\gamma = p_A r^\gamma$

lo que da

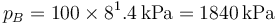
$p_B = 100\times 8^1.4\,\mathrm{kPa} = 1840\,\mathrm{kPa}$

Conocidas la presión y el volumen, tenemos la temperatura por la ley de los gases ideales

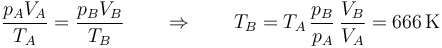
$\frac{p_AV_A}{T_A}=\frac{p_BV_B}{T_B}\qquad \Rightarrow\qquad T_B = T_A\,\frac{p_B}{p_A}\,\frac{V_B}{V_A}= 666\,\mathrm{K}$

lo que nos da el segundo vértice

Estado	p (kPa)	T (K)	V (cm³)
A	100	290	1600
B	1840	666	200

Para el tercer vértice, C, tenemos en primer lugar que el volumen no cambia

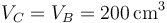
$V_C=V_B=200\,\mathrm{cm}^3$

para hallar la nueva temperatura debemos tener en cuenta el calor aportado por la combustión. El poder calorífico de la mezcla es de 800kJ/kg. La masa de mezcla que tenemos es aproximadamente la del aire, siendo su valor

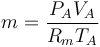
$m = \frac{P_AV_A}{R_mT_A}$

siendo $R m$ la constante del gas, que para el aire vale

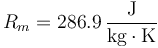
$R_m = 286.9\,\frac{\mathrm{J}}{\mathrm{kg}\cdot\mathrm{K}}$

Esto nos da una masa

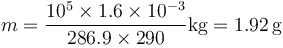
$m = \frac{10^5\times 1.6\times 10^{-3}}{286.9\times 290}\mathrm{kg}=1.92\,\mathrm{g}$

con lo cual el calor liberado en la combustión es aproximadamente

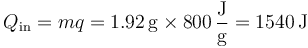
$Q_\mathrm{in}= mq=1.92\,\mathrm{g}\times 800\,\frac{\mathrm{J}}{\mathrm{g}} = 1540\,\mathrm{J}$

Puesto que no se realiza trabajo en este paso, este calor es igual al incremento de la energía interna

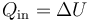
$Q_\mathrm{in}=\Delta U\,$

Cuando el cambio de temperatura es muy grande, la relación entre U y T es una función complicada, por lo que el procedimiento correcto es ir a una tabla y ver que temperatura corresponde a una determinada energía.

Si hacemos la aproximación de capacidades caloríficas constantes, podemos estimar la temperatura final a partir de

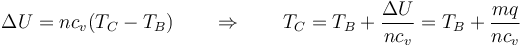
$\Delta U = n c_v(T_C-T_B) \qquad\Rightarrow\qquad T_C = T_B + \frac{\Delta U}{nc_v} = T_B + \frac{mq}{nc_v}$

puesto que m/n es el peso molecular (28.96 g/mol para el aire) y $c v = 5 R / 2$ para el aire queda

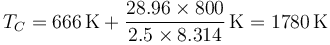
$T_C = 666\,\mathrm{K}+\frac{28.96\times 800}{ 2.5\times 8.314}\,\mathrm{K}=1780\,\mathrm{K}$

Mediante la ley de los gases ideales hallamos la presión

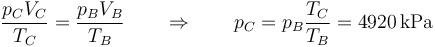
$\frac{p_C V_C}{T_C}=\frac{p_BV_B}{T_B}\qquad\Rightarrow\qquad p_C =p_B\frac{T_C}{T_B}=4920\,\mathrm{kPa}$

lo que nos da la siguiente fila de la tabla

Estado	p (kPa)	T (K)	V (cm³)
A	100	290	1600
B	1840	666	200
C	4920	1780	200

En el estado D el volumen vuelve a ser el inicial

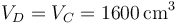
$V_D=V_C=1600\,\mathrm{cm}^3$

y por ser adiabática la expansión podemos emplear de nuevo la ley de Poisson

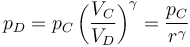
$p_D = p_C\left(\frac{V_C}{V_D}\right)^\gamma =\frac{p_C}{r^\gamma}$

lo que da

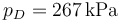
$p_D = 267\,\mathrm{kPa}$

y la temperatura de este estado

$\frac{p_AV_A}{T_A}=\frac{p_DV_D}{T_D}\qquad \Rightarrow\qquad T_D = T_A\,\frac{p_D}{p_A}=775\,\mathrm{K}$

completándose la tabla

Estado	p (kPa)	T (K)	V (cm³)
A	100	290	1600
B	1840	666	200
C	4920	1780	200
D	267	775	1600

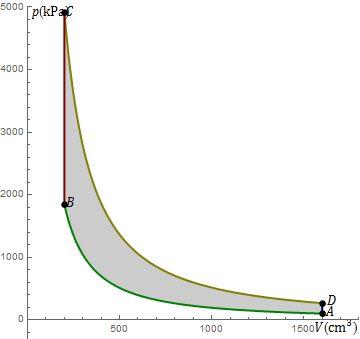
La temperatura y la presión máximas se alcanzan al final de la combustión, en el estado C, siendo p = 4.9MPa y T = 1780K.

3 Trabajo y calor

El calor que entra en el proceso de combustión ya lo hemos calculado

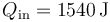
$Q_\mathrm{in} = 1540\,\mathrm{J}$

Este calor se puede calcular también a partir del incremento en la energía interna

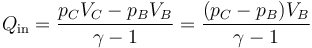
$Q_\mathrm{in}=\frac{p_CV_C-p_BV_B}{\gamma-1}=\frac{(p_C-p_B)V_B}{\gamma-1}$

En los procesos adiabáticos no se intercambia calor, por lo que la única salida se produce en el escape D→A, en el cual no se realiza trabajo. Aplicamos de nuevo el primer principio de la termodinámica

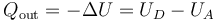
$Q_\mathrm{out}=-\Delta U = U_D-U_A\,$

Suponiendo de nuevo calores específicos constantes

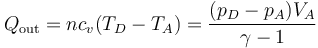
$Q_\mathrm{out}=nc_v(T_D-T_A)=\frac{(p_D-p_A)V_A}{\gamma-1}$

lo que da

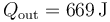
$Q_\mathrm{out} = 669\,\mathrm{J}$

El trabajo neto es igual a la diferencia entre el calor que entra y el que sale

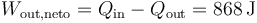
$W_\mathrm{out,neto}=Q_\mathrm{in}-Q_\mathrm{out}=868\,\mathrm{J}$

Este trabajo se puede hallar también calculando el trabajo que entra en la compresión y el que sale en la expansión, a partir del cambio en la energía interna en esos procesos adiabáticos

$W_\mathrm{in}=U_B-U_A=\frac{p_BV_B-p_AV_A}{\gamma-1}\qquad\qquad W_\mathrm{out}=U_C-U_D=\frac{p_CV_C-p_DV_D}{\gamma-1}$

4 Rendimiento

Conocidos el calor que entra y el trabajo neto que sale, obtenemos el rendimiento del ciclo

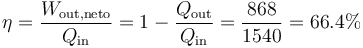
$\eta = \frac{W_\mathrm{out,neto}}{Q_\mathrm{in}}=1-\frac{Q_\mathrm{out}}{Q_\mathrm{in}}=\frac{868}{1540}= 66.4\%$

Este rendimiento también se puede calcular a partir de las temperaturas de los vértices

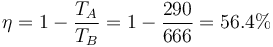
$\eta = 1 - \frac{T_A}{T_B}= 1- \frac{290}{666}=56.4\%$

y a partir de la fórmula para el ciclo Otto ideal

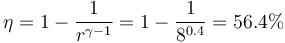
$\eta = 1-\frac{1}{r^{\gamma-1}} = 1 -\frac{1}{8^{0.4}} = 56.4\%$

5 Potencia

Tenemos el trabajo neto generado en un ciclo. Si el motor trabaja a 3000rpm (revoluciones por minuto)quiere decir que efectúa 50 ciclos por segundo.

Sin embargo, al ser un motor de cuatro tiempos, cada cilindro solo realiza trabajo la mitad de los ciclos, es decir 25 veces por segundo (la otra miitad la emplea en admitir gases en el cilindro y en expulsarlos de él).

Esto da la potencia

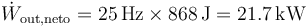
$\dot{W}_\mathrm{out,neto} = 25\,\mathrm{Hz}\times 868\,\mathrm{J}=21.7\,\mathrm{kW}$

En caballos, definidos omo 1CV = 735.49875W, la potencia se expresa

$\dot{W}_\mathrm{out,neto} = 29.5\,\mathrm{CV}$

Caso práctico de ciclo Otto

De Laplace

Contenido

1 Enunciado

2 Estados del ciclo

3 Trabajo y calor

4 Rendimiento

5 Potencia

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES