De Laplace

Contenido

1 Problemas del boletín
2 Otros problemas

1 Problemas del boletín

1.1 Sistema de vectores deslizantes equivalente a un sistema de vectores deslizantes

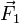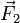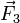Se tiene un s.v.d. formado por tres vectores $\vec{F}_1$ , $\vec{F}_2$ y $\vec{F}_3$ , con puntos de aplicación $P 1$ , $P 2$ y $P 3$ .

$\begin{array}{lcl} \vec{F}_1 = \vec{\jmath}\,\mathrm{(N)}&\qquad\qquad&P_1(1,0,0)\,\mathrm{(m)}\\ \vec{F}_2 = -\vec{\imath}\,\mathrm{(N)}&\qquad\qquad&P_2(0,1,0)\,\mathrm{(m)}\\ \vec{F}_3 = \vec{\imath} + \vec{\jmath}\,\mathrm{(N)}&\qquad\qquad&P_3(1,1,0)\,\mathrm{(m)} \end{array}$

Encuentra la resultante y el momento resultante en el origen.
¿Existe un s.v.d. formado por un vector suelto que sea dinámicamente equivalente al sistema original?

1.2 Varilla con peso y muelle horizontal

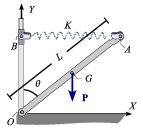
La varilla $O A$ , homogénea, de peso $P$ y longitud $L$ , está obligada a permanecer en el plano vertical fijo $O X Y$ . Su extremo $O$ se halla articulado al origen del sistema de referencia, mientras que su extremo $A$ está conectado, mediante un resorte elástico ideal de constante recuperadora $K$ y longitud natural nula, a un deslizador puntual $B$ que puede moverse sin rozamiento a lo largo del eje $O Y$ . El resorte $A B$ se mantiene perpendicular al eje $O Y$ en todo instante.

Representa el "diagrama de sólido libre" de la varilla teniendo en cuenta el teorema de las tres fuerzas.
Determina el ángulo $θ$ que forma la varilla con el eje vertical $O Y$ en la posición de equilibrio (descartando las soluciones $θ = 0$ y $θ = π$ radianes)

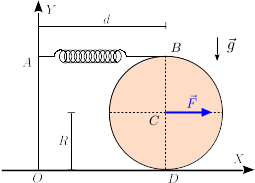
1.3 Disco sostenido por una armadura

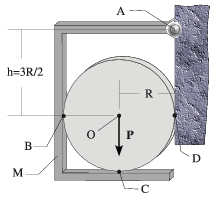
Un disco liso de radio $R$ y cuyo peso vale $P$ , está sostenido según se indica en la figura por la armadura $M$ de peso despreciable. El punto $A$ de dicha armadura se halla conectado a un muro vertical mediante un cojinete de sustentación y empuje sin rozamiento (par de revolución liso), siendo $h = 3 R / 2$ la distancia que separa sendas rectas horizontales que pasan por $A$ y por el centro del disco $O$ . Se pide:

Hallar las reacciones que el cojinete ejerce sobre la armadura en el punto A.
Hallar las reacciones ejercidas sobre el cilindro en los puntos de contacto B, C y D.

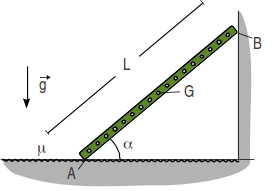
1.4 Varilla en dos puntos con contacto rugoso

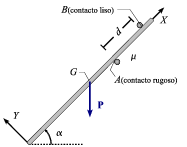
La barra homogénea de la figura tiene peso $P$ y se halla en equilibrio, si bien en situación de "deslizamiento inminentei", como consecuencia de haber quedado encajada entre los soportes puntuales $A$ (contacto rugoso de coeficiente de rozamiento estático $μ$ ) y $B$ (contacto liso). Conocidos el ángulo $α$ de inclinación de la barra con respecto a la horizontal, así como la distancia $d$ que separa a los dos soportes puntuales, se pide:

Desvincular razonadamente la barra ("diagrama de sólido libre")
Determinar la distancia $(x A - x G$ ) entre el centro de gravedad $G$ de la barra y el soporte puntual $A$ .
Calcular las reacciones vinculares ejercidas sobre la barra por los soportes puntuales $A$ y $B$ .

1.5 Varilla apoyada sobre un cuadrado con contacto rugoso

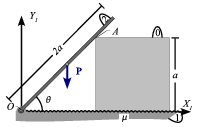
El esquema de la figura muestra una placa cuadrada de lado $a$ y espesor y peso despreciables (sólido "0"). Ésta se halla contenida en un plano vertical $O X 1 Y 1$ , con uno de sus lados en contacto con el eje horizontal $O X 1$ (sólido "1"). Dicho contacto es rugoso, con un coeficiente de rozamiento estático $μ$ . Al mismo tiempo, sobre el vértice $A$ de la placa se apoya una varilla pesada y homogénea, de peso $P$ y longitud $2 a$ (sólido "2"), con un contacto liso. La varilla se mantiene siempre en el plano vertical $O X 1 Y 1$ , y puede girar libremente alrededor de su extremo articulado sin rozamiento en el punto $O$ del eje horizontal fijo. Se pide:

Fragmentar el sistema de sólidos y representar sus correspondientes "diagramas de sólido libre".
El rango de valores del parámetro $θ$ para el que es posible el equilibrio estático del sistema, y las reacciones vinculares ejercidas sobre la varilla en dicha situación.

1.6 Deformación de un cable de ascensor

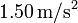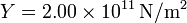Un ascensor puede llevar una carga máxima de 1000 kg (incluyendo su propia masa). Está suspendido de un cable de acero de 3.00 cm de diámetro y 300 m de longitud cuando está completamente desenrollado. La aceleración máxima del ascensor es $1.50\,\mathrm{m/s^2}$ . Si el aumento máximo de longitud del cable es de 3.00 cm ¿es seguro montarse en el ascensor? Dato: Módulo de Young del acero: $Y = 2.00\times10^{11}\,\mathrm{N/m^2}$ .

2 Otros problemas

2.1 Sistema de vectores deslizantes equivalente a un vector deslizante

Una fuerza 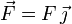$\vec{F} = F\,\vec{\jmath}$ actúa sobre un sólido rígido aplicada en el punto $P (a,0,0)$ . Encuentra un sistema de vectores deslizantes formado por tres fuerzas que sea equivalente a la fuerza $\vec{F}$ y esté aplicado en el origen de referencia.

2.2 Escalera apoyada en una pared

Una escalera de longitud $L$ se apoya en el suelo y una pared vertical de modo que el ángulo que forma con la horizontal es $α$ . El contacto con la pared es liso, mientras que con el suelo es rugoso con coeficiente de rozamiento estático $μ$ . La masa de la escalera es $m$ , y su peso está aplicado en su centro.

En condiciones de equilibrio estático, ¿cuanto vale el módulo de la fuerza de rozamiento en el apoyo en el suelo?
¿Qué condición debe cumplir el ángulo para que la escalera no deslice?

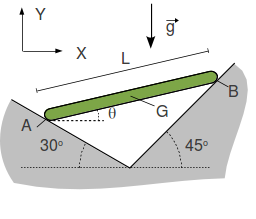
2.3 Varilla apoyada sobre dos rampas

Una barra de longitud $L$ y masa $m$ se apoya sobre dos planos inclinados como se indica en la figura. Los apoyos en los planos son lisos. El peso de la barra se aplica en su centro. Dibuja el diagrama de cuerpo libre de la barra.

Calcula las fuerzas de reacción vincular en los apoyos (puntos $A$ y $B$ ).
Calcula el valor del ángulo $θ$ para el que la barra se encuentra en equilibrio.
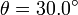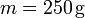Consideramos ahora una situación en la que el ángulo $θ$ vale $\theta = 30.0^{\circ}$ . En este caso el contacto en $A$ es rugoso mientras que en $B$ es liso. Calcula el valor del módulo de la fuerza de rozamiento en $A$ si la masa de la barra es $m=250\,\mathrm{g}$ .

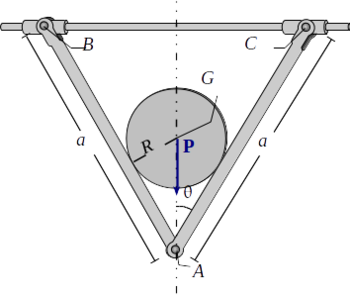
2.4 Disco apoyado en dos varillas en forma de V

En el esquema de la figura la barras $A B$ y $A C$ , ambas de longitud $a$ , están articuladas sin rozamiento en $A$ y con sus extremos $B$ y $C$ en un eje horizontal sobre el que pueden deslizar sin rozamiento. El peso de estas barras es despreciable en comparación con el peso $P$ de un disco homogéneo de radio $R$ que se apoya sin rozamiento sobre las barras, manteniéndose todo el sistema en un plano vertical (ver figura). Se pide:

Desvincular el sistema de sólidos y representar los correspondientes "diagramas de sólido libre".
Las reacciones vinculares en $B$ y $C$ para la posición de equilibrio.
La ecuación que determina la posición de equilibrio. ¿Que relación debe existir entre el radio del disco y la longitud de las barras para que el sistema esté en equilibrio en la posición correspondiente a $θ eq = π / 4$ ?

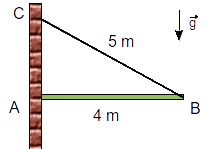
2.5 Barra apoyada en una parede sujeta por un cable

Una barra de longitud $L$ y masa $m$ está sujeta por un extremo a un cable que a su vez tienen su otro extremo anclado en la pared. El otro extremo de la barra se apoya en la pared, de modo que la barra se mantiene horizontal. El contacto en $A$ es rugoso. Determina las fuerzas que actúan sobre la barra en el punto en que se apoya en la pared. ¿Cuál es el valor mínimo del coeficiente de rozamiento para que el equilibrio sea posible? ¿Cuánto vale la tensión del cable en ese caso? El peso de la barra se aplica en su centro de masas.

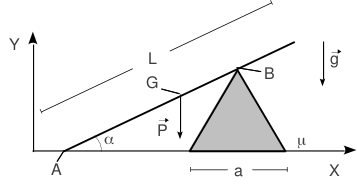
2.6 Barra apoyada sobre un triángulo

Una barra de longitud $L$ se apoya en el suelo y en el vértice de un triángulo equilátero de lado $a$ . El ángulo que forma la barra con el suelo es $α$ . El peso de la barra es $P$ , y se aplica en su punto medio $G$ . El peso del triángulo es despreciable. El contacto con el suelo es rugoso para la barra y el triángulo, con un coeficiente de rozamiento $μ$ . El contacto entre la barra y el triángulo en el punto $B$ es liso.

Dibuja el diagrama de cuerpo libre de la barra y el triángulo.
Calcula todas las fuerzas del apartado anterior en condiciones de equilibrio estático.
¿Que condición debe cumplir $α$ para que el triángulo no vuelque en ningun caso?
Analiza las condiciones que debe cumplir $μ$ para que se mantenga el equilibrio frente a deslizamiento.

2.7 Triángulo con muelle y rozamiento

Se tiene un triángulo equilátero homogéneo de peso $\vec{P}$ y lado $a$ . El peso está aplicado en el baricentro del triángulo, $G$ . El triángulo apoya uno de sus lados en una superficie rugosa, con coeficiente de rozamiento $μ$ . El vértice $A$ está unido a la pared con un muelle de constante elástica $k$ y longitud natural nula. El muelle se mantiene siempre horizontal, como se indica en la figura

Dibuja el diagrama de sólido libre del triángulo.
Encuentra las fuerzas que actúan sobre el triángulo en situación de equilibrio mecánico.
¿Que condición debe cumplir $μ$ para que el equilibrio se rompa por deslizamiento y no por vuelco?

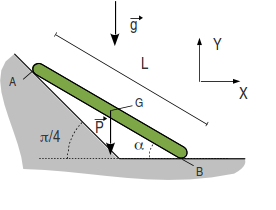
2.8 Barra apoyada sobre una pared inclinada

La barra de la figura forma un ángulo $α$ con la horizontal y está apoyada sobre una pared inclinada $π / 4$ . El peso de la barra está aplicado en su centro. El contacto en el punto $A$ es liso, mientras que en el punto $B$ es rugoso con un coeficiente de rozamiento estático $μ$ .

Dibuja el diagrama de sólido libre de la barra.
Considerando el ángulo $α$ como un dato, calcula las fuerzas sobre la barra en los puntos $A$ y $B$ .
¿Para que valores del ángulo $α$ es posible el equilibrio?

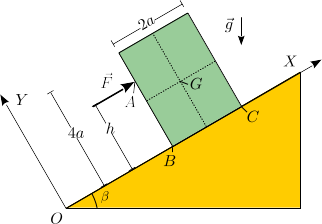
2.9 Vuelco en plano inclinado

Un bloque rectangular, de masa $m$ y lados $2 a$ y $4 a$ , descansa sobre un plano inclinado un ángulo $β$ respecto de la horizontal. Se aplica sobre el punto $A$ del bloque una fuerza 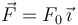$\vec{F}=F_0\,\vec{\imath}$ , con $F 0 > 0$ . La fuerza es horizontal al plano inclinado y el punto $A$ está a una distancia $h$ del plano. Consideramos en primera instancia que el contacto entre el bloque y el plano es liso. El ángulo $β$ cumple

$\mathrm{sen}\, \beta = \dfrac{3}{5}, \qquad \cos\beta = \dfrac{4}{5}.$

Dibuja el diagrama de cuerpo libre del bloque.
Encuentra el valor de $F 0$ para que haya equilibrio. Encuentra las expresiones de las fuerzas en esta situación.
Con las fuerzas obtenidas en el apartado anterior, encuentra las condiciones que debe cumplir $h$ para que el bloque no vuelque hacia la izquierda ni la derecha.
Considera ahora que hay rozamiento entre el bloque y el plano inclinado, con coeficiente de rozamiento estático $μ$ . Supongamos que $F 0 = m g$ . Determina las condiciones que deben cumplir $μ$ y $h$ para que haya equilibrio frente a deslizamiento y vuelco.

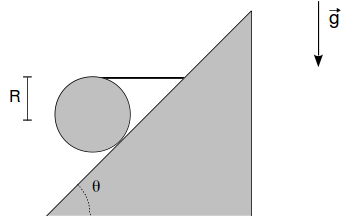
2.10 Esfera sobre un plano inclinado con una cuerda horizontal

Una esfera uniforme de masa $M$ y radio $R$ se mantiene en reposo sobre un plano inclinado un ángulo $θ$ mediante una cuerda horizontal, como se indica en la figura. El contacto entre la esfera y el plano es rugoso con coeficiente de rozamiento estático $μ$ .

Dibuja el diagrama de cuerpo libre de la esfera.
Calcula la tensión de la cuerda, la fuerza de rozamiento y la reacción del plano sobre la esfera.
Analiza los valores del ángulo para los cuales es posible el equilibrio.

2.11 Disco apoyado en un escalón

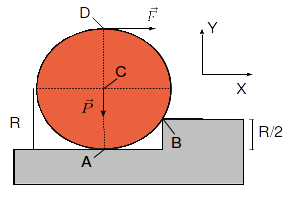
El disco de radio $R$ y peso $P$ de la figura sufre una fuerza horizontal de módulo $F$ aplicada en su punto más alto. El contacto en el punto $A$ es liso, mientras que el contacto en el punto $B$ es rugoso con coeficiente de rozamiento estático $μ$ .

Calcula las fuerzas sobre el disco en situación de equilibrio estático.
¿Qué condición debe cumplir el coeficiente de rozamiento para que pueda haber equilibrio estático?
En este último caso, ¿qué condición debe valer la fuerza $F$ para que el disco suba el escalón?

2.12 Barra articulada con momento aplicado

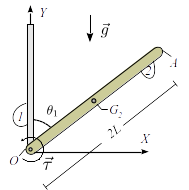
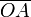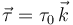En el sistema de la figura, la barra $\overline{OA}$ (sólido "2") tiene masa $m$ y longitud $2 L$ . La barra está articulada en el punto fijo $O$ de una barra vertical fija(sólido "1"). Se aplica un par $\vec{\tau}=\tau_0\,\vec{k}$ sobre la barra "2". El sistema está sometido a la gravedad.

¿Como debe ser el par aplicado para que el ángulo sea $θ 1 = π / 6$ ?
Ahora, manteniendo aplicado el par de la pregunta anterior, se apoya una barra homogénea "0", de masa $m$ y longitud $2 L$ , como se indica en la figura. La barra "0" se mantiene siempre horizontal. Todos los contactos son lisos.
¿Cuanto vale el ángulo de equilibrio en la nueva situación?
Calcula el par vincular sobre la barra "0" originado por el vínculo en $B$ es

2.13 Barra articulada en pared con muelle

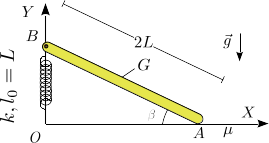
Una barra homogénea de masa $m$ y longitud $2 L$ está apoyada en el suelo en un extremo (punto $A$ ). El otro extremo ( $B$ ) está articulado en un eje vertical de modo que la barra puede rotar alrededor de $B$ y el punto $B$ puede deslizar sobre el eje. Un muelle de constante elástica $k$ y longitud natural $L$ conecta el punto $B$ con el origen de coordenadas $O$ . El muelle se mantiene vertical en todo momento. El contacto de la barra en $B$ es liso, mientras que es rugoso en $A$ con coeficiente estático de rozamiento $μ$ .

Dibuja el diagrama de cuerpo libre de la barra, indicando para que fuerzas el sentido es conocido a priori y para cuales no. Razona la respuesta.
Escribe las expresiones de las fuerzas que actúan sobre la barra.
Suponiendo que $β = π / 6$ , calcula el valor de las fuerzas que actúan sobre la barra en situación de equilibrio estático.
Calcula la reducción vincular en el punto $G$ usando las fuerzas obtenidas en el apartado anterior.
¿Qué condición debe cumplir $μ$ para que la situación de equilibrio sea posible?

2.14 Placa cuadrada pivotando conectada a un muelle

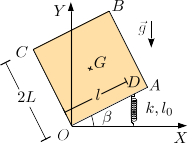
Una placa cuadrada homogénea de masa $m$ y lado $2 L$ se apoya sobre uno de sus extremos, el punto $O$ de la figura. Este vértice de la placa no se mueve nunca. Un muelle de constante elástica $k$ y longitud natural $l 0 = L$ está conectado a un punto $D$ del lado $O A$ de la placa. El otro extremo del muelle está en el eje $O X$ , de modo que el muelle es siempre vertical. La gravedad actúa como se indica en la figura. La masa de la placa es tal que $m g = k L$ .

Dibuja el diagrama de cuerpo libre del sólido rígido.
Encuentra las expresiones de las fuerzas que actúan sobre la placa.
Si tenemos $β = π / 3$ , encuentra el valor de $l$ para el que la placa está en equlibrio.
Suponiendo que $β = π / 4$ , calcula el par de fuerzas que habría que aplicar sobre la placa para que esté en equilibrio cuando el punto $D$ coincide con el $A$ (el muelle siempre está vert

2.15 Disco con muelle

El disco de la figura tiene masa $m$ y radio $R$ . El muelle tiene constante elástica $k$ y longitud natural nula. El muelle se mantiene siempre horizontal. Se aplica en el centro del disco $C$ una fuerza $\vec{F}$ horizontal. El contacto entre el disco y el suelo es rugoso con coeficiente de rozamiento estático $μ$ .

Dibuja el diagrama de cuerpo libre del disco.
¿Cuál debe ser el valor de $\vec{F}$ para que el disco esté en equilibrio estático?
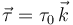Ahora, en vez de aplicar la fuerza $\vec{F}$ , se aplica sobre el disco un par de fuerzas $\vec{\tau}=\tau_0\,\vec{k}$ . ¿Cuanto debe valer $τ 0$ para que el disco esté en equilibrio estático?
Discute como se comporta la fuerza de rozamiento cuando se aplica la fuerza y cuando se aplica el par de fuerzas.

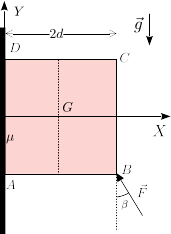
2.16 Placa cuadrada empujada contra una pared

Una placa cuadrada de masa $m$ y lado $2 d$ se apoya en una pared vertical rugosa con coeficiente de rozamiento estático $μ = 1$ . Una fuerza $\vec{F}$ empuja el bloque contra la pared. El módulo de la fuerza es $F 0$ y forma un ángulo $β$ con el eje $Y 1$ . La gravedad actúa como se indica en la figura. El ángulo $β$ verifica

$\mathrm{sen}\,\beta = \dfrac{3}{5}, \qquad \cos\beta = \dfrac{4}{5}.$

Dibuja el diagrama de cuerpo libre de la placa.
Calcula el valor de las fuerzas que actúan sobre la placa en condiciones de equilibrio estático.
¿Que condiciones debe cumplir $F$ para que la placa no deslice?
¿Que condiciones debe cumplir $F$ para que la placa no vuelque respecto a la pared?
¿Que condiciones debe cumplir $F$ para que la placa ni deslice ni vuelque respecto a la pared?

Problemas de Estática del sólido rígido (G.I.C.)