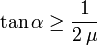Escalera apoyada en una pared, Enero 2012 (G.I.C.)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

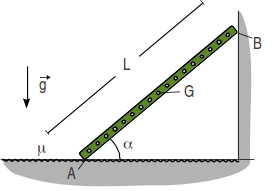
Una escalera de longitud $L$ se apoya en el suelo y una pared vertical de modo que el ángulo que forma con la horizontal es $α$ . El contacto con la pared es liso, mientras que con el suelo es rugoso con coeficiente de rozamiento estático $μ$ . La masa de la escalera es $m$ , y su peso está aplicado en su centro.

En condiciones de equilibrio estático, ¿cuanto vale el módulo de la fuerza de rozamiento en el apoyo en el suelo?
¿Qué condición debe cumplir el ángulo para que la escalera no deslice?

2 Solución

2.1 Diagrama de sólido libre

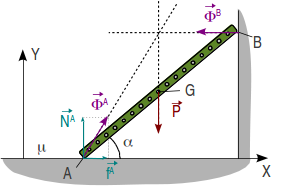
El apoyo en la pared es liso, por lo que la fuerza de reacción vincular en la pared es perpendicular a ella. En el suelo el apoyo es liso, y por tanto la fuerza de reacción tiene una componente normal y otra tangencial al suelo. El peso está aplicado en el centro de la escalera. La figura muestra las fuerzas que actúan sobre el sólido rígido y el punto en el que se aplican. Al dibujar las fuerzas se ha tenido en cuenta el teorema de los tres centros, de modo que las rectas soportes de las tres fuerzas deben cortarse en un punto.

Usando los ejes de la figura, las fuerzas sobre la escalera pueden expresarse como

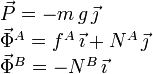
$\begin{array}{l} \vec{P} = -m\,g\,\vec{\jmath}\\ \vec{\Phi}^A = f^A\,\vec{\imath} + N^A\,\vec{\jmath}\\ \vec{\Phi}^B = -N^B\,\vec{\imath} \end{array}$

2.2 Valor de la fuerza de rozamiento en el apoyo sobre el suelo

Para que la escalera esté en equilibrio debe cumplirse que la fuerza neta sobre ellas sea cero y que el momento neto respecto de cualquier punto sea cero.

Aplicamos la condición de fuerza neta cero

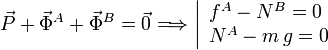
$\vec{P} + \vec{\Phi}^A + \vec{\Phi}^B =\vec{0} \Longrightarrow \left| \begin{array}{l} f^A - N^B = 0\\ N^A - m\,g = 0 \end{array} \right.$

Tenemos tres incógnitas: $N A$ , $f A$ y $N B$ . La tercera ecuación se obtiene de imponer que el momento neto es nulo respecto a cualquier punto. Escogemos el punto $A$ para calcular los momentos. Tenemos

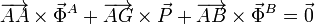
$\overrightarrow{AA}\times\vec{\Phi}^A + \overrightarrow{AG}\times\vec{P} + \overrightarrow{AB}\times\vec{\Phi}^B=\vec{0}$

Los vectores de posición son

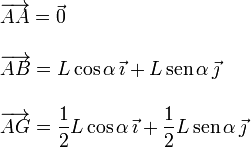
$\begin{array}{l} \overrightarrow{AA} = \vec{0}\\ \\ \overrightarrow{AB} = L\cos\alpha\,\vec{\imath} + L\,\mathrm{sen}\,\alpha\,\vec{\jmath} \\ \\ \overrightarrow{AG} = \dfrac{1}{2}L\cos\alpha\,\vec{\imath} + \dfrac{1}{2}L\,\mathrm{sen}\,\alpha\,\vec{\jmath} \end{array}$

Los momentos de cada una de las fuerzas son

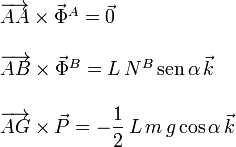
$\begin{array}{l} \overrightarrow{AA}\times\vec{\Phi}^A = \vec{0} \\ \\ \overrightarrow{AB}\times\vec{\Phi}^B = L\,N^B\,\mathrm{sen}\,\alpha\,\vec{k}\\ \\ \overrightarrow{AG}\times\vec{P} = -\dfrac{1}{2}\,L\,m\,g\cos\alpha\,\vec{k} \end{array}$

La suma de los tres momentos debe ser cero

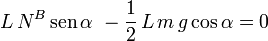
$L\,N^B\,\mathrm{sen}\,\alpha\ -\dfrac{1}{2}\,L\,m\,g\cos\alpha = 0$

Con esto tenemos tres ecuaciones para tres incógnitas. Resolviendo tenemos

$\begin{array}{l} N^B = \dfrac{m\,g}{2\tan\alpha}\\ \\ N^A = m\,g \\ \\ f^A = \dfrac{m\,g}{2\tan\alpha} \end{array}$

La fuerza de rozamiento es $f A$ . Observemos que no es igual al coeficiente de rozamiento por el módulo de la normal. Eso sólo ocurre en situación de deslizamiento inminente.

2.3 Condición sobre el ángulo

Cuanto menor sea el ángulo $α$ , mayor debe ser el valor de la fuerza de rozamiento $f A$ . Pero esta fuerza tiene un valor máximo

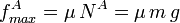
$f^A_{max} = \mu\,N^A = \mu\,m\,g$

Para que el apoyo en el suelo no deslice, la fuerza de rozamiento debe ser menor que ese valor máximo. La condición de equilibrio es

$\dfrac{m\,g}{2\tan\alpha} \leq \mu\,m\,g$

La condición sobre el ángulo puede escribirse

$\tan\alpha\geq \dfrac{1}{2\,\mu}$

Escalera apoyada en una pared, Enero 2012 (G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Diagrama de sólido libre

2.2 Valor de la fuerza de rozamiento en el apoyo sobre el suelo

2.3 Condición sobre el ángulo

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES