Entrar Página Discusión Historial Go to the site toolbox

Triángulo con muelle y rozamiento

De Laplace

Contenido

1 Enunciado

(Primer Parcial, Enero 2010, P2)

Se tiene un triángulo equilátero homogéneo de peso \vec{P} y lado a. El peso está aplicado en el baricentro del triángulo, G. El triángulo apoya uno de sus lados en una superficie rugosa, con coeficiente de rozamiento μ. El vértice A está unido a la pared con un muelle de constante elástica k y longitud natural nula. El muelle se mantiene siempre horizontal, como se indica en la figura

  1. Dibuja el diagrama de sólido libre del triángulo.
  2. Encuentra las fuerzas que actúan sobre el triángulo en situación de equilibrio mecánico.
  3. ¿Que condición debe cumplir μ para que el equilibrio se rompa por deslizamiento y no por vuelco?

2 Solución

2.1 Diagrama de sólido libre

El diagrama de sólido libre se construye dibujando el sólido y las fuerzas que actúan sobre él, tanto las activas como las de reacción vincular y rozamiento. En este problema las fuerzas activas son el peso y la fuerza elástica del muelle. El primero actúa en la dirección vertical apuntado hacia abajo (vector \vec{P} verde en la figura). Como el triángulo es homogéneo se aplica en su baricentro, como dice el enunciado. El muelle tiene longitud natural nula, por lo que tiende siempre a disminuir su longitud. 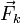La fuerza correspondiente sobre el triángulo se aplica en el vértice A, con dirección horizontal y sentido hacia la izquierda (vector \vec{F}_k azul en la figura)

El suelo ejerce una fuerza distribuida sobre toda la superficie del triángulo. Al ser un vínculo rugoso estas fuerzas tienen componente normal y tangente al suelo. El conjunto de las normales forman un sistema de vectores deslizantes paralelos. Su resultante es la f.r.v. del suelo sobre el triángulo, \vec{N}. El conjunto de las fuerzas horizontales son vectores cuya recta soporte es el eje X. Su resultante es la fuerza de rozamiento del suelo sobre el sólido, \vec{F}_R. La suma de la f.r.v. y la fuerza de rozamiento es \vec{\Phi} . Esta fuerza se representa en el diagrama en punto de la base del triángulo (punto C). La localización del punto C depende de las fuerzas activas.

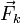Al pintar el vector \vec{\Phi} tenemos en cuenta el teorema de las tres fuerzas, que dice que si un sólido está sometido a tres fuerzas coplanarias, para que haya equilibrio mecánico las tres fuerzas deben ser concurrentes. En esta caso las tres fuerzas son \vec{P} , \vec{F}_k y \vec{\Phi} . Los puntos de aplicación y direcciones del peso y la fuerza del muelle están determinados por la geometría. Por tanto es la f.r.v. \vec{\Phi} la que debe ajustarse, y su recta soporte tiene que ser la que pasa por los puntos C y A.

Nota: De aquí podemos saber que el punto C necesariamente debe estar a la izquierda del baricentro del triángulo. Veamos por qué. Las únicas fuerzas que actúan en la dirección horizontal son la del muelle y la componente de rozamiento de \vec{\Phi} . Sabemos que la fuerza del muelle tira del triángulo hacia la izquierda. Entonces la componente de rozamiento tiene que apuntar hacia la derecha. Pero entonces, si el punto C estuviera a la derecha de G, la f.r.v. 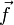\vec{\Phi} no podría pasar por el punto A, pues \vec{f} apuntaría hacia la derecha y \vec{N} hacia arriba.

2.2 Expresión de las fuerzas

Utilizando el sistema de referencia OXY de la figura, la expresión vectorial de las fuerzas son

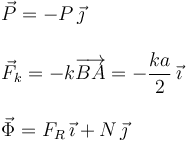
\begin{array}{l} \vec{P} = - P\,\vec{\jmath} \\ \\ \displaystyle\vec{F}_k = -k\overrightarrow{BA}=-\frac{ka}{2}\,\vec{\imath}\\ \\ \vec{\Phi} = F_R\,\vec{\imath} + N\,\vec{\jmath} \end{array}

Hemos escrito el peso de modo que el número P sea positivo, para que \vec{P} apunte hacia abajo. La fuerza del muelle viene dada por la ley de Hooke, teniendo en cuenta que su longitud natural es nula y que la distancia entre los puntos B y A es la mitad del lado del triángulo. Los signos de FR y N no los sabemos a priori, aunque basándonos en el diagrama de sólido libre esperamos que ambos sean positivos.

Para determinarlos aplicamos la condición de que el sistema de fuerzas que actúa sobre el sólido debe tener resultante nula, esto es

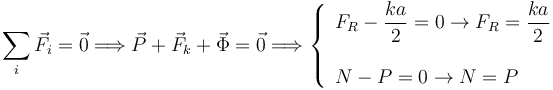
\sum\limits_{i}\vec{F}_i=\vec{0} \Longrightarrow \vec{P} + \vec{F}_k + \vec{\Phi}=\vec{0} \Longrightarrow \left\{ \begin{array}{l} \displaystyle F_R-\frac{ka}{2}=0 \to F_R=\frac{ka}{2}\\ \\ N - P = 0 \to N=P \end{array} \right.

Así pues, las fuerzas que actúan sobre el sólido cuando está en equilibrio son

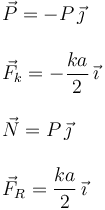
\begin{array}{l} \vec{P} = - P\,\vec{\jmath} \\ \\ \displaystyle\vec{F}_k = -\frac{ka}{2}\,\vec{\imath}\\ \\ \displaystyle \vec{N} = P\,\vec{\jmath} \\ \\ \displaystyle \vec{F}_R = \frac{ka}{2}\,\vec{\imath} \end{array}

Nota: Observemos que no hemos impuesto la condición de deslizamiento inminente. El coeficiente de rozamiento todavía no ha aparecido.

2.3 Condición para μ

Nos preguntan que condición debe cumplir el coeficiente de rozamiento μ para que el equilibrio se rompa por deslizamiento y no por vuelco. Analicemos cada una de estas condiciones.

2.3.1 Deslizamiento

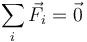El sólido desliza si se incumple la condición de equilibrio \sum\limits_i\vec{F}_i=\vec{0} . La normal siempre se adapta para compensar el peso, pero la fuerza de rozamiento tiene un valor máximo. El triángulo desliza si este valor máximo es incapaz de contener a la fuerza del muelle. Por tanto, para que haya deslizamiento tiene que cumplirse

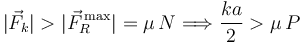
\displaystyle |\vec{F}_k| > |\vec{F}_{R}^{\,\mathrm{max}}| = \mu\,N \Longrightarrow \frac{ka}{2} > \mu\,P

Podemos escribir esta desigualdad como una condición de máximo para el peso

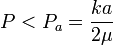
\displaystyle P < P_a = \frac{ka}{2\mu}

2.3.2 Vuelco

El equilibrio frente a vuelco puede estudiarse de varias formas. Vamos a hacerlo calculando la posición del punto C en la base del triángulo. Luego lo haremos de otra manera.

Para que el triángulo no vuelque debe cumplirse la otra condición de equilibrio estático del sólido rígido: el momento resultante del sistema de fuerzas debe ser nulo en cualquier punto. Vamos a calcular el momento respecto al punto O. Tenemos

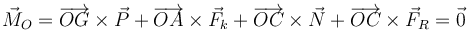
\vec{M}_O = \overrightarrow{OG}\times\vec{P} + \overrightarrow{OA}\times\vec{F}_k + \overrightarrow{OC}\times\vec{N} + \overrightarrow{OC}\times\vec{F}_R= \vec{0}

Vamos a calcular cada uno de los productos vectoriales

2.3.2.1 Peso

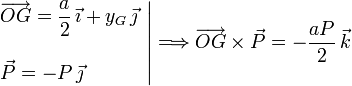
\left. \begin{array}{l} \displaystyle \overrightarrow{OG} = \frac{a}{2}\,\vec{\imath} + y_G\,\vec{\jmath}\\ \\ \vec{P}= -P\,\vec{\jmath} \end{array} \right| \Longrightarrow \overrightarrow{OG}\times\vec{P} = -\frac{aP}{2}\,\vec{k}

No hace falta calcular yG, pues no aparece en el producto vectorial (es un tercio de la altura del triángulo).

2.3.2.2 Fuerza del muelle

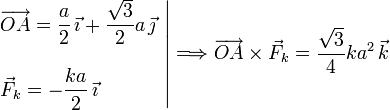
\left. \begin{array}{l} \displaystyle \overrightarrow{OA} = \frac{a}{2}\,\vec{\imath} + \frac{\sqrt{3}}{2}a\,\vec{\jmath}\\ \\ \displaystyle\vec{F}_k= -\frac{ka}{2}\,\vec{\imath} \end{array} \right| \Longrightarrow \overrightarrow{OA}\times\vec{F}_k = \frac{\sqrt{3}}{4}ka^2\,\vec{k}

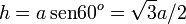La componente en Y del vector \overrightarrow{OA} es la altura del triángulo. Esta vale h=a\,\mathrm{sen}60^o=\sqrt{3}a/2 . También puede obtenerse usando el teorema de Pitágoras.

2.3.2.3 Fuerza de reacción vincular

El momento respecto a O de la fuerza de rozamiento es cero, pues \overrightarrow{OC} y \vec{F}_R son paralelos.

Vamos a calcular el momento de la f.r.v. No sabemos a priori donde está el punto C. Lo colocamos a una distancia d del punto O. La condición de equilibrio nos dará el valor de d

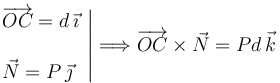
\left. \begin{array}{l} \displaystyle \overrightarrow{OC} = d\,\vec{\imath} \\ \\ \displaystyle\vec{N}= P\,\vec{\jmath} \end{array} \right| \Longrightarrow \overrightarrow{OC}\times\vec{N} = Pd\,\vec{k}

La suma de todos los momentos debe anularse. Esto nos da una ecuación para la distancia d

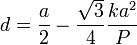
\displaystyle d = \frac{a}{2} - \frac{\sqrt{3}}{4}\frac{ka^2}{P}

Esto quiere decir que para que el momento resultante sea nulo, el punto C de aplicación de \vec{\Phi} debe venir dado por este valor de d. pero esto sólo es físicamente posible si el punto C está dentro de la base del triángulo. Entonces, para que el triángulo no vuelque debe cumplirse la igualdad

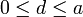
0\leq d\leq a

Si d < 0 el triángulo vuelca hacia la izquierda. Si d > a vuelca hacia la derecha. Veamos cada uno de estos dos casos

2.3.2.4 Vuelco por la derecha

Para que vuelque hacia la derecha el punto C debe salirse por la izquierda, esto es,

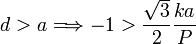
d>a \Longrightarrow -1 > \frac{\sqrt{3}}{2}\frac{ka}{P}

Pero esta situación no puede darse nunca, pues el número de la derecha es siempre positivo y nunca puede ser menor que un número negativo. Es decir, el triángulo nunca podrá volcar hacia la derecha. Esto tiene sentido, pues el muelle tira del triángulo hacia la izquierda, nunca podrá hacer que vuelque hacia la derecha.

Nota: Esto está relacionado con el hecho de que el teorema de las tres fuerzas impone que el punto C esté a la izquierda de G. La ecuación que da el valor de d nos dice que su valor es siempre menor que a / 2.

2.3.2.5 Vuelco por la izquierda

Para que ocurra este debe cumplirse

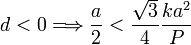
d<0 \Longrightarrow \frac{a}{2}<\frac{\sqrt{3}}{4}\frac{ka^2}{P}

Esto si que puede ocurrir. La condición para que el triángulo no vuelque es

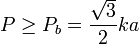
P \geq P_b = \frac{\sqrt{3}}{2}ka

2.3.3 Condición de sí deslizamiento y no vuelco

Resumiendo, para que ocurra lo que nos pide el enunciado, que pueda haber deslizamiento, pero no vuelco, deben cumplirse a la vez estas dos condiciones

P<P_a=\frac{ka}{2\mu}\qquad \qquad \qquad P\geq P_b = \frac{\sqrt{3}}{2}ka

Dicho de otro modo

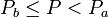
P_b \leq P < P_a

Pero para que esto sea posible debe ocurrir

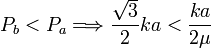
P_b < P_a \Longrightarrow \frac{\sqrt{3}}{2}ka<\frac{ka}{2\mu}

Es decir, la condición que debe cumplir el coeficiente de rozamiento es

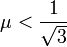
\mu < \frac{1}{\sqrt{3}}

Tiene sentido que la condición establezca un valor máximo para el coeficiente de rozamiento. Si éste es grande, el deslizamiento no es posible, pero el vuelco sí. Debe ser lo bastante pequeño como para que la condición de equilibrio frente a deslizamiento se incumpla antes que la de equilibrio frente a vuelco.

2.4 Análisis alternativo del vuelco

En este apartado vamos a analizar el equilibrio frente a vuelco de otra forma. Por supuesto, obtendremos los mismos resultados que con la técnica anterior.

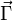Ahora consideramos que la desvinculación del contacto entre el suelo y el triángulo aparecen una f.r.v. \vec{\Phi} y un par de reacción vincular \vec{\Gamma} . El vector \vec{\Phi} no depende del punto de reducción , pues la resultante de un sistema de vectores deslizantes es un vector libre, pero el par de desvinculación sí. Supongamos que reducimos en el extremo derecho del triángulo (punto D). La reducción del conjunto de fuerzas en el vínculo entre el suelo y el triángulo en el punto D es

S^D = [\,\vec{\Phi}=f\,\vec{\imath}+N\,\vec{\jmath}\quad;\quad \vec{\Gamma}^D = -\Gamma^D\,\vec{k}\,]

Para que no vuelque hacia la derecha, el par de la distribución de f.r.v. en D tiene que ir en el sentido negativo del eje Z, como indica la figura. Así pues, el número ΓD en la reducción tiene que ser positivo.

El momento de las fuerzas activas respecto a D es

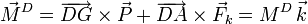
\vec{M}^D = \overrightarrow{DG}\times\vec{P} + \overrightarrow{DA}\times\vec{F}_k = M^D\,\vec{k}

La condición de equilibrio es que el momento resultante total sea nulo

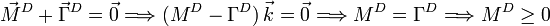
\vec{M}^D + \vec{\Gamma}^D=\vec{0} \Longrightarrow (M^D - \Gamma^D)\,\vec{k}=\vec{0} \Longrightarrow M^D = \Gamma^D \Longrightarrow M^D \geq 0

Dicho de otro modo, para que no vuelque hacia la derecha el par resultante de las fuerzas activas debe apuntar en la dirección positiva del eje Z. Haciendo el cálculo se obtiene

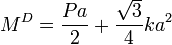
M^D = \frac{Pa}{2} + \frac{\sqrt{3}}{4}ka^2

Este número es siempre positivo, por lo que la condición de equilibrio frente a vuelco por la derecha se cumple siempre.


Ahora reducimos en el extremo izquierdo. Se tiene

S^O = [\,\vec{\Phi}=f\,\vec{\imath}+N\,\vec{\jmath}\quad;\quad \vec{\Gamma}^O = \Gamma^O\,\vec{k}\,]

El par de la distribución de f.r.v. en O tiene que ir en el sentido positivo del eje Z, como indica la figura. Así pues, el número ΓO en la reducción tiene que ser positivo.

El momento de las fuerzas activas respecto a O es

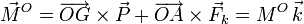
\vec{M}^O = \overrightarrow{OG}\times\vec{P} + \overrightarrow{OA}\times\vec{F}_k = M^O\,\vec{k}

La condición de equilibrio es que el momento resultante total sea nulo

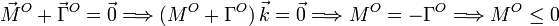
\vec{M}^O + \vec{\Gamma}^O=\vec{0} \Longrightarrow (M^O + \Gamma^O)\,\vec{k}=\vec{0} \Longrightarrow M^O = -\Gamma^O \Longrightarrow M^O \leq 0

Dicho de otro modo, para que no vuelque hacia la izquierda el par resultante de las fuerzas activas debe apuntar en la dirección negativa del eje Z. Haciendo el cálculo se obtiene

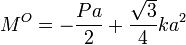
M^O = -\frac{Pa}{2} + \frac{\sqrt{3}}{4}ka^2

Imponiendo que MO sea negativo o nulo reobtenemos la condición de no vuelco hacia la izquierda.

2.5 Errores típicos encontrados en la corrección

  1. La fuerza de rozamiento no es siempre igual a μN. Esto sólo es así en la situación de deslizamiento inminente. La expresión de las fuerzas del segundo apartado se encuentra sin tener que imponer deslizamiento inminente.
  2. La condición para que haya deslizamiento inminente no es que la fuerza de rozamiento sea máxima, sino que la fuerza del muelle sea mayor que la fuerza de rozamiento máxima.
  3. Mucha gente ha simplemente ignorado el análisis de equilibrio frente a vuelco.
  4. La normal no tiene por qué estar aplicada debajo del peso. Algunos dicen que para que se anulen \vec{N} y \vec{P} tienen que ser colineales. Eso no es verdad. Cuando se calcula la resultante de un sistema de vectores deslizantes estos se consideran libres.
  5. En algunos exámenes se añade una f.r.v. en el punto A, con lo cual sobre ese punto quedan aplicada dos fuerzas, la del muelle y esta f.r.v. Las f.r.v. sólo aparecen en los vínculos, no en las fuerzas activas.
  6. En Física los vectores tienen flechas. No es que seamos maniáticos, es que si no se ponen la gente hace mal los cálculos y mezclan vectores con escalares.
  7. Un alumno/a de Ingeniería debería saber cuanto vale el seno y el coseno de 30o y 60o. Pero si por alguna razón no se acuerda uno del valor, hay que saber buscar caminos alternativos para calcular la altura del triángulo. Por ejemplo, usando el teorema de Pitágoras.
Obtenido de "http://tesla.us.es/wiki/index.php/Tri%C3%A1ngulo_con_muelle_y_rozamiento"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 12:55, 10 sep 2012. - Esta página ha sido visitada 5.018 veces. - Aviso legal - Acerca de Laplace