Barra apoyada sobre una pared inclinada, Diciembre 2012 (G.I.C.)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

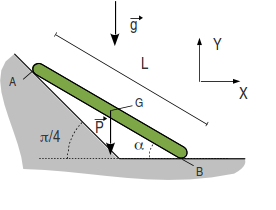
La barra de la figura forma un ángulo $α$ con la horizontal y está apoyada sobre una pared inclinada $π / 4$ . El peso de la barra está aplicado en su centro. El contacto en el punto $A$ es liso, mientras que en el punto $B$ es rugoso con un coeficiente de rozamiento estático $μ$ .

Dibuja el diagrama de sólido libre de la barra.
Considerando el ángulo $α$ como un dato, calcula las fuerzas sobre la barra en los puntos $A$ y $B$ .
¿Para que valores del ángulo $α$ es posible el equilibrio?

2 Solución

2.1 Diagrama de sólido libre

El contacto en A es liso, por lo que la fuerza de reacción vincular es normal a la superficie. El contacto en B es rugoso, es decir, en B actúa una fuerza de reacción vincular normal al suelo y una fuerza de rozamiento paralelo a él. En el dibujo hemos usado el teorema de las tres fuerzas. Agrupando la fuerza de reacción vincular y de rozamiento en B, la barra está sometida a tres fuerzas coplanarias, por lo que sus rectas soporte deben cruzarse en un punto.

2.2 Fuerzas en equilibrio

Cuando la barra está en equilibrio la fuerza neta sobre ella es cero y el momento neto es nulo respecto a cualquier punto. Una vez que hemos identificado las fuerzas sobre la barra, buscamos su expresión en el sistema de ejes que hemos escogido. Tenemos

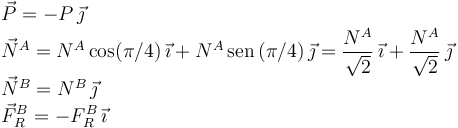
$\begin{array}{l} \vec{P} = -P\,\vec{\jmath} \\ \vec{N}^A =N^A\cos(\pi/4)\,\vec{\imath} + N^A\,\mathrm{sen}\,(\pi/4)\,\vec{\jmath} = \dfrac{N^A}{\sqrt{2}}\,\vec{\imath} + \dfrac{N^A}{\sqrt{2}}\,\vec{\jmath} \\ \vec{N}^B = N^B\,\vec{\jmath} \\ \vec{F}_R^B = -F_R^B\,\vec{\imath} \end{array}$

Aplicamos la condición de que la fuerza neta es nula

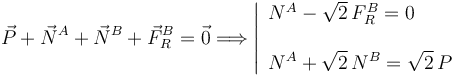
$\vec{P} + \vec{N}^A + \vec{N}^B + \vec{F}_R^B = \vec{0} \Longrightarrow \left| \begin{array}{l} N^A - \sqrt{2}\,F_R^B = 0 \\ \\ N^A + \sqrt{2}\,N^B = \sqrt{2}\,P \end{array} \right.$

Ahora calculamos los momentos de las fuerzas respecto a B. Las únicas fuerzas con momento no nulo son el peso y 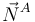$\vec{N}^A$ .

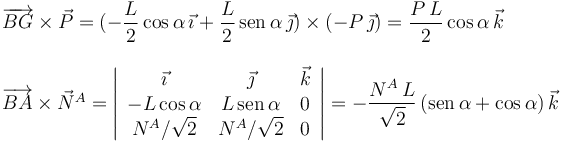
$\begin{array}{l} \overrightarrow{BG}\times\vec{P} = (-\dfrac{L}{2}\cos\alpha\,\vec{\imath} + \dfrac{L}{2}\,\mathrm{sen}\,\alpha\,\vec{\jmath})\times(-P\,\vec{\jmath}) = \dfrac{P\,L}{2}\cos\alpha\,\vec{k} \\ \\ \overrightarrow{BA}\times\vec{N}^A = \left| \begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ -L\cos\alpha & L\,\mathrm{sen}\,\alpha & 0 \\ N^A/\sqrt{2} & N^A/\sqrt{2} & 0 \end{array} \right| = -\dfrac{N^A\,L}{\sqrt{2}}\,(\mathrm{sen}\,\alpha + \cos\alpha)\,\vec{k} \end{array}$

La suma de estos dos momentos debe ser nula

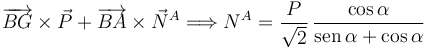
$\overrightarrow{BG}\times\vec{P} + \overrightarrow{BA}\times\vec{N}^A \Longrightarrow N^A = \dfrac{P}{\sqrt{2}}\,\dfrac{\cos\alpha}{\mathrm{sen}\,\alpha + \cos\alpha}$

Introduciendo esta expresión en las ecuaciones obtenidas previamente, tenemos

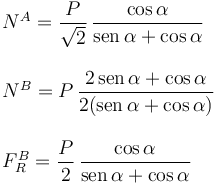
$\begin{array}{l} N^A = \dfrac{P}{\sqrt{2}}\,\dfrac{\cos\alpha}{\mathrm{sen}\,\alpha + \cos\alpha} \\ \\ N^B = P\,\dfrac{2\,\mathrm{sen}\,\alpha + \cos\alpha}{2(\mathrm{sen}\,\alpha + \cos\alpha)} \\ \\ F^B_R = \dfrac{P}{2}\,\dfrac{\cos\alpha}{\mathrm{sen}\,\alpha+\cos\alpha} \end{array}$

2.3 Análisis del equilibrio

El equilibrio se rompe cuando el extremo en B desliza. Para que esto no ocurra la fuerza de rozamiento necesaria para mantener el equilibrio debe ser menor o igual que su valor máximo. Si el coeficiente de rozamiento estático es $μ$ tenemos

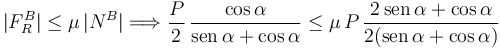
$|F_R^B| \leq \mu\,|N^B| \Longrightarrow \dfrac{P}{2}\,\dfrac{\cos\alpha}{\mathrm{sen}\,\alpha+\cos\alpha} \leq \mu\,P\,\dfrac{2\,\mathrm{sen}\,\alpha + \cos\alpha}{2(\mathrm{sen}\,\alpha + \cos\alpha)}$

Operando llegamos a la condición

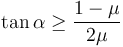
$\tan\alpha \geq \dfrac{1-\mu}{2\mu}$

Esta condición puede escribirse así

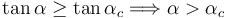
$\tan{\alpha} \geq \tan\alpha_c \Longrightarrow \alpha>\alpha_c$

con

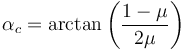
$\alpha_c = \arctan\left(\dfrac{1-\mu}{2\mu}\right)$

El ángulo $α$ es mayor que cero y menor que $π / 4$ . Para que pueda existir equilibrio, el valor de $α c$ debe ser menor que el mayor valor posible de $α$ . Eso marca un valor mínimo del coeficiente de rozamiento estático

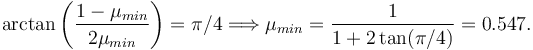
$\arctan\left(\dfrac{1-\mu_{min}}{2\mu_{min}}\right) = \pi/4 \Longrightarrow \mu_{min} = \dfrac{1}{1+2\tan(\pi/4)} = 0.547.$

Si $μ < μ m i n$ no hay equilibrio para ningún ángulo.

Por otra parte, si $α c = 0$ , habría equilibrio para todos los valores posibles de $α$ . El coeficiente de rozamiento estático para $α c = 0$ es

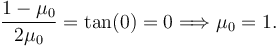
$\dfrac{1-\mu_0}{2\mu_0} = \tan(0) = 0 \Longrightarrow \mu_0 = 1.$

Es decir, si 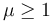$\mu\geq 1$ todos los valores de $α$ entre 0 y $π / 4$ son de equilibrio.

Barra apoyada sobre una pared inclinada, Diciembre 2012 (G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Diagrama de sólido libre

2.2 Fuerzas en equilibrio

2.3 Análisis del equilibrio

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES