De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

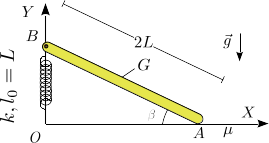
Una barra homogénea de masa $m$ y longitud $2 L$ está apoyada en el suelo en un extremo (punto $A$ ). El otro extremo ( $B$ ) está articulado en un eje vertical de modo que la barra puede rotar alrededor de $B$ y el punto $B$ puede deslizar sobre el eje. Un muelle de constante elástica $k$ y longitud natural $L$ conecta el punto $B$ con el origen de coordenadas $O$ . El muelle se mantiene vertical en todo momento. El contacto de la barra en $B$ es liso, mientras que es rugoso en $A$ con coeficiente estático de rozamiento $μ$ .

Dibuja el diagrama de cuerpo libre de la barra, indicando para que fuerzas el sentido es conocido a priori y para cuales no. Razona la respuesta.
Escribe las expresiones de las fuerzas que actúan sobre la barra.
Suponiendo que $β = π / 6$ , calcula el valor de las fuerzas que actúan sobre la barra en situación de equilibrio estático.
Calcula la reducción vincular en el punto $G$ usando las fuerzas obtenidas en el apartado anterior.
¿Qué condición debe cumplir $μ$ para que la situación de equilibrio sea posible?

2 Solución

2.1 Diagrama de cuerpo libre

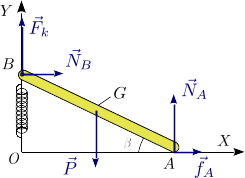
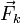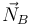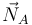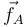La figura de la derecha muestra las fuerzas que actúan sobre la barra. Las fuerzas activas son su peso, $\vec{P}$ , y la fuerza del muelle, $\vec{F}_k$ . Las fuerzas de reacción vincular son la normal en $B$ , $\vec{N}_B$ , la normal en $A$ , $\vec{N}_A$ , y la fuerza de rozamiento en $A$ , $\vec{f}_A$ .

Sabemos a priori que el peso apunta hacia abajo y que la normal en $A$ apunta hacia arriba. No conocemos a priori el sentido de las otras fuerzas. El sentido de la fuerza del muelle depende de su elongación. El vínculo en $B$ es bilateral, puede apuntar en los dos sentidos. Por eso, no conocemos el sentido de la fuerza de rozamiento en $A$ , pues esta fuerza es la única que compensa a 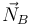$\vec{N}_B$ .

2.2 Expresiones de las fuerzas

Usando la base del triedro de la figura tenemos

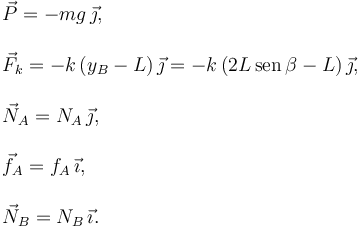
$\begin{array}{l} \vec{P} = -mg\,\vec{\jmath},\\ \\ \vec{F}_k = -k\,(y_B-L)\,\vec{\jmath} = -k\,(2L\,\mathrm{sen}\,\beta-L)\,\vec{\jmath},\\ \\ \vec{N}_A = N_A\,\vec{\jmath},\\ \\ \vec{f}_A = f_A\,\vec{\imath},\\ \\ \vec{N}_B = N_B\,\vec{\imath}. \end{array}$

2.3 Equilibrio con $β = π / 6$

Las condiciones de equilibrio son que la suma neta de fuerzas es cero y que el momento de fuerzas neto es cero.

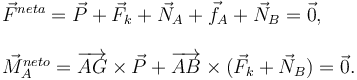
$\begin{array}{l} \vec{F}^{neta} = \vec{P} + \vec{F}_k + \vec{N}_A + \vec{f}_A + \vec{N}_B = \vec{0},\\ \\ \vec{M}_A^{neto} = \overrightarrow{AG}\times\vec{P} + \overrightarrow{AB}\times(\vec{F}_k + \vec{N}_B)=\vec{0}. \end{array}$

Hemos calculado los momentos respecto de $A$ pero puede ser cualquier otro punto.

El enunciado nos dice que $β = π / 6$ . Entonces la fuerza elástica es

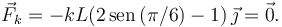
$\vec{F}_k = -kL(2\,\mathrm{sen}\,(\pi/6) - 1)\,\vec{\jmath} = \vec{0}.$

Podemos pues quitar la fuerza del muelle de las ecuaciones.

La primera condición nos da 2 ecuaciones

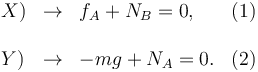
$\begin{array}{lclr} X) & \to & f_A + N_B = 0, & (1)\\ &&&\\ Y) & \to & -mg + N_A=0. & (2) \end{array}$

Para calcular el momento neto hacemos los productos vectoriales. Usamos otra vez que $β = π / 6$

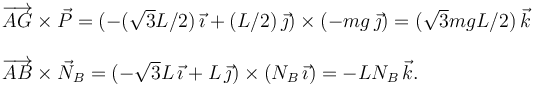
$\begin{array}{l} \overrightarrow{AG}\times\vec{P} = (-(\sqrt{3}L/2)\,\vec{\imath} + (L/2)\,\vec{\jmath}) \times(-mg\,\vec{\jmath}) = (\sqrt{3}mgL/2)\,\vec{k} \\ \\ \overrightarrow{AB}\times\vec{N}_B = (-\sqrt{3}L\,\vec{\imath} + L\,\vec{\jmath}) \times(N_B\,\vec{\imath}) = -LN_B\,\vec{k}. \end{array}$

El momento neto es

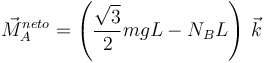
$\vec{M}_A^{neto} = \left( \dfrac{\sqrt{3}}{2}mgL -N_BL \right)\,\vec{k}$

Como tiene que ser nulo obtenemos la ecuación

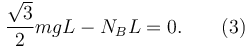
$\dfrac{\sqrt{3}}{2}mgL -N_BL = 0. \qquad (3)$

Tenemos 3 ecuaciones para 3 incógnitas: ${N A, f A, N B}$ . Resolviéndolas obtenemos

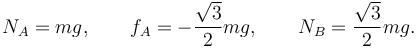
$N_A = mg, \qquad f_A = -\dfrac{\sqrt{3}}{2}mg, \qquad N_B = \dfrac{\sqrt{3}}{2}mg.$

Los vectores son

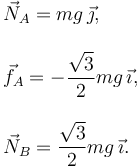
$\begin{array}{l} \vec{N}_A = mg\,\vec{\jmath}, \\ \\ \vec{f}_A = -\dfrac{\sqrt{3}}{2}mg\,\vec{\imath},\\ \\ \vec{N}_B = \dfrac{\sqrt{3}}{2}mg\,\vec{\imath}. \end{array}$

2.4 Reducción vincular en $G$

Las fuerzas vinculares son 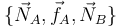$\{\vec{N}_A, \vec{f}_A, \vec{N}_B\}$ . La resultante es

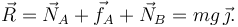
$\vec{R} = \vec{N}_A + \vec{f}_A + \vec{N}_B = mg\,\vec{\jmath}.$

El momento resultante en $G$ es

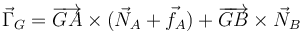
$\vec{\Gamma}_G = \overrightarrow{GA}\times(\vec{N}_A+\vec{f}_A) + \overrightarrow{GB}\times\vec{N}_B$

Podemos calcularlo así. Pero es más rápido de esta forma. El momento neto respecto a $G$ tiene que ser cero, para que haya equilibrio. Esto quiere decir que el momento vincular y el dinámico (el de las fuerzas activas) tienen que anularse

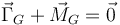
$\vec{\Gamma}_G + \vec{M}_G = \vec{0}$

Y el momento dinámico es

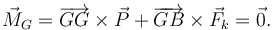
$\vec{M}_G = \overrightarrow{GG}\times\vec{P} + \overrightarrow{GB}\times\vec{F}_k = \vec{0}.$

El primer término es nulo por que 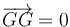$\overrightarrow{GG}=0$ . El segundo es nulo porque para este valor de $β$ la fuerza del muelle es nula. Por tanto la reducción vincular es

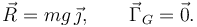
$\vec{R} = mg\,\vec{\jmath}, \qquad \vec{\Gamma}_G=\vec{0}.$

2.5 Condición de equilibrio

La condición para que el rozamiento en $A$ sea capaz de equilibrar la barra es

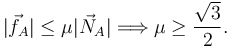
$|\vec{f}_A| \leq \mu|\vec{N}_A| \Longrightarrow \mu \geq \dfrac{\sqrt{3}}{2}.$

2.6 Errores comunes detectados en la corrección

La fuerza vincular en $B$ tiene únicamente componente horizontal, porque ese es el movimiento prohibido por el vínculo. El punto $B$ se puede mover verticalmente a lo largo de la barra sin restricciones, por tanto no hay componente de fuerza vincular en la dirección vertical.
La longitud natural del muelle no es nula. Hay que usar la expresión adecuada para describir la fuerza que ejerce.

Barra articulada en pared con muelle (Sep. 2018 G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Diagrama de cuerpo libre

2.2 Expresiones de las fuerzas

2.3 Equilibrio con $β = π / 6$

2.4 Reducción vincular en $G$

2.5 Condición de equilibrio

2.6 Errores comunes detectados en la corrección

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

Barra articulada en pared con muelle (Sep. 2018 G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Diagrama de cuerpo libre

2.2 Expresiones de las fuerzas

2.3 Equilibrio con β = π / 6

2.4 Reducción vincular en G

2.5 Condición de equilibrio

2.6 Errores comunes detectados en la corrección

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

2.3 Equilibrio con $β = π / 6$

2.4 Reducción vincular en $G$