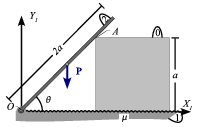
Varilla apoyada sobre un cuadrado con contacto rugoso
De Laplace
Contenido |
1 Enunciado
El esquema de la figura muestra una placa cuadrada de lado a y espesor y peso despreciables (sólido "0"). Ésta se halla contenida en un plano vertical OX1Y1, con uno de sus lados en contacto con el eje horizontal OX1 (sólido "1"). Dicho contacto es rugoso, con un coeficiente de rozamiento estático μ. Al mismo tiempo, sobre el vértice A de la placa se apoya una varilla pesada y homogénea, de peso P y longitud 2a (sólido "2"), con un contacto liso. La varilla se mantiene siempre en el plano vertical OX1Y1, y puede girar libremente alrededor de su extremo articulado sin rozamiento en el punto O del eje horizontal fijo. Se pide:
- Fragmentar el sistema de sólidos y representar sus correspondientes "diagramas de sólido libre".
- El rango de valores del parámetro θ para el que es posible el equilibrio estático del sistema, y las reacciones vinculares ejercidas sobre la varilla en dicha situación.
2 Solución
2.1 Diagrama de sólido libre
Los contactos en A y O son lisos, mientras que el contacto de la
base de la placa con el suelo es rugoso. Este último es un contacto
distribuido, es decir, hay una distribución de fuerzas paralelas
actuando sobre la base de la placa. Este sistema puede reducirse en su
centro(punto B en la figura), donde se sitúa su resultante
(fuerza 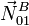 ). Además,
el carácter rugoso del contacto hace que aparezca una fuerza
). Además,
el carácter rugoso del contacto hace que aparezca una fuerza
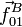 proporcional a la resultante del sistema de fuerzas
paralelas. La fuerza de reacción vincular
proporcional a la resultante del sistema de fuerzas
paralelas. La fuerza de reacción vincular
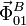 es la suma de estas dos fuerzas. La figura de la izquierda muestra las fuerzas que actúan
sobre los sólidos "2" y "0". Para que el equilibrio pueda
producirse el punto B debe estar dentro de la base de
la placa.
es la suma de estas dos fuerzas. La figura de la izquierda muestra las fuerzas que actúan
sobre los sólidos "2" y "0". Para que el equilibrio pueda
producirse el punto B debe estar dentro de la base de
la placa.
En el dibujo, la dirección de la fuerza 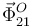 en la
articulación se determina aplicando el teorema de las tres fuerzas al
sólido "2".
en la
articulación se determina aplicando el teorema de las tres fuerzas al
sólido "2".
2.2 Condición de equilibrio
Los vectores de posición de los puntos relevantes en el problema son
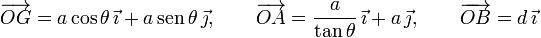
A partir de la figura, las expresiones de las diferentes fuerzas que actúan sobre cada sólido son
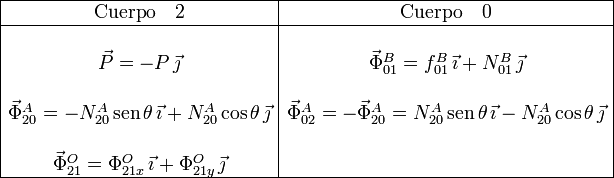
Podemos determinar 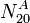 imponiendo que el momento total sobre el
sólido "2" es nulo. Calculando este momento en O evitamos tener
que detallar la fuerza
imponiendo que el momento total sobre el
sólido "2" es nulo. Calculando este momento en O evitamos tener
que detallar la fuerza 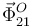 . Tenemos
. Tenemos
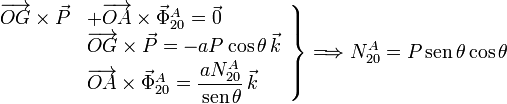
Ahora podemos calcular 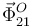 imponiendo que la suma
de fuerzas sobre la varilla sea nula
imponiendo que la suma
de fuerzas sobre la varilla sea nula
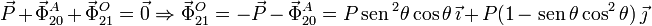
Ahora aplicamos que la suma de fuerzas sobre la placa también debe ser cero en el equilibrio
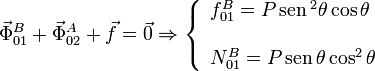
El módulo de la fuerza de rozamiento es 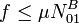 . Por tanto,
para que el equilibrio sea posible debe cumplirse
. Por tanto,
para que el equilibrio sea posible debe cumplirse
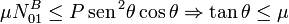
Si θ es mayor que ese valor límite, la placa desliza hacia la derecha.
Pero el equilibrio también puede romperse por el vuelco de la placa. Para estudiarlo examinamos la condición de que el momento resultante de las fuerzas aplicadas sobre la placa sea nulo. Escogemos el punto O para calcular el momento
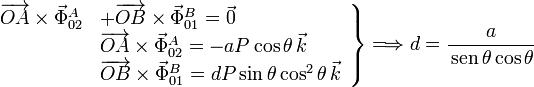
Para que la placa no vuelque el punto B debe estar dentro de su base, es decir, debe cumplirse
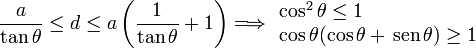
La primera condición se cumple siempre, pues
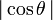 es siempre menor que uno. Esto quiere decir que el punto B
nunca va a salirse de la base hacia el punto O, es decir, el bloque
nunca va a volcar hacia la izquierda.
es siempre menor que uno. Esto quiere decir que el punto B
nunca va a salirse de la base hacia el punto O, es decir, el bloque
nunca va a volcar hacia la izquierda.