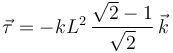De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

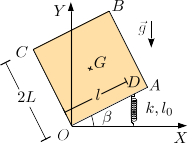
Una placa cuadrada homogénea de masa $m$ y lado $2 L$ se apoya sobre uno de sus extremos, el punto $O$ de la figura. Este vértice de la placa no se mueve nunca. Un muelle de constante elástica $k$ y longitud natural $l 0 = L$ está conectado a un punto $D$ del lado $O A$ de la placa. El otro extremo del muelle está en el eje $O X$ , de modo que el muelle es siempre vertical. La gravedad actúa como se indica en la figura. La masa de la placa es tal que $m g = k L$ .

Dibuja el diagrama de cuerpo libre del sólido rígido.
Encuentra las expresiones de las fuerzas que actúan sobre la placa.
Si tenemos $β = π / 3$ , encuentra el valor de $l$ para el que la placa está en equlibrio.
Suponiendo que $β = π / 4$ , calcula el par de fuerzas que habría que aplicar sobre la placa para que esté en equilibrio cuando el punto $D$ coincide con el $A$ (el muelle siempre está vertical). Encuentra también el valor de las fuerzas vinculares en esta situación.

2 Solución

2.1 Diagrama de cuerpo libre y expresiones de las fuerzas

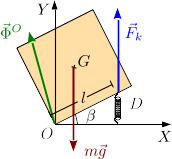
El diagrama de la derecha muestra las tres fuerzas que actúan sobre la placa: el peso, la fuerza del muelle y la fuerza vincular en $O$ . La expresión de estas fuerzas es

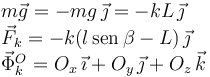
$\begin{array}{l} m\vec{g} = -mg\,\vec{\jmath}= -kL\,\vec{\jmath} \\ \vec{F}_k = -k(l\,\mathrm{sen}\,\beta - L)\,\vec{\jmath}\\ \vec{\Phi}^O_{k} = O_x\,\vec{\imath} + O_y\,\vec{\jmath} + O_z\,\vec{k} \end{array}$

La fuerza vincular tiene tres componentes no nulas a priori pues el punto $O$ no puede moverse. Hemos usado que, según el enunciado, $m g = k L$ .

2.2 Equilibrio con $β = π / 3$

Las condiciones de equilibrio son fuerza neta nula y momento de fuerzas respecto a cualquier punto nulo. De la primera condición obtenemos

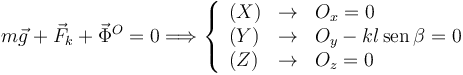
$m\vec{g} + \vec{F}_k + \vec{\Phi}^O=0 \Longrightarrow \left\{ \begin{array}{lcl} (X) & \to & O_x = 0\\ (Y) & \to & O_y - kl\,\mathrm{sen}\,\beta = 0\\ (Z) & \to & O_z=0 \end{array} \right.$

Calculamos los momentos de las fuerzas respecto a $O$ :

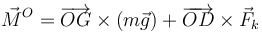
$\vec{M}^O = \overrightarrow{OG}\times(m\vec{g}) + \overrightarrow{OD}\times\vec{F}_k$

La fuerza vincular no ejerce momento respecto a $O$ . Tenemos

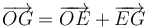
$\overrightarrow{OG} = \overrightarrow{OE} + \overrightarrow{EG}$

De la figura vemos que

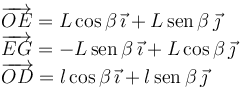
$\begin{array}{l} \overrightarrow{OE} = L\cos\beta\,\vec{\imath} + L\,\mathrm{sen}\,\beta\,\vec{\jmath} \\ \overrightarrow{EG} = -L\,\mathrm{sen}\,\beta\,\vec{\imath} + L\cos\beta\,\vec{\jmath} \\ \overrightarrow{OD} = l\cos\beta\,\vec{\imath} + l\,\mathrm{sen}\,\beta\,\vec{\jmath} \end{array}$

Por tanto

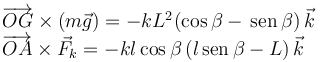
$\begin{array}{l} \overrightarrow{OG}\times(m\vec{g}) = -kL^2(\cos\beta-\,\mathrm{sen}\,\beta)\,\vec{k} \\ \overrightarrow{OA}\times\vec{F}_k = -kl\cos\beta\,(l\,\mathrm{sen}\,\beta - L)\,\vec{k} \end{array}$

Imponiendo la condición de equilibrio 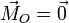$\vec{M}_O=\vec{0}$ obtenemos la ecuación

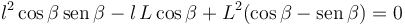
$l^2\cos\beta\,\mathrm{sen}\,\beta - l\,L\cos\beta + L^2(\cos\beta-\mathrm{sen}\,\beta) = 0$

En el caso $β = π / 3$ tenemos

$\cos\beta = 1/2, \qquad \mathrm{sen}\,\beta=\sqrt{3}/2$

Resolviendo la ecuación de segundo grado, nos quedamos con la solución positiva

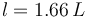
$l = 1.66\,L$

La fuerza vincular es

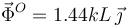
$\vec{\Phi}^O = 1.44 kL \,\vec{\jmath}$

2.3 Par de fuerzas cuando el muelle está en $A$ y $β = π / 4$

Ahora hay que añadir un par de fuerzas externo en la condición de momento nulo. Tenemos

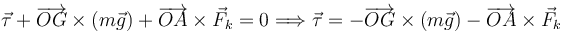
$\vec{\tau} + \overrightarrow{OG}\times(m\vec{g}) + \overrightarrow{OA}\times\vec{F}_k = 0 \Longrightarrow \vec{\tau} = - \overrightarrow{OG}\times(m\vec{g}) - \overrightarrow{OA}\times\vec{F}_k$

Cuando $β = π / 4$ tenemos

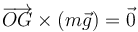
$\overrightarrow{OG}\times(m\vec{g}) = \vec{0}$

Si el extremo del muelle está en $A$ y $β = π / 4$ el par que ejerce el muelle es

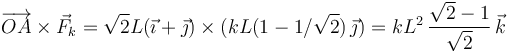
$\overrightarrow{OA}\times\vec{F}_k = \sqrt{2}L(\vec{\imath} + \vec{\jmath})\times(kL(1-1/\sqrt{2})\,\vec{\jmath}) = kL^2\,\dfrac{\sqrt{2}-1}{\sqrt{2}}\,\vec{k}$

Por tanto el par que hay que aplicar es

$\vec{\tau} = -kL^2\,\dfrac{\sqrt{2}-1}{\sqrt{2}}\,\vec{k}$

Placa cuadrada pivotando conectada a un muelle, Sept 2017 (G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Diagrama de cuerpo libre y expresiones de las fuerzas

2.2 Equilibrio con $β = π / 3$

2.3 Par de fuerzas cuando el muelle está en $A$ y $β = π / 4$

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

Placa cuadrada pivotando conectada a un muelle, Sept 2017 (G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Diagrama de cuerpo libre y expresiones de las fuerzas

2.2 Equilibrio con β = π / 3

2.3 Par de fuerzas cuando el muelle está en A y β = π / 4

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

2.2 Equilibrio con $β = π / 3$

2.3 Par de fuerzas cuando el muelle está en $A$ y $β = π / 4$