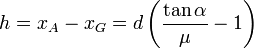Varilla en dos puntos con contacto rugoso

De Laplace

Contenido

1 Enunciado
2 Solución
- 2.1 Diagrama de sólido libre
- 2.2 Equilibrio mecánico

1 Enunciado

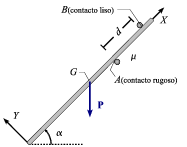
La barra homogénea de la figura tiene peso $P$ y se halla en equilibrio, si bien en situación de "deslizamiento inminentei", como consecuencia de haber quedado encajada entre los soportes puntuales $A$ (contacto rugoso de coeficiente de rozamiento estático $μ$ ) y $B$ (contacto liso). Conocidos el ángulo $α$ de inclinación de la barra con respecto a la horizontal, así como la distancia $d$ que separa a los dos soportes puntuales, se pide:

Desvincular razonadamente la barra ("diagrama de sólido libre")
Determinar la distancia $(x A - x G$ ) entre el centro de gravedad $G$ de la barra y el soporte puntual $A$ .
Calcular las reacciones vinculares ejercidas sobre la barra por los soportes puntuales $A$ y $B$ .

2 Solución

2.1 Diagrama de sólido libre

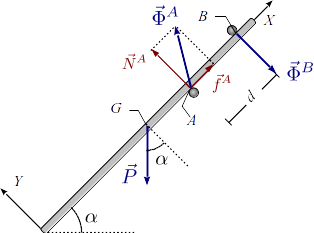
El contacto en $B$ es liso, por lo que la fuerza de reacción es perpendicular a la varilla. Por otro lado, el contacto en $A$ es rugoso, por lo que la fuerza de reacción tiene una componente normal y una tangencial a la varilla. Las expresiones de las fuerzas en el sistema de ejes propuesto es

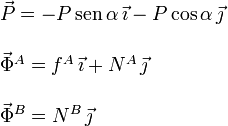
$\begin{array}{l} \vec{P} = -P\,\mathrm{sen}\,\alpha\,\vec{\imath}-P\cos\alpha\,\vec{\jmath}\\ \\ \vec{\Phi}^A = f^A\,\vec{\imath}+N^A\,\vec{\jmath}\\ \\ \vec{\Phi}^B = N^B\,\vec{\jmath} \end{array}$

No imponemos el signo de las fuerzas, sino que vendrá dado por el cálculo. La figura muestra la desvinculación de la varilla.

2.2 Equilibrio mecánico

Las condiciones de equilibrio son que la resultante y el momento resultante en cualquier punto del sistema de fuerzas que actúan sobre la varilla deben ser ambos nulos. De la suma de fuerzas obtenemos

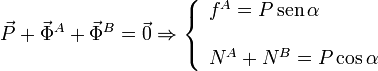
$\vec{P}+\vec{\Phi}^A+\vec{\Phi}^B =\vec{0}\Rightarrow \left\{ \begin{array}{l} f^A = P\,\mathrm{sen}\,\alpha \\ \\ N^A + N^B = P\cos\alpha \end{array} \right.$

Escogemos el punto $G$ para calcular el momento. Vamos a llamar $h = x A - x G$ . Tenemos

$\begin{array}{rl} \overrightarrow{GA}\times\vec{\Phi}^A&+\overrightarrow{GB}\times\vec{\Phi}^B=\vec{0} \\ &\overrightarrow{GA}\times\vec{\Phi}^A = (h\,\vec{\imath})\times(f^A\,\vec{\imath}+N^A\,\vec{\jmath})=h\,N^A,\vec{k}\\ &\overrightarrow{AB}\times\vec{\Phi}^B = [(d+h)\,\vec{\imath}]\times(N^B\,\vec{\jmath})= (d+h)\,N^B\,\vec{k} \end{array}$

La suma debe ser cero por lo que obtenemos

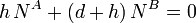
$h\,N^A + (d+h)\,N^B = 0$

Junto con las dos ecuaciones anteriores obtenemos los valores de las f.r.v. en los puntos $A$ y $B$

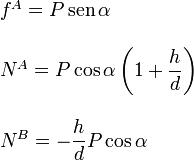
$\left. \begin{array}{l} f^A = P\,\mathrm{sen}\,\alpha\\ \\ N^A = P\cos\alpha\left(1+\dfrac{h}{d}\right)\\ \\ N^B = -\dfrac{h}{d}P\cos\alpha \end{array} \right.$

Para que haya equilibrio frente a deslizamiento $f A$ debe ser capaz de alcanzar el valor obtenido aquí. Pero el valor de $f A$ está limitado por el coeficiente de rozamiento. Para que haya equilibrio debe cumplirse que

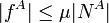
$|f^A|\leq \mu|N^A|$

El problema nos dice que estamos en condiciones de deslizamiento inminente. En este caso límite tenemos

| f A | = μ | N A |

Aplicando esta condición llegamos a

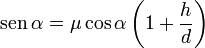
$\,\mathrm{sen}\,\alpha = \mu\cos\alpha\left(1+\dfrac{h}{d}\right)$

A partir de aquí podemos obtener la distancia $h$ en función de los otros parámetros

$h= x_A-x_G=d\left(\dfrac{\tan\alpha}{\mu}-1\right)$

Varilla en dos puntos con contacto rugoso

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Diagrama de sólido libre

2.2 Equilibrio mecánico

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES