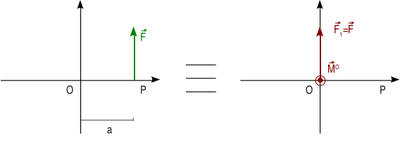
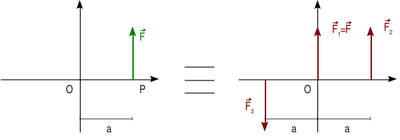
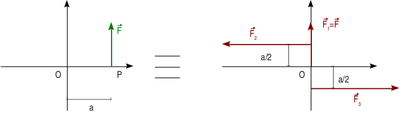
Sistema de vectores deslizantes equivalente a un vector deslizante

De Laplace

1 Enunciado

Una fuerza 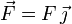$\vec{F} = F\,\vec{\jmath}$ actúa sobre un sólido rígido aplicada en el punto $P (a,0,0)$ . Encuentra un sistema de vectores deslizantes formado por tres fuerzas que sea equivalente a la fuerza $\vec{F}$ y esté aplicado en el origen de referencia.

2 Solución

Dado un vector deslizante aplicado en un punto $P$ , su efecto es el mismo que el de un sistema de vectores deslizantes aplicado en un punto $O$ y compuesto por el mismo vector original más un par de vectores, cuyo momento debe ser el mismo que el del vector original respecto al punto $O$ .

El vector deslizante del enunciado es

$\vec{F}=F\,\vec{\jmath}\qquad\qquad P(a,0,0)$

El momento de este vector respecto del punto $O$ es

$\vec{M}^O = \overrightarrow{OP}\times\vec{F}= (a\,\vec{\imath})\times(F\,\vec{\jmath})= aF\,\vec{k}$

El sistema equivalente está formado por el mismo vector original aplicado en $O$ y un par de vectores

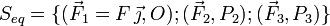
$S_{eq} = \{ (\vec{F}_1=F\,\vec{\jmath},O); (\vec{F}_2,P_2); (\vec{F}_3, P_3)\}$

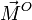Con la condición $\vec{F}_2=-\vec{F}_3$ ya que forman un par de vectores. El momento de este par debe ser igual que $\vec{M}^O$ .

Hay infinitos pares de vectores que tienen este momento. Basta con que el producto del brazo del par por el módulo de sus vectores sea $a F$ , y que la dirección y sentido sean los mismos. Una posibilidad es el par de vectores deslizantes

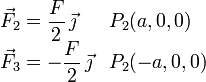
$\begin{array}{ll} \vec{F}_2 = \dfrac{F}{2}\,\vec{\jmath} & P_2(a,0,0)\\ \vec{F}_3 = -\dfrac{F}{2}\,\vec{\jmath} & P_2(-a,0,0) \end{array}$

En este caso el brazo del par es $2 a$ y el módulo de los vectores es $F / 2$

Otra posibilidad es la de la figura. En este caso el brazo del par es $a$ y el módulo de los vectores es $F$ .

Sistema de vectores deslizantes equivalente a un vector deslizante

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES