Varilla con peso y muelle horizontal

De Laplace

Contenido

1 Enunciado
2 Solución
- 2.1 Diagrama de sólido libre
- 2.2 Determinación del ángulo de equilibrio

1 Enunciado

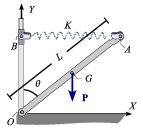
La varilla $O A$ , homogénea, de peso $P$ y longitud $L$ , está obligada a permanecer en el plano vertical fijo $O X Y$ . Su extremo $O$ se halla articulado al origen del sistema de referencia, mientras que su extremo $A$ está conectado, mediante un resorte elástico ideal de constante recuperadora $K$ y longitud natural nula, a un deslizador puntual $B$ que puede moverse sin rozamiento a lo largo del eje $O Y$ . El resorte $A B$ se mantiene perpendicular al eje $O Y$ en todo instante.

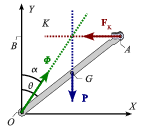
Representa el "diagrama de sólido libre" de la varilla teniendo en cuenta el teorema de las tres fuerzas.
Determina el ángulo $θ$ que forma la varilla con el eje vertical $O Y$ en la posición de equilibrio (descartando las soluciones $θ = 0$ y $θ = π$ radianes)

2 Solución

2.1 Diagrama de sólido libre

Tenemos que desvincular la varilla, de modo que cada vínculo se sustituye por una fuerza de reacción vincular. Analicemos las fuerzas que actúan sobre la varilla

Peso: se aplica en el centro de gravedad $G$ de la varilla y apunta hacia abajo, por tanto

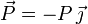
$\vec{P}=-P\,\vec{\jmath}$

Muelle: el muelle está siempre en posición horizontal y su longitud natural es nula. Por tanto la fuerza que ejerce es proporcional a la distancia entre el punto $A$ y el punto de sujeción $B$ y apunta hacia este último

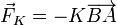
$\vec{F}_K = -K\overrightarrow{BA}$

Fuerza de reacción vincular: está aplicada en la articulación en $O$ . Esta articulación impide la traslación de la varilla tanto en la dirección $X$ como en la $Y$ . Por tanto la fuerza de reacción tiene componentes en esas dos direcciones

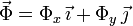
$\vec{\Phi}=\Phi_x\,\vec{\imath}+\Phi_y\,\vec{\jmath}$

Ahora bien, el teorema de las tres fuerzas nos dice que si el sólido está en equilibrio las rectas soportes de las tres fuerzas necesariamente se cortan en un punto (siempre que no sean paralelas entre sí). Como conocemos la dirección del peso y de la fuerza recuperadora del muelle podemos determinar gráficamente la dirección de la fuerza de reacción vincular, como se indica en la figura.

2.2 Determinación del ángulo 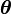$\boldsymbol{\theta}$ de equilibrio

Para que un sólido rígido esté en equilibrio mecánico las fuerzas que actúan sobre él deben cumplir dos condiciones, que la suma total de fuerzas sea cero y que el momento resultante respecto a cualquier punto sea también en cero. Si escogemos el punto $O$ para calcular el momento estas condiciones se expresan como

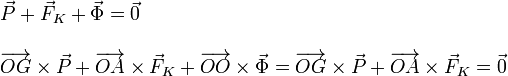
$\begin{array}{l} \vec{P}+\vec{F}_K+\vec{\Phi}=\vec{0}\\ \\ \overrightarrow{OG}\times\vec{P}+\overrightarrow{OA}\times\vec{F}_K+\overrightarrow{OO}\times\vec{\Phi}=\overrightarrow{OG}\times\vec{P}+\overrightarrow{OA}\times\vec{F}_K=\vec{0} \end{array}$

En la suma de momentos el par correspondiente a $\vec{\Phi}$ se anula pues se calcula respecto a su punto de aplicación.

En este problema podemos determinar el ángulo aplicando directamente la condición de momento resultante nulo. Al escoger el punto $O$ para calcular el momento nos quitamos de en medio la fuerza $\vec{\Phi}$ . Necesitamos expresar en función del ángulo $θ$ los vectores necesarios para calcular este momento. Son

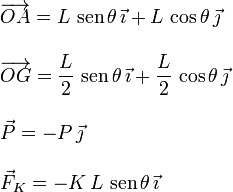
$\begin{array}{l} \overrightarrow{OA} = L\,\,\mathrm{sen}\,\theta\,\vec{\imath}+L\,\cos\theta\,\vec{\jmath}\\ \\ \overrightarrow{OG} = \dfrac{L}{2}\,\,\mathrm{sen}\,\theta\,\vec{\imath}+\dfrac{L}{2}\,\cos\theta\,\vec{\jmath}\\ \\ \vec{P} = -P\,\vec{\jmath}\\ \\ \vec{F}_K = -K \,L\,\,\mathrm{sen}\,\theta\,\vec{\imath} \end{array}$

Los momentos que necesitamos son

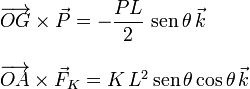
$\begin{array}{l} \overrightarrow{OG}\times\vec{P}=-\dfrac{PL}{2}\,\,\mathrm{sen}\,\theta\,\vec{k}\\ \\ \overrightarrow{OA}\times\vec{F}_K=K\,L^2\,\mathrm{sen}\,\theta\cos\theta\,\vec{k} \end{array}$

La suma debe ser cero, de donde obtenemos tres posibles soluciones

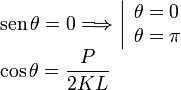
$\begin{array}{l} \mathrm{sen}\,\theta=0\Longrightarrow \left| \begin{array}{l} \theta=0\\ \theta=\pi \end{array} \right. \\ \cos\theta = \dfrac{P}{2KL} \end{array}$

La solución para el coseno no puede ser válida siempre. Si el peso es mayor que $2 K L$ esa solución no puede aparecer, pues el coseno de un ángulo no puede ser mayor que uno.

Cuando se analiza la estabilidad de las soluciones (con técnicas que no hemos visto en clase), resulta que la solución que involucra al $cosθ$ es inestable, es decir, no se va a observar nunca en la práctica. Si $P < 2 K L$ , las dos soluciones $θ = 0$ y $θ = π$ son estables. Cuál de ellas se observa depende del valor inicial del ángulo. Si es menor que $arccos(P / 2 K L)$ se observa la solución $θ = 0$ . Si es mayor que ese valor se observa $θ = π$ .

Por otro lado, si $P > 2 K L$ la única solución estable es $θ = π$ .

Varilla con peso y muelle horizontal

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Diagrama de sólido libre

2.2 Determinación del ángulo $\boldsymbol{\theta}$ de equilibrio

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

Varilla con peso y muelle horizontal

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Diagrama de sólido libre

2.2 Determinación del ángulo de equilibrio

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

2.2 Determinación del ángulo $\boldsymbol{\theta}$ de equilibrio