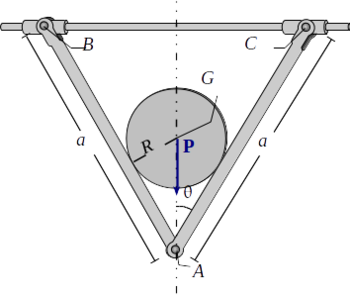
Entrar Página Discusión Historial Go to the site toolbox

Disco apoyado en dos varillas en forma de V

De Laplace

Contenido

1 Enunciado

En el esquema de la figura la barras AB y AC, ambas de longitud a, están articuladas sin rozamiento en A y con sus extremos B y C en un eje horizontal sobre el que pueden deslizar sin rozamiento. El peso de estas barras es despreciable en comparación con el peso P de un disco homogéneo de radio R que se apoya sin rozamiento sobre las barras, manteniéndose todo el sistema en un plano vertical (ver figura). Se pide:

  1. Desvincular el sistema de sólidos y representar los correspondientes "diagramas de sólido libre".
  2. Las reacciones vinculares en B y C para la posición de equilibrio.
  3. La ecuación que determina la posición de equilibrio. ¿Que relación debe existir entre el radio del disco y la longitud de las barras para que el sistema esté en equilibrio en la posición correspondiente a θeq = π / 4?

2 Solución

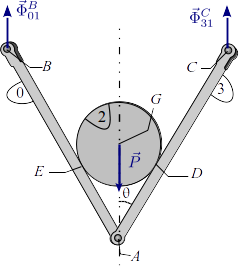
2.1 Diagramas de sólido libre

La figura muestra las fuerzas que actúan sobre cada uno de los sólidos del problema. Como todos los contactos son lisos las fuerzas de reacción son perpendiculares a las superficies de contacto. Hemos añadido una fuerza \vec{N} sobre el sólido "2" que representa el soporte que sostiene a todo el conjunto. Del principio de acción y reacción se deducen las siguientes igualdades entre las fuerzas de reacción vincular

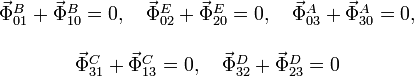
\begin{array}{c} \vec{\Phi}^B_{01}+\vec{\Phi}^B_{10}=0,\quad \vec{\Phi}^E_{02}+\vec{\Phi}^E_{20}=0,\quad \vec{\Phi}^A_{03}+\vec{\Phi}^A_{30}=0,\\ \\ \vec{\Phi}^C_{31}+\vec{\Phi}^C_{13}=0,\quad \vec{\Phi}^D_{32}+\vec{\Phi}^D_{23}=0 \end{array}

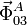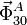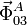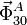Señalemos que no sabemos a priori las direcciones de las fuerzas \vec{\Phi}^A_{03} y \vec{\Phi}^A_{30} , pues no se puede definir una normal en la articulación. Sin embargo, el sistema tiene simetría especular respecto a la línea de puntos indicada. Entonces las fuerzas deben tener esa misma simetría. La única manera de que esto se cumpla es que \vec{\Phi}^A_{03} y \vec{\Phi}^A_{30} sean horizontales.

2.2 Reacciones vinculares en \vec{B} y \vec{C}

La ligadura en B y en C prohíbe los desplazamientos verticales. Las fuerzas de reacción vincular son por tanto verticales, pues al no haber rozamiento no hay componente horizontal. Por la simetría del problema, estas dos fuerzas deben ser iguales, es decir

\vec{\Phi}^B_{01}=\vec{\Phi}^C_{31}

Para encontrar cuanto valen vamos a considerar el sólido conjunto "0+2+3". Las fuerzas externas sobre este sólido son el peso aplicado en el disco y las dos fuerzas de reacción vincular buscadas, como se indica en la figura. La resultante de estas tres fuerzas debe ser nula. Aplicando que \vec{\Phi}^B_{01}=\vec{\Phi}^C_{31} tenemos

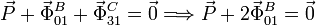
\vec{P}+\vec{\Phi}^B_{01} + \vec{\Phi}^C_{31} = \vec{0} \Longrightarrow \vec{P}+2\vec{\Phi}^B_{01} = \vec{0}

Finalmente tenemos

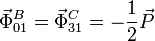
\vec{\Phi}^B_{01} = \vec{\Phi}^C_{31} = -\dfrac{1}{2}\vec{P}

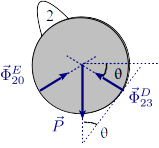
2.3 Ecuación de equilibrio para 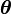\boldsymbol{\theta}

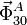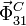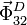Aplicamos la condición de que el momento resultante de las fuerzas que actúan sobre el sólido "3" respecto de cualquier punto debe ser nulo. Escogemos el punto "A" para calcular el momento, pues de este modo nos quitamos de en medio \vec{\Phi}^A_{30}. La fuerza \vec{\Phi}^C_{31} está aplicada en el punto C y la fuerza \vec{\Phi}^D_{32} se aplica en el punto D, el punto de contacto entre el disco y la barra. La distancia entre este punto y la articulación A depende del ángulo θ. De la figura vemos que

\tan\theta = \dfrac{R}{d}

El momento resultante respecto al punto A del sistema de fuerzas actuando sobre la barra es

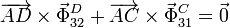
\overrightarrow{AD}\times\vec{\Phi}^D_{32}+\overrightarrow{AC}\times\vec{\Phi}^C_{31}=\vec{0}

De la figura vemos que ambos momentos son perpendiculares al plano y de sentidos opuestos. Así pues, para que el momento total sea nulo los módulos debes ser iguales.

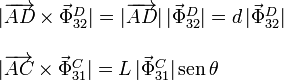
\begin{array}{l} |\overrightarrow{AD}\times\vec{\Phi}^D_{32}| = |\overrightarrow{AD}|\,|\vec{\Phi}^D_{32}| =d\,|\vec{\Phi}^D_{32}| \\ \\ |\overrightarrow{AC}\times\vec{\Phi}^C_{31}|= L\,|\vec{\Phi}^C_{31}| \,\mathrm{sen}\,\theta \end{array}

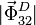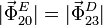En el primer apartado vimos que \vec{\Phi}^C_{31}=-\vec{P}/2. Tenemos que determinar |\vec{\Phi}^D_{32}|. Para ello aplicamos que la suma de fuerzas sobre el sólido "2" debe ser cero. Por simetría |\vec{\Phi}^E_{20}|=|\vec{\Phi}^D_{23}|. Por tanto, para que se anule la componente vertical debe ocurrir que

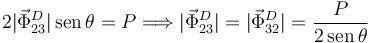
2|\vec{\Phi}^D_{23}|\,\mathrm{sen}\, \theta=P\Longrightarrow |\vec{\Phi}^D_{23}|=|\vec{\Phi}^D_{32}|=\dfrac{P}{2\,\mathrm{sen}\,\theta}

Introduciendo esto en la expresión anterior llegamos a

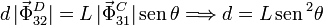
d\,|\vec{\Phi}^D_{32}|= L\,|\vec{\Phi}^C_{31}| \,\mathrm{sen}\,\theta\Longrightarrow d=L\,\mathrm{sen}\,^2\theta

La condición para el valor de equilibrio del ángulo es

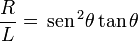
\dfrac{R}{L}=\,\mathrm{sen}\,^2\theta\tan\theta

En el caso θ = π / 4 se obtiene la relación

R = L / 2

2.4 Resolución alternativa

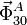Este valor de equilibrio puede calcularse a partir del teorema de las tres fuerzas. Como hemos dicho en el primer apartado, por razones de simetría la fuerza \vec{\Phi}^A_{30} es horizontal. Las rectas soporte de las tres fuerzas que actúan sobre el sólido "3" deben cruzarse en un punto. Observando el dibujo adjunto vemos que

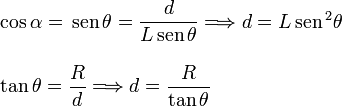
\begin{array}{l} \cos\alpha=\,\mathrm{sen}\,\theta=\dfrac{d}{L\,\mathrm{sen}\,\theta}\Longrightarrow d=L\,\mathrm{sen}\,^2\theta\\ \\ \tan\theta=\dfrac{R}{d}\Longrightarrow d=\dfrac{R}{\tan\theta} \end{array}

Podemos observar que reobtenemos el valor de equilibrio de θ.

Obtenido de "http://tesla.us.es/wiki/index.php/Disco_apoyado_en_dos_varillas_en_forma_de_V"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 20:11, 25 nov 2014. - Esta página ha sido visitada 3.491 veces. - Aviso legal - Acerca de Laplace