Problemas del segundo principio de la termodinámica (GIE)
De Laplace
1 Problemas de boletín
1.1 Cálculo de eficiencias máximas
Calcule el rendimiento máximo que puede tener una máquina térmica que funcione entre
- 0°C y 100°C.
- 100°C y 200°C.
- 27°C y 1200 K.
Halle asimismo el coeficiente de desempeño máximo que pueden tener un refrigerador que funcione entre
- 4°C y 25°C.
- 0°C y 100°C.
Calcule igualmente los valores máximos del coeficiente de desempeño para una bomba de calor que funcione entre las temperaturas de los dos apartados anteriores.
1.2 Asociación de dos máquinas térmicas
Se tiene una máquina de Carnot que opera entre 1500 K y 600 K recibiendo un flujo de calor 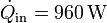 . El calor que sale de ella no se desperdicia sino que se usa para alimentar una segunda máquina de Carnot que opera entre 600 K y 300 K. Halle el rendimiento del conjunto, el calor que sale del sistema y el trabajo total que realiza en la unidad de tiempo.
. El calor que sale de ella no se desperdicia sino que se usa para alimentar una segunda máquina de Carnot que opera entre 600 K y 300 K. Halle el rendimiento del conjunto, el calor que sale del sistema y el trabajo total que realiza en la unidad de tiempo.
Supongamos ahora que en lugar de tratarse de máquinas de Carnot se trata de máquinas reales que tienen un rendimiento del 50% del máximo posible. ¿Cuál sería en ese caso el rendimiento de la asociación, el calor desechado y el trabajo total realizado? ¿Cuánta entropía se produce a lo largo de un ciclo de la máquina?
1.3 Eficiencia de aparatos hipotéticos
Un inventor mantiene que ha desarrollado una máquina térmica que recibe 700 kJ de calor desde un foco térmico a 500 K y produce 300 kJ de trabajo neto transfiriendo el calor sobrante a un foco térmico a 290 K. ¿Es razonable?
Nuestro inventor vuelve a la carga, esta vez con un refrigerador que, asegura, mantiene el contenido refrigerado a 2°C mientras el ambiente se encuentra a 24°C, siendo su potencia de 12000 frigorías (una frigoría equivale a 1 kcal/h de calor extraído) con un consumo de 1000 W. ¿Le hacemos caso?
1.4 Producción de entropía en un ciclo de tres pasos
Para un cilindro que sigue el proceso cíclico descrito en el problema “Sucesión de tres procesos cuasiestáticos”, determine el rendimiento del ciclo relativo al que tendría una máquina de Carnot que operara entre la temperatura máxima y mínima del ciclo.
Halle la producción de entropía en el universo tras la realización del ciclo si se supone que el calor entra desde un foco que está a la máxima temperatura del ciclo y se vierte a un ambiente a la temperatura más baja del ciclo.
1.5 Producción de entropía en los ciclos Otto y Diesel
Para un motor que sigue el ciclo Otto de este problema, calcule el rendimiento relativo al que tendría una máquina reversible que operara entre las temperaturas extremas del ciclo. Halle la producción de entropía al cabo de un ciclo completo, suponiendo que el calor se entrega y absorbe a las temperaturas extremas del ciclo.
Realice también estos cálculos para el ciclo Diesel de este problema
1.6 Producción de entropía en un frigorífico
Un frigorífico doméstico mantiene su interior a 3°C, estando la cocina a 24°C, siendo su un coeficiente de desempeño del 25% respecto al máximo y consumiendo una potencia de 150 W. Determine la cantidad de calor extraído por segundo, el calor arrojado al ambiente y la entropía producida por segundo.
1.7 Calor y entropía en un congelador
Una máquina de fabricar cubitos de hielo produce un cubo de 20 g cada 2 minutos, tomando agua de una conducción a temperatura ambiente de 22°C y produciendo cubitos a −3°C. El COPR de la máquina es de 4.0. Calcule:
- El calor que se debe extraer para fabricar cada cubito. Suponiendo que este calor se extrae a ritmo constante, halle el calor extraído cada segundo.
- El trabajo por segundo (potencia) que debe realizar la máquina para fabricar los cubitos.
- La variación de entropía del agua al convertirse en un cubito de hielo.
- El aumento de entropía del ambiente y del universo en cada segundo.
Datos: Calor específico del agua 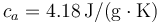 ; Calor específico del hielo
; Calor específico del hielo 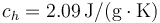 ; Entalpía específica de fusión
; Entalpía específica de fusión 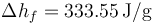 .
.
1.8 Comparación de dos producciones de entropía
Halle la variación de entropía del sistema, del ambiente y del universo en los dos casos siguientes:
- Se vierte un litro de agua a 20°C en una piscina a 80°C.
- Se vierte un litro de agua a 80°C en una piscina a 20°C.
1.9 Cálculo de variaciones de entropía
Calcule la variación de entropía del sistema, del entorno y del universo para los procesos descritos en los problemas
- Mezcla de dos cantidades de agua
- Mezcla de agua e hielo
- Calor necesario para evaporar hielo
- Mezcla de hielo y vapor de agua
1.10 Variación de entropía a volumen y presión constante
Un cilindro de 20 cm de diámetro contiene aire inicialmente a 300 K, siendo la presión externa de 100 kPa. En el cilindro se encuentra un émbolo situado inicialmente a 15 cm de distancia del fondo. Se sumerge el cilindro en un baño térmico a 450 K. Calcule la variación de entropía del gas, del entorno y del universo si:
- El émbolo está atornillado en su posición.
- El émbolo puede deslizarse libremente.
1.11 Variación de entropía por compresión
Considere un prisma vertical de 4 cm de lado que contiene aire. El cilindro contiene un pistón que inicialmente está a 10 cm de altura. La temperatura del gas inicialmente es de 300 K, que también es la temperatura ambiente y la presión exterior es de 100 kPa.
Calcule la variación en la entropía del gas, del entorno y del universo en los cuatro siguientes procesos:
- Se coloca bruscamente una pesa de 4 kg encima del émbolo y las paredes son diatermas.
- Se colocan progresivamente 4 kg de arena, grano a grano y las paredes son diatermas.
- Se coloca bruscamente una pesa de 4 kg encima del émbolo y las paredes son adiabáticas.
- Se colocan progresivamente 4 kg de arena, grano a grano y las paredes son adiabáticas.
1.12 Variación de entropía de dos cámaras de gas
Se tiene un cilindro de 20 cm de diámetro y 60 cm de longitud paredes diatermas en el interior del cual hay dos cámaras de gas. En una hay 4 g de H2 y en la otra 4 g de N2. La temperatura de los dos gases es de 300 K, que también es la temperatura exterior. Separando los dos gases hay un émbolo inicialmente fijado en el centro.
Se libera el pistón y se espera hasta que se vuelva a quedar en equilibrio el sistema. Halle el incremento de entropía de cada gas, del sistema, del entorno y del universo.
Si en vez de liberar el pistón le hacemos un agujero, ¿cuáles son las variaciones de entropía correspondientes?
1.13 Calentamiento ineficiente de una casa
En una casa de la que escapa un flujo de calor de 80000 kJ/h cuando la temperatura exterior es de 15°C y la interior se mantiene constante a 22°C se emplean estufas de resistencia eléctrica. Determine el coeficiente de desempeño relativo al máximo posible, la producción de entropía por hora y el consumo extra respecto a una bomba de calor reversible.
1.14 Producción de entropía por descompresión
Se tiene un cilindro de 20 cm de diámetro tapado por un émbolo situado inicialmente a 14 cm del fondo. En el interior del émbolo se encuentra aire comprimido a 400kPa, siendo la presión exterior 100 kPa. La temperatura exterior y la inicial del aire de la cámara es 294 K. Las paredes del cilindro y el pistón son completamente adiabáticos.
Inicialmente, el pistón está sujeto por un perno, que se libera bruscamente, produciéndose una expansión abrupta.
Calcule la posición final del émbolo, una vez que se alcanza de nuevo el equilibrio, la temperatura final del aire y la variación de entropía en el proceso.
Halle la variación en la exergía del gas en el proceso.
1.15 Producción de entropía en un refrigerador
Para el refrigerador que funciona según un ciclo Otto inverso del problema 3.12, calcule el rendimiento de la segunda ley (comparando el COP con el máximo posible para las temperaturas exterior y de la habitación), así como el trabajo perdido y la producción de entropía del universo en cada ciclo.
1.16 Trabajo máximo en sistema de dos líquidos
Se tienen dos recipientes adiabáticos conteniendo 1.0 kg de agua cada uno, a 27°C y 90°C respectivamente. Se ponen en contacto a través de una pared diaterma. Halle:
- La temperatura final del agua.
- La cantidad de calor transferida.
- La variación de entropía en el proceso.
Suponga ahora que el contacto térmico no se hace directamente sino a través de una máquina térmica reversible que usa los recipientes como foco caliente y foco frío. Teniendo en cuenta que todos los procesos son reversibles
- Halle la temperatura final del agua
- Calcule el calor cedido por el agua caliente y el absorbido por el agua fría
- Determine el trabajo que se puede extraer del sistema.
1.17 Trabajo máximo en sistema de dos gases
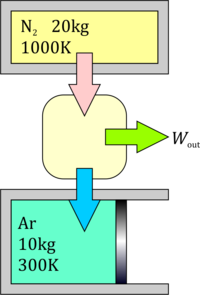
Un tanque de volumen constante contiene 20 kg de nitrógeno a 1000 K y un cilindro a presión constante contiene 10 kg de argón a 300K. Una máquina térmica situada entre el tanque y el cilindro, la cual extrae calor del tanque, realiza un cierto trabajo y expulsa calor al cilindro. Calcule el máximo trabajo que se puede realizar y las temperaturas finales del nitrógeno y el argón en ese caso.
2 Problemas adicionales
2.1 Máquina térmica que alimenta a refrigerador
Un refrigerador que funciona entre una temperatura de -23°C y la temperatura ambiente de 27°C posee un coeficiente de desempeño de 3. Para hacer funcionar este refrigerador se emplea una máquina térmica que funciona entre 327°C y la misma temperatura ambiente, la cual tiene un rendimiento de 0.2. Todo el trabajo producido por la máquina térmica se emplea en hacer funcionar el refrigerador.
- Definimos la eficiencia del conjunto máquina más refrigerador como el calor extraído del foco frío dividido por el calor que es necesario extraer del foco caliente, ¿cuál es la eficiencia del conjunto?
- Si se necesitan extraer 100 J por segundo del foco frío, ¿cuánto calor hay que extraer del foco caliente cada segundo para hacer funcionar el sistema? ¿Cuánto trabajo realiza en un segundo la máquina sobre el refrigerador?
- Calcule la producción de entropía por segundo debida a este conjunto.
- Si tanto el refrigerador como la máquina térmica fueran máquinas de Carnot, ¿cuál sería la eficiencia máxima del conjunto? ¿Qué calor sería necesario sacar del foco caliente en ese caso para extraer 100 J/s del foco frío?
2.2 Aprovechamiento máximo del calor
Se desea caldear una habitación a 22°C cuando la temperatura de la calle es de 5°C. Para ello se dispone de un ladrillo de 50 kg de hierro que previamente se ha calentado a 200°C.
Si se coloca el ladrillo directamente en la habitación, ¿cuánto calor se libera? ¿Cuánta entropía se produce?
Supongamos que en lugar de meter el ladrillo se usa como foco caliente de una máquina reversible que alimenta una bomba de calor también reversible. En ese caso, ¿cuánto calor entra en la habitación? ¿Cuánta entropía se produce?
Dato: Calor específico del hierro 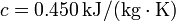
3 Preguntas de test
3.1 Variación de entropía en una expansión
Un gas ideal diatómico contenido en un recipiente ocupa un volumen de 500 cm³ a una presión de 4.0 bares y 300 K de temperatura. Experimenta una expansión hasta un estado final en el que ocupa un volumen de 1000 cm³ a una presión de 1.0 bares. ¿Cuál es la variación de entropía del gas en este proceso?
- A +0.462 J/K
- B −0.693 J/K
- C Depende de cómo ha sido el proceso de expansión.
- D −0.924 J/K
3.2 Falso enunciado del segundo principio
¿Cuál de las siguientes afirmaciones es falsa?
- A No es posible un proceso cuyo único resultado sea la transferencia de calor de un foco frío a uno caliente.
- B En todo proceso real de un sistema su variación de entropía es positiva o nula.
- C El rendimiento de toda máquina térmica es menor o igual al de una máquina térmica reversible que opere entre las temperaturas extremas del ciclo.
- D Es imposible un dispositivo que operando cíclicamente transforme íntegramente calor en trabajo.
3.3 Trabajo perdido en una máquina
Una máquina térmica toma 16000 W de calor de una caldera a 1200 K y expulsa 9600 W a un río a 27°C.
¿Cuánto trabajo se pierde por unidad de tiempo respecto al máximo posible?
- A 5600 W
- B No hay información suficiente para determinarlo.
- C 12000 W
- D 9240 W
Si se consigue reconducir internamente el calor de forma que 8000 W de calor de desecho sean reenviados a la caldera, ¿cuánto vale en ese caso el rendimiento?
- A Tal proceso es imposible.
- B 80%
- C No hay información suficiente para determinarlo.
- D 75%
3.4 Variación de entropía en un proceso adiabático
En un proceso adiabático irreversible ¿aumenta la entropía del sistema? ¿Y la del ambiente?
- A No aumenta ninguna de las dos.
- B Aumentan las dos.
- C Solo la del sistema.
- D Solo la del ambiente.
3.5 Coeficiente de desempeño de un refrigerador
Se usa un refrigerador para mantener líquido una cierta cantidad de nitrógeno a −200°C estando el exterior a 20°C. ¿Cuánto vale el coeficiente de desempeño máximo que puede tener el refrigerador?
- A 3.01
- B 1.33
- C 0.75
- D 0.33
3.6 Calor de desecho y entropía
Una máquina térmica que opera entre 300 K y 1200 K tiene un rendimiento del 50% del máximo posible. Si la máquina desarrolla una potencia de 300 kW, ¿cuánto calor de desecho produce por segundo?
- A 800 kW
- B 300 kW
- C 500 kW
- D 0 kW
¿Cuanta entropía produce la máquina por segundo?
- A +1 (J/K)/s
- B +1000 (J/K)/s
- C 0 (J/K)/s
- D -1000 (J/K)/s
3.7 Posible enunciado del segundo principio
¿Cual de las siguientes afirmaciones es una formulación del segundo principio de la termodinámica?
- A Es imposible un proceso por el cual pase calor de un foco frío a uno caliente.
- B Es imposible un dispositivo que, operando cíclicamente, tenga como único resultado la transformación de trabajo en calor.
- C En todo proceso entre dos estados A y B
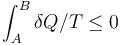
- D Si no entra ni sale energía de un sistema aislado, su entropía solo puede aumentar.
3.8 Variación de entropía en un proceso de un gas
Para el sistema descrito en las preguntas de test T.28, T.29 y T.30 del boletín 2 ¿Cuánto es la variación de entropía del universo en el último proceso?
- A +22.5 mJ/K
- B +17.9 mJ/K
- C 0 mJ/K
- D −22.5 mJ/K
3.9 Enunciado de Kelvin-Planck
¿Cuál de las siguientes procesos está prohibido explícitamente por el enunciado de Kelvin-Planck del segundo principio de la termodinámica?
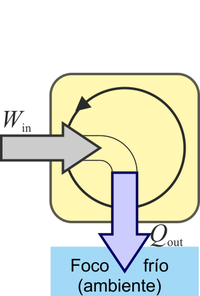
| 
|
| A | B |
|---|---|

| 
|
| C | D |
3.10 Variación de entropía en un proceso
En un proceso efectuado por un sistema entran 90 kJ de calor de un foco a 600 K, salen 30 kJ a un foco a 300 K y el sistema realiza sobre el ambiente un trabajo neto de 80 kJ. ¿Qué podemos asegurar del sistema y el proceso?
- A Que este proceso es imposible.
- B Que la energía interna del sistema aumenta.
- C Que la temperatura del sistema aumenta.
- D Que la energía interna del sistema disminuye.
¿Cuánto varía la entropía del ambiente en este proceso?
- A No existe porque este proceso es imposible.
- B −50 J/K.
- C −150 J/K.
- D +100 J/K
3.11 Posible ciclo de Carnot
¿Cuál de las siguientes curvas corresponde a un ciclo de Carnot en un diagrama TS?

| 
|
| A | B |
|---|---|

| 
|
| C | D |





