Variación de entropía a volumen y presión constante

De Laplace

Contenido

1 Enunciado
2 A volumen constante
3 A presión constante

1 Enunciado

Un cilindro de 20 cm de diámetro contiene aire inicialmente a 300 K, siendo la presión externa de 100 kPa. En el cilindro se encuentra un émbolo situado inicialmente a 15 cm de distancia del fondo. Se sumerge el cilindro en un baño térmico a 450 K. Calcule la variación de entropía del gas, del entorno y del universo si:

El émbolo está atornillado en su posición.
El émbolo puede deslizarse libremente.

2 A volumen constante

En el primer caso tenemos que el calor se le cede al gas, manteniendo éste constante su volumen.

El volumen inicial (y final del gas) vale

$V = \pi r^2 h = \pi\times 0.10^2\times 0.15\,\mathrm{m}^3 = 4.71\times 10^{-3}\,\mathrm{m}^3$

y el número de moles de gas es

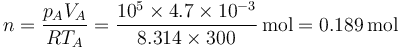
$n = \frac{p_AV_A}{RT_A} = \frac{10^5\times 4.7\times 10^{-3}}{8.314\times 300}\,\mathrm{mol}=0.189\,\mathrm{mol}$

Entropía del gas: Hallamos la variación de la entropía a partir de la fórmula para un gas ideal en función de T y V (para aprovechar que V no cambia)

$\Delta S_\mathrm{sis} = n R\overbrace{\ln\left(\frac{V_B}{V_A}\right)}^{=0}+n c_v\ln\left(\frac{T_B}{T_A}\right)$

Por comportarse el aire como un gas diatómico

$c_v \simeq \frac{5}{2}R = 20.8\,\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}$

lo que da la variación de entropía

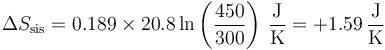
$\Delta S_\mathrm{sis} = 0.189\times 20.8\ln\left(\frac{450}{300}\right)\,\frac{\mathrm{J}}{\mathrm{K}} = +1.59 \,\frac{\mathrm{J}}{\mathrm{K}}$

Entropía del entorno: El entorno cede el calor a temperatura constante (ya que el baño se mantiene en 450 K), por lo que su entropía disminuye en

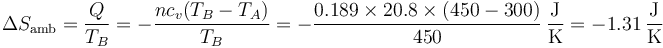
$\Delta S_\mathrm{amb} = \frac{Q}{T_B}=-\frac{nc_v(T_B-T_A)}{T_B} = -\frac{0.189\times 20.8\times(450-300)}{450}\,\frac{\mathrm{J}}{\mathrm{K}}= -1.31\,\frac{\mathrm{J}}{\mathrm{K}}$

Variación total: Sumando las dos contribuciones

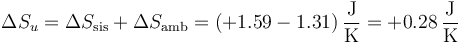
$\Delta S_u = \Delta S_\mathrm{sis} + \Delta S_\mathrm{amb} = (+1.59-1.31)\,\frac{\mathrm{J}}{\mathrm{K}} = +0.28\,\frac{\mathrm{J}}{\mathrm{K}}$

La variación neta es positiva, como corresponde a un proceso posible.

3 A presión constante

En el segundo caso lo que se mantiene constante es la presión del gas, ya que el émbolo puede desplazarse. Hay que señalar que es posible que en el proceso real de calentamiento la presión puede ser variable y producirse una expansión brusca, por ejemplo. Lo que importa es que el estado final es el mismo que habría si se hubiera expandido cuasiestáticamente y por tanto podemos hallar la variación de la entropía suponiendo un proceso cuasiestático con los mismos estados inicial y final

Entropía del gas: Hallamos la variación de la entropía a partir de la fórmula para un gas ideal, ahora en función de T y p

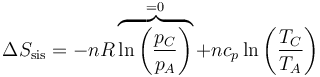
$\Delta S_\mathrm{sis} = -n R\overbrace{\ln\left(\frac{p_C}{p_A}\right)}^{=0}+n c_p\ln\left(\frac{T_C}{T_A}\right)$

Por comportarse el aire como un gas diatómico

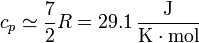
$c_p \simeq \frac{7}{2}R = 29.1\,\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}$

lo que da la variación de entropía

$\Delta S_\mathrm{sis} = 0.189\times 29.1\ln\left(\frac{450}{300}\right)\,\frac{\mathrm{J}}{\mathrm{K}} = +2.23 \,\frac{\mathrm{J}}{\mathrm{K}}$

Esta variación es mayor que en el caso a volumen constante porque ahora aumentan tanto la temperatura como el volumen y los dos factores contribuyen al aumento de entropía.

Entropía del entorno: El entorno cede el calor a temperatura constante (ya que el baño se mantiene en 450 K), por lo que su entropía disminuye en

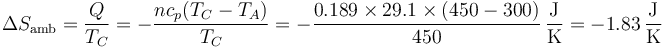
$\Delta S_\mathrm{amb} = \frac{Q}{T_C}=-\frac{nc_p(T_C-T_A)}{T_C} = -\frac{0.189\times 29.1\times(450-300)}{450}\,\frac{\mathrm{J}}{\mathrm{K}}= -1.83\,\frac{\mathrm{J}}{\mathrm{K}}$

También es mayor que en el caso a V cte (y en la misma proporción) ya que se cede más calor al gas.

Variación total: Sumando las dos partes

$\Delta S_u = \Delta S_\mathrm{sis} + \Delta S_\mathrm{amb} = (+2.23-1.83)\,\frac{\mathrm{J}}{\mathrm{K}} = +0.40\,\frac{\mathrm{J}}{\mathrm{K}}$

De nuevo resulta un valor positivo, correspondiente a un proceso posible.

Podemos ver que, en este caso, los dos cálculos son idénticos sin más que cambiar $c v$ por $c p$ . Dado que $c p / c v = 1.4$ ello quiere decir que en el segundo caso el aumento de entropía es un 40% más que en el primero.

Variación de entropía a volumen y presión constante

De Laplace

Contenido

1 Enunciado

2 A volumen constante

3 A presión constante

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES