Preguntas de test del Segundo Principio de la termodinámica (GIE)

De Laplace

1 Variación de entropía en una expansión

Un gas ideal diatómico contenido en un recipiente ocupa un volumen de 500 cm³ a una presión de 4.0 bares y 300 K de temperatura. Experimenta una expansión hasta un estado final en el que ocupa un volumen de 1000 cm³ a una presión de 1.0 bares. ¿Cuál es la variación de entropía del gas en este proceso?

A +0.462 J/K
B −0.693 J/K
C Depende de cómo ha sido el proceso de expansión.
D −0.924 J/K

1.1 Solución

La respuesta correcta es la B.

Conocidos los estados final e inicial, la variación en la entropía, que es una función de estado, puede calcularse sin necesidad de conocer el proceso. En este caso, los datos son el volumen y la temperatura, por lo que podemos usar la expresión

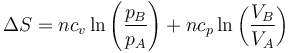
$\Delta S = nc_v\ln\left(\frac{p_B}{p_A}\right)+nc_p\ln\left(\frac{V_B}{V_A}\right)$

El número de moles de gas es

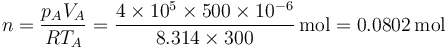
$n = \frac{p_AV_A}{RT_A} = \frac{4\times 10^5\times 500\times 10^{-6}}{8.314\times 300}\,\mathrm{mol}=0.0802\,\mathrm{mol}$

mientras que

$c_v = \frac{5}{2}R = 2.5\times 8.314\,\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}=20.8 \,\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}\qquad\qquad c_p = \frac{7}{2}R = 3.5\times 8.314\,\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}=29.1 \,\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}$

lo que da

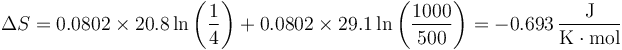
$\Delta S = 0.0802\times 20.8\ln\left(\frac{1}{4}\right)+0.0802\times 29.1\ln\left(\frac{1000}{500}\right) = -0.693\,\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}$

La variación de entropía es negativa ya que lo que disminuye por disminuir la presión es más que lo que aumenta por aumentar el volumen.

2 Falso enunciado del segundo principio

¿Cuál de las siguientes afirmaciones es falsa?

A No es posible un proceso cuyo único resultado sea la transferencia de calor de un foco frío a uno caliente.
B En todo proceso real de un sistema su variación de entropía es positiva o nula.
C El rendimiento de toda máquina térmica es menor o igual al de una máquina térmica reversible que opere entre las temperaturas extremas del ciclo.
D Es imposible un dispositivo que operando cíclicamente transforme íntegramente calor en trabajo.

2.1 Solución

La respuesta correcta es la B.

La respuesta A es verdadera, ya que se trata del enunciado de Clausius del segundo principio. La C también, pues consiste en el Teorema de Carnot. La D es el enunciado de Kelvin-Planck.

La respuesta B parece el principio de aumento de entropía, pero no lo es. Éste habla del aumento de entropía del universo completo, no solo del sistema. En un proceso real la variación de entropía de un sistema puede ser negativa, siempre que la del ambiente sea positiva y más grande.

3 Trabajo perdido en una máquina

Una máquina térmica toma 16000 W de calor de una caldera a 1200 K y expulsa 9600 W a un río a 27°C.

3.1 Pregunta 1

¿Cuánto trabajo se pierde por unidad de tiempo respecto al máximo posible?

A 5600 W
B No hay información suficiente para determinarlo.
C 12000 W
D 9240 W

3.1.1 Solución

La respuesta correcta es la A.

El trabajo perdido se halla como la diferencia entre el que podría haberse realizado y el que realmente se efectúa. Lo mismo se aplica al trabajo perdido por segundo

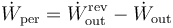
$\dot{W}_\mathrm{per}=\dot{W}^\mathrm{rev}_\mathrm{out}-\dot{W}_\mathrm{out}\,$

Este trabajo puede calcularse a partir del calor de entrada y del de salida como

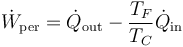
$\dot{W}_\mathrm{per}=\dot{Q}_\mathrm{out}-\frac{T_F}{T_C}\dot{Q}_\mathrm{in}\,$

que en este caso da

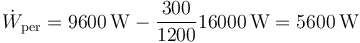
$\dot{W}_\mathrm{per}=9600\,\mathrm{W}-\frac{300}{1200}16000\,\mathrm{W}=5600\,\mathrm{W}$

3.2 Pregunta 2

Si se consigue reconducir internamente el calor de forma que 8000 W de calor de desecho sean reenviados a la caldera, ¿cuánto vale en ese caso el rendimiento?

A Tal proceso es imposible.
B 80%
C No hay información suficiente para determinarlo.
D 75%

3.2.1 Solución

La respuesta correcta es la A.

Este proceso es imposible, ya que supone que el calor iría desde un foco a 300K a uno a 1200K, violando el enunciado de Clausius del segundo principio.

4 Variación de entropía en un proceso adiabático

En un proceso adiabático irreversible ¿aumenta la entropía del sistema? ¿Y la del ambiente?

A No aumenta ninguna de las dos.
B Aumentan las dos.
C Solo la del sistema.
D Solo la del ambiente.

4.1 Solución

La respuesta correcta es la C.

Al ser irreversible, se produce un aumento de entropía del universo. Al ser adiabático, quiere decir que no hay intercambio de calor entre el sistema y el ambiente, por lo que la entropía del ambiente no se ve modificada. Por tanto, todo el aumento de entropía se produce en el interior del sistema.

5 Coeficiente de desempeño de un refrigerador

Se usa un refrigerador para mantener líquido una cierta cantidad de nitrógeno a −200°C estando el exterior a 20°C. ¿Cuánto vale el coeficiente de desempeño máximo que puede tener el refrigerador?

A 3.01
B 1.33
C 0.75
D 0.33

5.1 Solución

La respuesta correcta es la D.

El coeficiente de desempeño máximo es el de un refrigerador reversible, dado por

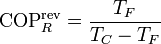
$\mathrm{COP}_R^\mathrm{rev}=\frac{T_F}{T_C-T_F}$

que en este caso vale

$\mathrm{COP}_R^\mathrm{rev}=\frac{73}{293-173}=0.33$

6 Calor de desecho y entropía

Una máquina térmica que opera entre 300 K y 1200 K tiene un rendimiento del 50% del máximo posible. Si la máquina desarrolla una potencia de 300 kW,

6.1 Pregunta 1

¿cuánto calor de desecho produce por segundo?

A 800 kW
B 300 kW
C 500 kW
D 0 kW

6.1.1 Solución

La respuesta correcta es la C.

El rendimiento máximo de una máquina que opere entre estas temperaturas es

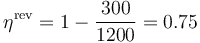
$\eta^\mathrm{rev}=1-\frac{300}{1200}=0.75$

por lo que el de la máquina real vale

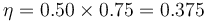
$\eta = 0.50\times 0.75 = 0.375\,$

Si la máquina desrrolla una potencia de 300kW, quiere decir que el flujo de calor de entrada es

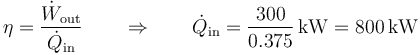
$\eta=\frac{\dot{W}_\mathrm{out}}{\dot{Q}_\mathrm{in}}\qquad\Rightarrow\qquad \dot{Q}_\mathrm{in}=\frac{300}{0.375}\,\mathrm{kW}=800\,\mathrm{kW}$

y, por tanto, el flujo de calor de desecho

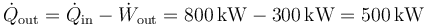
$\dot{Q}_\mathrm{out}=\dot{Q}_\mathrm{in}-\dot{W}_\mathrm{out}=800\,\mathrm{kW}-300\,\mathrm{kW}=500\,\mathrm{kW}$

6.2 Pregunta 2

¿Cuanta entropía produce la máquina por segundo?

A +1 (J/K)/s
B +1000 (J/K)/s
C 0 (J/K)/s
D -1000 (J/K)/s

6.2.1 Solución

La respuesta correcta es la B.

La producción de entropía de la máquina es la combinación de la que disminuye del foco caliente y la que aumenta aen el foco frío.

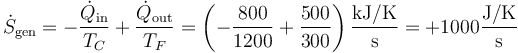
$\dot{S}_\mathrm{gen}=-\frac{\dot{Q}_\mathrm{in}}{T_C}+\frac{\dot{Q}_\mathrm{out}}{T_F}=\left(-\frac{800}{1200}+\frac{500}{300}\right)\frac{\mathrm{kJ}/\mathrm{K}}{\mathrm{s}}=+1000\frac{\mathrm{J}/\mathrm{K}}{\mathrm{s}}$

7 Posible enunciado del segundo principio

¿Cual de las siguientes afirmaciones es una formulación del segundo principio de la termodinámica?

A Es imposible un proceso por el cual pase calor de un foco frío a uno caliente.
B Es imposible un dispositivo que, operando cíclicamente, tenga como único resultado la transformación de trabajo en calor.
C En todo proceso entre dos estados A y B

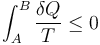
$\int_A^B \frac{\delta Q}{T} \leq 0$

D Si no entra ni sale energía de un sistema aislado, su entropía solo puede aumentar.

7.1 Solución

La respuesta correcta es la D.

La A es falsa porque sí que puede pasar calor de un foco frío a uno caliente, siempre que se realice trabajo (es el principio de los refrigeradores). La B también, pues no hay nada que impida transformar trabajo en calor, es lo que hacen las estufas. La C también, ya que la desigualdad de Clausius es para procesos cíclicos, no para cualquier proceso.

La correcta, por eliminación, es la D, que constituye el principio de aumento de entropía.

8 Variación de entropía en un proceso de un gas

Para el sistema descrito en unas preguntas de test del tema 2 ¿Cuánto es la variación de entropía del universo en el último proceso?

A +22.5 mJ/K
B +17.9 mJ/K
C 0 mJ/K
D −22.5 mJ/K

8.1 Solución

La respuesta correcta es la C.

El proceso de compresión es isotermo y cuasiestático. En este proceso, al comprimirse el volumen se realiza trabajo sobre el gas, liberándose una cantidad equivalente de calor (puesto que la energía interna no cambia). Por tanto la variación de entropía del sistema es negativa

$\Delta S_\mathrm{sis}=-\frac{|\mathrm{Q}|}{T}$

y la del ambiente es positiva, ya que el calor que sale del sistema va a parar al ambiente, el cual está a la misma temperatura

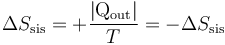
$\Delta S_\mathrm{sis}=+\frac{|\mathrm{Q}_\mathrm{out}|}{T}=-\Delta S_\mathrm{sis}$

siendo la variación de entropía del universo

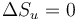
$\Delta S_u = 0\,$

Este proceso es reversible. Comprimimos el gas aumentando lentamente la presión, pero si reducimos esta infinitesimalmente el aire empezará a expandirse, dándose la vuelta al proceso.

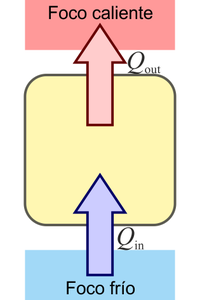
9 Enunciado de Kelvin-Planck

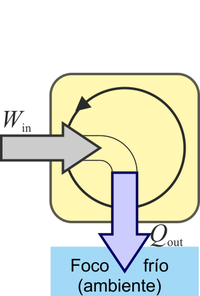
¿Cuál de las siguientes procesos está prohibido explícitamente por el enunciado de Kelvin-Planck del segundo principio de la termodinámica?

A	B


C	D

9.1 Solución

La respuesta correcta es la B.

El enunciado de Kelvin-Planck es:

Es imposible construir una máquina que, operando en un ciclo, produzca como único efecto la extracción de calor de un foco y la realización de una cantidad equivalente de trabajo

Puesto que el enunciado de Clausius es equivalente al de Kelvin-Planck, éste también prohíbe el caso D, pero no lo hace explícitamente.

es decir, que lo que prohíbe es que se absorba calor de un foco (el llamarlo frío o caliente es irrelevante, pues solo hay uno) y ese calor se transforme en trabajo.

10 Variación de entropía en un proceso

En un proceso efectuado por un sistema entran 90 kJ de calor de un foco a 600 K, salen 30 kJ a un foco a 300 K y el sistema realiza sobre el ambiente un trabajo neto de 80 kJ.

10.1 Pregunta 1

¿Qué podemos asegurar del sistema y el proceso?

A Que este proceso es imposible.
B Que la energía interna del sistema aumenta.
C Que la temperatura del sistema aumenta.
D Que la energía interna del sistema disminuye.

10.1.1 Solución

La respuesta correcta es la D.

El proceso no es imposible, ya que al no tratarse de un proceso cíclico no hay necesidad de que el trabajo iguale a la diferencia entre el calor que entra y el que sale. El primer principio de la termodinámica nos dice

$\Delta U = Q_\mathrm{in}-Q_\mathrm{out}+W_\mathrm{in}-W_\mathrm{out}=90\,\mathrm{kJ}-30\,\mathrm{kJ}+0-80\,\mathrm{kJ}=-20\,\mathrm{kJ}$

Por tanto la energía interna del sistema disminuye.

10.2 Pregunta 2

¿Cuánto varía la entropía del ambiente en este proceso?

A No existe porque este proceso es imposible.
B −50 J/K.
C −150 J/K.
D +100 J/K

10.2.1 Solución

La respuesta correcta es la B.

La variación de entropía del ambiente se compone de una disminución en el foco caliente y de un incremento en el foco frío

$\Delta S_\mathrm{amb}=-\frac{90\,\mathrm{kJ}}{600\,\mathrm{K}}+\frac{30\,\mathrm{kJ}}{300\,\mathrm{K}} = -50\,\frac{\mathrm{J}}{\mathrm{K}}$

11 Posible ciclo de Carnot

¿Cuál de las siguientes curvas corresponde a un ciclo de Carnot en un diagrama TS?

A	B


C	D

11.1 Solución

La respuesta correcta es la D.

Un ciclo de Carnot está formado por dos isotermas y dos adiabáticas. En un diagrama TS una isoterma es una recta horizontal. Un proceso adiabático reversible es un proceso isentrópico, por lo que su gráfica es una línea vertical. Por tanto el ciclo de Carnot, como se ha estudiado en el curso, es un rectángulo.

Preguntas de test del Segundo Principio de la termodinámica (GIE)

De Laplace

Contenido

1 Variación de entropía en una expansión

1.1 Solución

2 Falso enunciado del segundo principio

2.1 Solución

3 Trabajo perdido en una máquina

3.1 Pregunta 1

3.1.1 Solución

3.2 Pregunta 2

3.2.1 Solución

4 Variación de entropía en un proceso adiabático

4.1 Solución

5 Coeficiente de desempeño de un refrigerador

5.1 Solución

6 Calor de desecho y entropía

6.1 Pregunta 1

6.1.1 Solución

6.2 Pregunta 2

6.2.1 Solución

7 Posible enunciado del segundo principio

7.1 Solución

8 Variación de entropía en un proceso de un gas

8.1 Solución

9 Enunciado de Kelvin-Planck

9.1 Solución

10 Variación de entropía en un proceso

10.1 Pregunta 1

10.1.1 Solución

10.2 Pregunta 2

10.2.1 Solución

11 Posible ciclo de Carnot

11.1 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES