Entrar Página Discusión Historial Go to the site toolbox

Calor y entropía en un congelador

De Laplace

Contenido

1 Enunciado

Una máquina de fabricar cubitos de hielo produce un cubo de 20 g cada 2 minutos, tomando agua de una conducción a temperatura ambiente de 22°C y produciendo cubitos a −3°C. El COPR de la máquina es de 4.0. Calcule:

  1. El calor que se debe extraer para fabricar cada cubito. Suponiendo que este calor se extrae a ritmo constante, halle el calor extraído cada segundo.
  2. El trabajo por segundo (potencia) que debe realizar la máquina para fabricar los cubitos.
  3. La variación de entropía del agua al convertirse en un cubito de hielo.
  4. El aumento de entropía del ambiente y del universo en cada segundo.

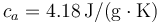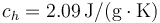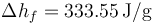Datos: Calor específico del agua c_a=4.18\,\mathrm{J}/(\mathrm{g}\cdot\mathrm{K}); Calor específico del hielo c_h=2.09\,\mathrm{J}/(\mathrm{g}\cdot\mathrm{K}); Entalpía específica de fusión \Delta h_f = 333.55\,\mathrm{J}/\mathrm{g}.

2 Calor extraído

El calor que se extrae del agua y entra en el refrigerador se compone de tres contribuciones

  • El calor que hay que extraer para llevar el agua a 0°C
Q_1 = m c_a\,\Delta T = 20\,\mathrm{g}\times 4.18\frac{\mathrm{J}}{\mathrm{g}\cdot\mathrm{K}}(273-295)\mathrm{K} = -1840\,\mathrm{J}
  • El calor que hay que extraer para congelar el agua
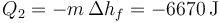
Q_2 = -m\,\Delta h_f = -6670\,\mathrm{J}
Este calor es negativo, pues se saca del agua. Si fuera positivo querría decir que si calentamos agua obtenemos hielo.
  • El calor que hay que extraer para llevar el hielo a −3°C
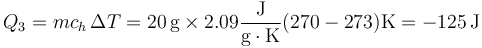
Q_3 = m c_h\,\Delta T = 20\,\mathrm{g}\times 2.09\frac{\mathrm{J}}{\mathrm{g}\cdot\mathrm{K}}(270-273)\mathrm{K} = -125\,\mathrm{J}

El calor total que hay que extraer para fabricar cada cubito es

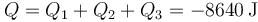
Q=Q_1+Q_2+Q_3 = -8640\,\mathrm{J}

Desde el punto de vista del refrigerador, este es un calor que entra en él, por lo que será

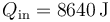
Q_\mathrm{in}=8640\,\mathrm{J}

Este calor se extrae cada 2 minutos. El calor extraído por segundo es

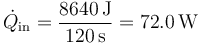
\dot{Q}_\mathrm{in}=\frac{8640\,\mathrm{J}}{120\,\mathrm{s}}=72.0\,\mathrm{W}

3 Potencia necesaria

El coeficiente de desempeño de un refrigerador, COPR, se define como

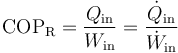
\mathrm{COP}_\mathrm{R}=\frac{Q_\mathrm{in}}{W_\mathrm{in}}=\frac{\dot{Q}_\mathrm{in}}{\dot{W}_\mathrm{in}}

por lo que despejando

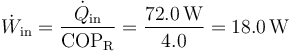
\dot{W}_\mathrm{in}=\frac{\dot{Q}_\mathrm{in}}{\mathrm{COP}_\mathrm{R}}=\frac{72.0\,\mathrm{W}}{4.0}=18.0\,\mathrm{W}

4 Variación de entropía del agua

Como en el caso del calor, tenemos tres variaciones de entropía, todas ellas negativas.

\Delta S_1 = \int_{T_i}^{T_f}\frac{\delta Q}{T}=mc_a\int_{T_i}^{T_f}\frac{\mathrm{d}T}{T}=mc_a\ln\left(\frac{T_f}{T_i}\right)
que para este caso da
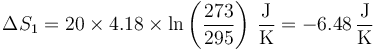
\Delta S_1 = 20\times 4.18\times\ln\left(\frac{273}{295}\right)\,\frac{\mathrm{J}}{\mathrm{K}} = -6.48\,\frac{\mathrm{J}}{\mathrm{K}}
  • Variación en la congelación. Este proceso es isotermo, por lo que
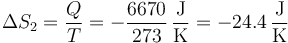
\Delta S_2 = \frac{Q}{T}=-\frac{6670}{273}\,\frac{\mathrm{J}}{\mathrm{K}}=-24.4\,\frac{\mathrm{J}}{\mathrm{K}}
  • Variación en el enfriamiento del hielo. Como en el primer caso
\Delta S_3 = 20\times 2.09\times\ln\left(\frac{270}{273}\right)\,\frac{\mathrm{J}}{\mathrm{K}} = -0.46\,\frac{\mathrm{J}}{\mathrm{K}}

Sumando las tres contribuciones

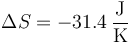
\Delta S = -31.4\,\frac{\mathrm{J}}{\mathrm{K}}

La entropía del agua disminuye porque está enfriándose. No hay ninguna imposibilidad en esto ya que no se trata de un sistema aislado. Habrá que calcular la variación de entropía de todo el universo para estudiar su posibilidad.

5 Variación total de entropía

En el cálculo de la entropía total hay que tener mucho cuidado a qué llamamos sistema y a qué llamamos ambiente. El resultado total debe ser el mismo, pero los términos por separado pueden variar

5.1 El sistema es el agua

Si consideramos que el agua es nuestro sistema y el refrigerador y todo lo demás es el ambiente, entonces, la variación de entropía del sistema es la que ya hemos calculado,

\Delta S_\mathrm{sis} = -31.4\,\frac{\mathrm{J}}{\mathrm{K}}

mientras que la del ambiente se debe a que arrojamos al ambiente un calor

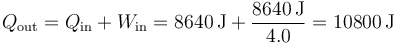
Q_\mathrm{out}=Q_\mathrm{in}+W_\mathrm{in}=8640\,\mathrm{J}+\frac{8640\,\mathrm{J}}{4.0} = 10800\,\mathrm{J}

siendo la temperatura ambiente 22°C. Por tanto la variación de entropía del ambiente es

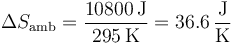
\Delta S_\mathrm{amb}=\frac{10800\,\mathrm{J}}{295\,\mathrm{K}} = 36.6\,\frac{\mathrm{J}}{\mathrm{K}}

La variación de entropía del universo es la suma de estas dos

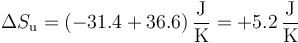
\Delta S_\mathrm{u}=(-31.4+36.6)\,\frac{\mathrm{J}}{\mathrm{K}}=+5.2\,\frac{\mathrm{J}}{\mathrm{K}}

que es positiva, como corresponde a un proceso posible.

Esa es la producción de entropía por cada cubito, en 120 segundos. La producción de entropía por segundo es

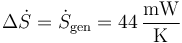
\Delta \dot{S}=\dot{S}_\mathrm{gen}=44\,\frac{\mathrm{mW}}{\mathrm{K}}

5.2 El sistema es el refrigerador

Si consideramos que nuestro sistema es el refrigerador, entonces, dado que éste opera en un proceso cíclico

ΔSsis = 0

y la variación de entropía es toda debida al ambiente (que ahora incluye el agua). La máquina quita entropía de un lado y la arroja en otro (en exceso, ya que se produce entropía). Aquí existe la tentación de usar la fórmula para una máquina que opera entre dos focos térmicos

\Delta S_u=\Delta S_\mathrm{amb} = -\frac{Q_\mathrm{in}}{T_f}+\frac{Q_\mathrm{out}}{T_c}        (NO APLICABLE)

Sin embargo, esta fórmula no se puede aplicar aquí, ya que la temperatura del foco frío no es siempre la misma, ya que el agua se va enfriando. Habría que considerar variaciones diferenciales y escribir

\Delta S_u = -\int\frac{\delta Q_\mathrm{in}}{T_f}+\frac{Q_\mathrm{out}}{T_c}

El cálculo del primer término es exactamente el mismo que ya hemos hecho para hallar la variación de entropía del agua, mientras que el segundo es igual a como lo hemos calculado en el apartado anterior, por lo que

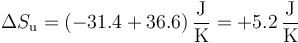
\Delta S_\mathrm{u}=(-31.4+36.6)\,\frac{\mathrm{J}}{\mathrm{K}}=+5.2\,\frac{\mathrm{J}}{\mathrm{K}}

y por segundo

\Delta \dot{S}=\dot{S}_\mathrm{gen}=44\,\frac{\mathrm{mW}}{\mathrm{K}}
Obtenido de "http://tesla.us.es/wiki/index.php/Calor_y_entrop%C3%ADa_en_un_congelador"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 21:11, 16 sep 2013. - Esta página ha sido visitada 16.897 veces. - Aviso legal - Acerca de Laplace