De Laplace

Contenido

1 Problemas de boletín
2 Problemas adicionales
3 Preguntas de test

1 Problemas de boletín

1.1 Ejemplo de máquina térmica

Una máquina térmica consume 240 kg de carbón por hora, siendo el poder calorífico de este combustible de 13.0×10³ kcal/kg. Si la máquina tiene un rendimiento del 25% calcule el trabajo suministrado por la máquina y el calor cedido al foco frío en una hora

1.2 Rendimiento de un ciclo de tres pasos

Para un cilindro que sigue el proceso cíclico descrito en el problema “sucesión de tres procesos cuasiestáticos”, determine el rendimiento del ciclo considerado como una máquina térmica.

1.3 Rendimiento de una máquina térmica real

Una máquina térmica que funciona entre 200°C y 80.0°C alcanza un 20.0% de su rendimiento teórico máximo. ¿Cuanta energía debe absorber para realizar 10.0 kJ de trabajo?

1.4 Ejemplo de frigorífico de Carnot

Una máquina frigorífica de las que se emplean para fabricar hielo funciona segín un ciclo de Carnot reversible absorbiendo calor de un tanque de agua a 0.00°C y cediéndolo al aire en el interior de un local que se mantiene a 26.0°C. La máquina fabrica 223 kg de hielo en un día. Calcule el trabajo consumido y el calor cedido al aire.

1.5 Rendimiento de un aparato de aire acondicionado

Para refrescar una habitación se emplea un aparato de aire acondicionado con un coeficiente de desempeño (COP) de 4. El exterior se encuentra a 34°C mientras que el interior del despacho se mantiene a 24°C. El despacho, que esta vacío, tiene una ventana de vidrio por la cual entra calor desde el exterior. Si el calor que entra por la ventana en la unidad de tiempo es 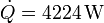$\dot{Q}=4224\,\mathrm{W}$ , calcule el trabajo por segundo (potencia) que debe realizar el aparato para mantener la temperatura interior y la cantidad de calor que es arrojada al exterior.

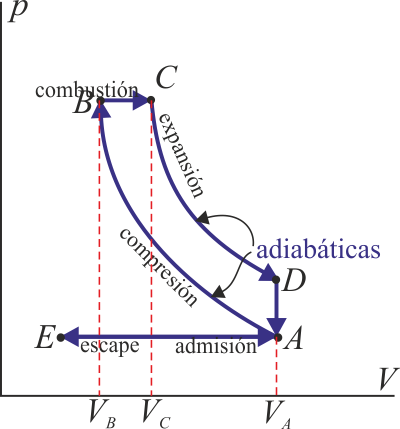
1.6 Eficiencia de un ciclo Otto

Un ciclo Otto ideal modela el comportamiento de un motor de explosión. Este ciclo está formado por seis pasos, según se indica en la figura. Pruebe que el rendimiento de este ciclo viene dado por la expresión

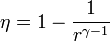
$\eta = 1-\frac{1}{r^{\gamma-1}}$

siendo $r = V A / V B$ la razón de compresión igual al cociente entre el volumen al inicio del ciclo de compresión y al final de él. Para ello, halle el rendimiento a partir del calor que entra en el sistema y el que sale de él; exprese el resultado en términos de las temperaturas en los vértices del ciclo y, con ayuda de la ley de Poisson, relacione este resultado con los volúmenes $V A$ y $V B$ .

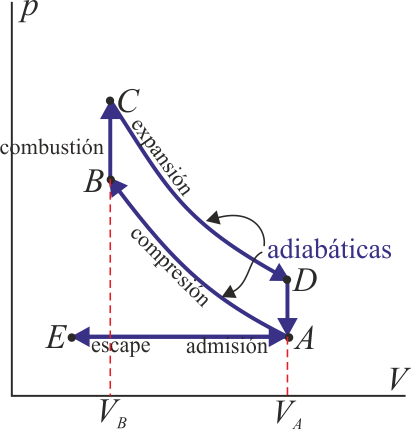
1.7 Caso práctico de ciclo Otto

Suponga un motor de gasolina de 1400 cm³ de cilindrada que se puede modelar mediante un ciclo Otto ideal con una relación de compresión de 8. Al inicio de la fase de compresión, el aire está a 100 kPa y 17°C. En la combustión se añaden 800 kJ/kg de calor. Determine la temperatura y la presión máximas que se producen en el ciclo, la salida de trabajo neto y el rendimiento de este motor.

Si este motor trabaja a 3000rpm, ¿cuánto es la potencia generada?

1.8 Eficiencia de un ciclo Diesel

Un motor diésel puede modelarse con el ciclo ideal formado por seis pasos reversibles, según se indica en la figura. Pruebe que el rendimiento de este ciclo viene dado por la expresión

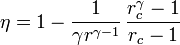
$\eta = 1 -\frac{1}{\gamma r^{\gamma-1}}\,\frac{r_c^\gamma-1}{r_c-1}$

siendo $r = V A / V B$ la razón de compresión y $r c = V C / V B$ la relación de combustión. El método para obtener este resultado es análogo al empleado para el ciclo Otto. Compare los rendimientos del ciclo Otto y el Diesel. ¿Cuáles son las ventajas e inconvenientes respectivos?

1.9 Caso práctico de ciclo Diesel

Suponga un motor diésel turbo con una cilindrada de 1700 cm³. En este motor el aire a la entrada está a una presión de 150 kPa y una temperatura de 17 °C. Si para este motor la razón de compresión es 18 y la de combustión vale 2, determine los volúmenes, presiones y temperaturas de cada vértice del ciclo, así como su rendimiento y el calor y el trabajo intercambiados por el motor.

1.10 Eficiencia de un ciclo Brayton

Un ciclo Brayton (o Joule) ideal modela el comportamiento de una turbina, como las empleadas en las aeronaves. Este ciclo está formado por cuatro pasos reversibles, según se indica en la figura. Pruebe que el rendimiento de este ciclo viene dado por la expresión

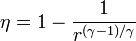
$\eta = 1-\frac{1}{r^{(\gamma-1)/\gamma}}$

siendo $r = p B / p A$ la relación de presión igual al cociente entre la presión al final del proceso de compresión y al inicio de él. El método para obtener este resultado es análogo al empleado para el ciclo Otto.

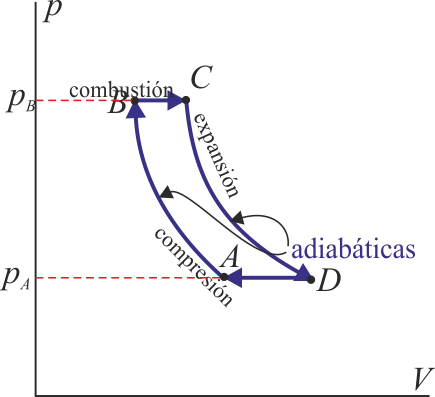
1.11 Caso práctico de ciclo Brayton

Una central eléctrica de turbina de gas que opera en un ciclo Brayton ideal tiene una relación de presión de 8. La temperatura del gas es de 300 K en la entrada del compresor y de 1300 K en la entrada de la turbina. Determine la temperatura del gas a la salida del compresor y de la turbina, y la eficiencia de esta turbina.

1.12 Ejemplo de bomba de calor de Carnot

Una bomba de calor se emplea para mantener caliente una vivienda que se encuentra a 20.0°C siendo la temperatura exterior -5.00°C. Suponiendo que la bomba de calor es una máquina de Carnot invertida, calcule cuantos julios de energía procedentes del medio ambiente exterior serán transferidos al interior de la vivienda por cada julio de energía eléctrica consumida. Explique las ventajas e inconvenientes de este sistema de calefacción frente a uno convencional de disipación de energía en una resistencia eléctrica.

1.13 Refrigerador que sigue un ciclo Otto

Se desea construir un refrigerador que funcione con un ciclo Otto inverso. Para ello se tiene una habitación cuya temperatura se desea mantener en 250K, estando el ambiente exterior a 300K y a una presión de 100kPa.

En una de las paredes de la habitación se instala la unidad refrigeradora, que experimenta el siguiente ciclo:

Inicialmente (estado A) una cámara de 0.1m³ está llena de aire (supuesto gas ideal) a la presión y temperatura exteriores, y aislada térmicamente del interior.

A→B: La cámara se aísla del exterior y se expande rápidamente hasta un volumen de 0.2m³. Esta expansión se puede modelar como un proceso adiabático cuasiestático.

B→C: Manteniendo el volumen fijo, se deja que intercambie calor con la habitación, hasta que la temperatura del aire de la cámara iguale a la de la habitación.

C→D: La cámara se comprime rápidamente hasta volver a un volumen de 0.1m³. Esta compresión también se puede modelar como un proceso adiabático cuasiestático.

D→A: Manteniendo el volumen fijo, se deja ahora que intercambie calor con el exterior, hasta que la temperatura del aire de la cámara iguale a la exterior.

Para este proceso cíclico:

Represente de forma esquemática el ciclo en un diagrama pV.
Calcule la presión, volumen y temperatura del gas en cada uno de los vértices del ciclo.
Calcule el calor intercambiado por el aire con la habitación y con el exterior.
Determine el coeficiente de desempeño COP_R de este refrigerador.
Calcule la proporción entre este coeficiente de desempeño y el máximo que podría alcanzar un refrigerador que operara entre las temperaturas indicadas.

Datos: Constante de los gases ideales: 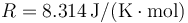$R=8.314\,\mathrm{J}/(\mathrm{K}\cdot\mathrm{mol})$ , Relación entre capacidades caloríficas del aire γ = 1.4.

2 Problemas adicionales

2.1 Consumo de un coche de gasolina

Un Seat León TSI 2.0 amarillo posee una potencia de 210 CV y una relación de compresión de 9.6.

¿Cuánto calor hace falta producir por segundo para circular a la máxima potencia?
¿Cuánta gasolina consumiría a los 100 km, recorridos a máxima potencia a 160 km/h?

Datos: 1 CV = 0.736 kW; Rendimiento de un ciclo Otto ideal: $η = 1 - 1 / r γ - 1$ ; Calor generado en la combustión de 1 litro de gasolina: 33000 kJ.

2.2 Sobrecoste originado por la luz de un frigorífico

El interruptor de la luz interior de un frigorífico está estropeado, de modo que la luz está siempre encendida. La luz interior consume una potencia de 40.0 W. Si la eficiencia del frigorífico es 1.3, y el coste de la electricidad es de 14.2 céntimos por kWh, calcule el incremento en el consumo del frigorífico y el coste añadido por año si no se arregla el interruptor.

2.3 Caso de ciclo Ericsson

Se tiene un cilindro vertical de paredes no aislantes, en cuyo interior se encuentra aire (considerado como un gas ideal diatómico). El cilindro tiene sección cuadrada de lado 4 cm y está cerrado por un pistón horizontal que puede deslizarse sin rozamiento.

Inicialmente el pistón se encuentra a una altura de 10 cm y el aire está en equilibrio térmico y mecánico con el exterior a una temperatura de 300 K y una presión 100 kPa.

Se procede entonces a efectuar el siguiente ciclo

A→B El gas se comprime lentamente, colocando sobre la tapa el equivalente a 4 kg de arena, sin que se modifique la temperatura exterior.

B→C Sin retirar la arena, se calienta lentamente el gas, hasta que el volumen vuelve a ser el inicial.

C→D Manteniendo constante la nueva temperatura, se van retirando los granos de arena hasta que no queda ni uno.

D→A Se enfría gradualmente el gas, hasta que su volumen vuelve a ser el inicial.

A la vista de este ciclo:

Represente gráficamente el ciclo en un diagrama pV.
Para cada uno de los pasos, halle (tomando $g=10\,\mathrm{m}/\mathrm{s}^2$ )

El trabajo y el calor que se intercambian, indicando si cada uno entra en el sistema o sale de él.
La variación de la energía interna y de la entalpía del gas en cada paso.

Calcule el trabajo neto que desarrolla el sistema sobre el entorno.
Halle el calor total absorbido por el gas (sin descontar el que cede al entorno).
Calcule el rendimiento del ciclo, definido como:

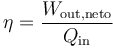
$\eta = \frac{W_{\mathrm{out},\mathrm{neto}}}{Q_\mathrm{in}}$

2.4 Ciclo de Stirling

Un Ciclo de Stirling ideal, sin regeneración, está formado por los siguientes pasos:

Inicialmente tenemos 500 cm³ de aire a 300 K y 100 kPa (estado A)

A→B Se comprime el gas de forma isoterma, hasta que se reduce su volumen a 50 cm³

B→C Se calienta el gas hasta una temperatura de 450 K, manteniendo fijado su volumen.

C→D Se expande el gas a temperatura constante hasta que vuelve a su volumen inicial.

D→A Se enfría el gas manteniendo constante su volumen hasta que su temperatura vuelve a ser la inicial

Para este ciclo.

Indique gráficamente como sería en un diagrama pV.
Calcule el trabajo y el calor que entran en el sistema en cada uno de los cuatro pasos.
Calcule el rendimiento del ciclo.

En un ciclo de Stirling con regeneración, el calor liberado en el proceso D\→A no se pierde sino que se emplea para efectuar el calentamiento en B→C

Calcule el rendimiento del ciclo de Stirling con regeneración. ¿Es mayor o menor que el de una máquina de Carnot que opere entre las mismas temperaturas?

2.5 Refrigeración de una habitación

En una habitación de 15 m×10 m×3 m hay aire (equivalente a un gas ideal diatómico de peso molecular 28.97 g/mol) a 40 °C (que también es la temperatura exterior) y 100 kPa.

¿Cuál es la masa de aire contenida en la habitación?
Con un aparato de aire acondicionado se baja la temperatura de la habitación (con las ventanas y puertas cerradas) hasta 22 °C. ¿Cuánto calor sale de la habitación?
¿Cuánto varía la entropía del aire de la habitación en el proceso anterior?
¿Cuánto es el coeficiente de desempeño (COP_R) máximo que puede tener un aparato de aire acondicionado que funcione entre las dos temperaturas indicadas?
Si el COP_R del aparato empleado es 3.0, ¿cuánto calor de desecho se expulsa al exterior?

2.6 Consumo de un refrigerador

Se tiene un congelador en forma de cubo de 60 cm×60 cm×60 cm cuyas paredes son de fibra de vidrio de 4 cm de grosor. La temperatura interior del congelador es −3 °C y la exterior es de +22 °C

¿Cuánto vale aproximadamente el calor que entra en el congelador por segundo?
¿Cuál es el trabajo por segundo mínimo necesario para hacer funcionar este congelador y mantener constante la temperatura interior?
Suponga que la potencia real necesaria para hacerlo funcionar es de 123 W. ¿Cuánto es la producción de entropía por segundo en el universo debida a este refrigerador?
Suponga que se introduce en el congelador una cubitera con 200 g de agua a temperatura ambiente. ¿Cuánto trabajo debe introducirse en el congelador para fabricar los cubitos?

Datos: Conductividad térmica de la fibra de vidrio: 0.04 W/(m·K); Calor específico del agua: 4.18 kJ/(kg·K); Calor específico del hielo: 2.09 kJ/(kg·K); Entalpía específica de fusión del agua: 334 kJ/kg.

2.7 Bomba de calor alimentada por máquina térmica

Se desea mantener constante la temperatura de un recinto en 27 °C, siendo la temperatura exterior de −3 °C. El flujo de calor que escapa al exterior es de 5400 W.

¿Cuánto vale la resistencia térmica de las paredes?
Si para mantener la temperatura del recinto se emplea una bomba de calor reversible, ¿cuánto trabajo debe absorber la bomba por segundo?
Para obtener este trabajo se emplea una máquina térmica, también reversible, que opera entre 1350 K y la temperatura exterior. ¿Cuánto calor toma del foco caliente por segundo y cuánto expulsa al foco frío?
Para este conjunto de habitación, bomba y máquina, ¿cuánto vale la producción de entropía por segundo en cada uno de los tres elementos y en conjunto?
Suponga ahora que tanto la bomba de calor como la máquina tienen una eficiencia del 50% respecto a las reversibles. ¿Cuáles son en ese caso las respuestas a las preguntas de los apartados 2, 3 y 4?

3 Preguntas de test

3.1 Rendimiento de una máquina térmica

Una máquina térmica toma 16000 W de calor de una caldera a 1200 K y expulsa 9600 W a un río a 27°C. ¿Cuánto vale el rendimiento de la máquina?

A 40%
B 75%
C 60%
D No hay información suficiente para determinarlo.

3.2 Gráfica de un ciclo Diesel

¿Cuál de las siguientes figuras corresponde a un ciclo Diesel en un diagrama pV?

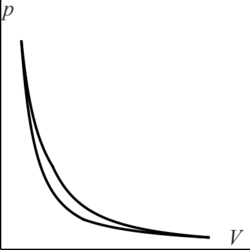
A	B


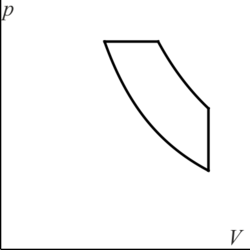
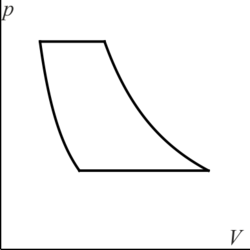
C	D

3.3 Propiedades de un proceso cíclico

Un sistema termodinámico experimenta un proceso cíclico. En este proceso…

A El calor neto que entra en el sistema es nulo.
B El incremento de energía interna es nulo.
C El trabajo neto realizado sobre el sistema es nulo.
D Las otras tres afirmaciones son ciertas.

3.4 Descripción de un ciclo de Carnot

Un ciclo de Carnot ideal está formado por…

A Dos adiabáticas y dos isócoras.
B Dos isotermas y dos adiabáticas.
C Dos isotermas y dos isócoras.
D Dos adiabáticas, una isócora y una isóbara.

3.5 Procesos de una máquina de vapor

¿En qué parte del ciclo simplificado de una máquina de vapor entra un trabajo positivo en el sistema?

A En el condensador
B En la bomba o compresor.
C En la caldera.
D En la turbina.

3.6 Consumo de un coche de gasolina