Ciclo Brayton (GIE)

De Laplace

Contenido

1 Enunciado
2 Descripción del ciclo
3 Eficiencia en función del calor
4 Eficiencia en función de las temperaturas
5 Eficiencia en función de la relación de presión
6 Caso práctico
- 6.1 Eficiencia
- 6.2 Temperaturas
7 Motores de reacción
8 Enlaces

1 Enunciado

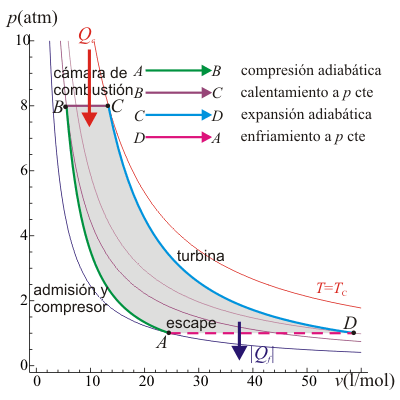
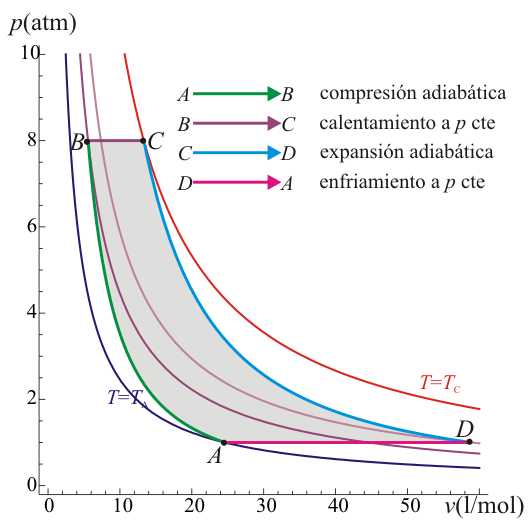
Un ciclo Brayton (o Joule) ideal modela el comportamiento de una turbina, como las empleadas en las aeronaves. Este ciclo está formado por cuatro pasos reversibles, según se indica en la figura. Pruebe que el rendimiento de este ciclo viene dado por la expresión

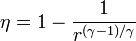
$\eta = 1-\frac{1}{r^{(\gamma-1)/\gamma}}$

siendo $r = p B / p A$ la relación de presión igual al cociente entre la presión al final del proceso de compresión y al inicio de él. El método para obtener este resultado es análogo al empleado para el ciclo Otto.

2 Descripción del ciclo

El ciclo Brayton describe el comportamiento ideal de un motor de turbina de gas, como los utilizados en las aeronaves. Las etapas del proceso son las siguientes:

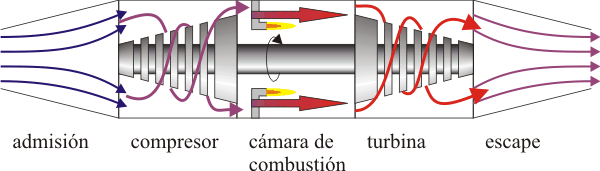
Admisión: El aire frío y a presión atmosférica entra por la boca de la turbina
Compresor: El aire es comprimido y dirigido hacia la cámara de combustión mediante un compresor (movido por la turbina). Puesto que esta fase es muy rápida, se modela mediante una compresión adiabática A→B.
Cámara de combustión: En la cámara, el aire es calentado por la combustión del queroseno. Puesto que la cámara está abierta el aire puede expandirse, por lo que el calentamiento se modela como un proceso isóbaro B→C.
Turbina: El aire caliente pasa por la turbina, a la cual mueve. En este paso el aire se expande y se enfría rápidamente, lo que se describe mediante una expansión adiabática C →D.
Escape: Por último, el aire enfriado (pero a una temperatura mayor que la inicial) sale al exterior. Técnicamente, este es un ciclo abierto ya que el aire que escapa no es el mismo que entra por la boca de la turbina, pero dado que sí entra en la misma cantidad y a la misma presión, se hace la aproximación de suponer una recirculación. En este modelo el aire de salida simplemente cede calor al ambiente y vuelve a entrar por la boca ya frío. En el diagrama PV esto corresponde a un enfriamiento a presión constante D→A.

Existen de hecho motores de turbina de gas en los que el fluido efectivamente recircula y solo el calor es cedido al ambiente. Para estos motores, el modelo del ciclo de Brayton ideal es más aproximado que para los de ciclo abierto.


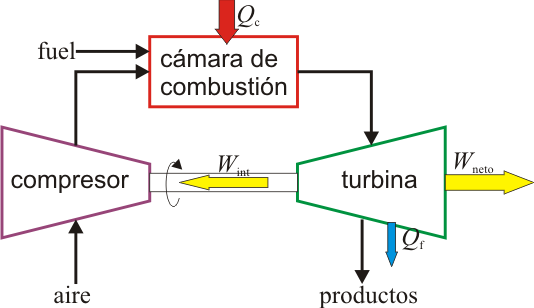
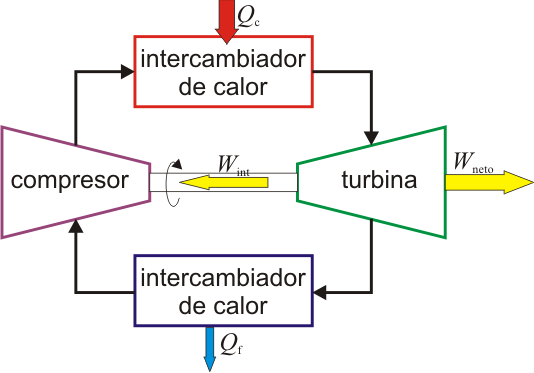
Motor de turbina de gas de ciclo abierto.	Motor de turbina de gas de ciclo cerrado.

3 Eficiencia en función del calor

3.1 Intercambio de calor

De los cuatro procesos que forman el ciclo cerrado, no se intercambia calor en los procesos adiabáticos A→B y C→D, por definición. Sí se intercambia en los dos procesos isóbaros.

En la combustión B→C, una cierta cantidad de calor $Q in$ (procedente de la energía interna del combustible) se transfiere al aire. Dado que el proceso sucede a presión constante, el calor coincide con el aumento de la entalpía

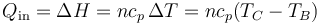
$Q_\mathrm{in} = \Delta H = nc_p\,\Delta T=nc_p(T_C-T_B)$

En la expulsión de los gases D→A el aire sale a una temperatura mayor que a la entrada, liberando posteriormente un calor $Q out$ al ambiente. En el modelo de sistema cerrado, en el que nos imaginamos que es el mismo aire el que se comprime una y otra vez en el motor, modelamos esto como que el calor $Q out$ es liberado en el proceso D→A, por enfriamiento. Su valor, análogamente al caso anterior, es

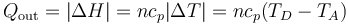
$Q_\mathrm{out}= |\Delta H| = nc_p|\Delta T|=nc_p(T_D-T_A)\,$

El valor absoluto viene de que, siendo un calor que sale del sistema al ambiente, la variación de entalpía es negativa.

3.2 Trabajo realizado

En este ciclo (a diferencia de lo que ocurre en el ciclo Otto) se realiza trabajo en los cuatro procesos. En dos de ellos el trabajo es positivo y en dos es negativo.

En la compresión de la mezcla A→B, se realiza un trabajo positivo sobre el gas. Al ser un proceso adiabático, todo este trabajo se invierte en incrementar la energía interna, elevando su temperatura:

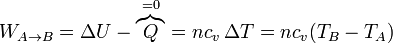
$W_{A\to B} = \Delta U - \overbrace{Q}^{=0} = nc_v\,\Delta T=nc_v(T_B-T_A)$

Este trabajo es positivo, es decir, es un trabajo que entra en el sistema

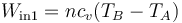
$W_\mathrm{in1}=nc_v(T_B-T_A)\,$

En la combustión el gas se expande a presión constante, por lo que el trabajo es igual a la presión por el incremento de volumen, cambiado de signo:

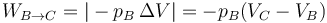
$W_{B\to C} = |-p_B\,\Delta V| = -p_B(V_C-V_B)\,$

Este trabajo es negativo, ya que es el aire, al expandirse, el que realiza el trabajo. Si lo expresamos como un trabajo que sale del sistema

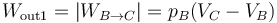
$W_\mathrm{out1}=|W_{B\to C}| = p_B(V_C-V_B)\,$

Aplicando la ecuación de los gases ideales y que

p B = p C

, podemos escribir este trabajo como

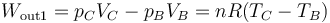
$W_\mathrm{out1} = p_CV_C-p_BV_B = nR(T_C-T_B)\,$

En la expansión C→D es el aire el que realiza trabajo sobre el pistón. De nuevo este trabajo útil equivale a la variación de la energía interna

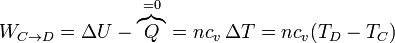
$W_{C\to D} = \Delta U - \overbrace{Q}^{=0} = nc_v\,\Delta T=nc_v(T_D-T_C)$

este trabajo es negativo, por ser el sistema el que lo realiza. Expresándolo como un trabajo que sale

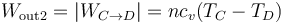
$W_\mathrm{out2}=|W_{C\to D}| = nc_v(T_C-T_D)\,$

En el enfriamiento en el exterior tenemos una compresión a presión constante:

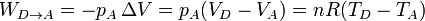
$W_{D\to A} = -p_A\,\Delta V = p_A(V_D-V_A)=nR(T_D-T_A)$

que es un trabajo positivo

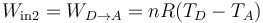
$W_\mathrm{in2}=W_{D\to A}=nR(T_D-T_A)\,$

El trabajo neto realizado por el gas es la diferencia entre el que sale y el que entra

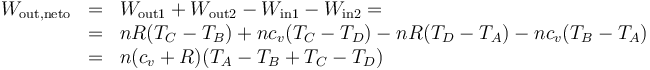
$\begin{array}{rcl}W_\mathrm{out,neto} & = & W_\mathrm{out1}+W_\mathrm{out2}-W_\mathrm{in1}-W_\mathrm{in2}= \\ & = & nR(T_C-T_B)+nc_v(T_C-T_D)-nR(T_D-T_A)-nc_v(T_B-T_A)\\ & = & n(c_v+R)(T_A-T_B+T_C-T_D)\end{array}$

Aplicando la ley de Mayer

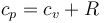
$c_p = c_v+R\,$

este trabajo se puede expresar como

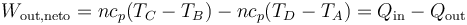
$W_\mathrm{out,neto}=nc_p(T_C-T_B)-nc_p(T_D-T_A)=Q_\mathrm{in}-Q_\mathrm{out}\,$

Por tratarse de un proceso cíclico, la variación de la energía interna es nula al finalizar el ciclo. Esto implica que el calor neto introducido en el sistema es igual al trabajo neto realizado por este, en valor absoluto.

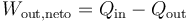
$W_\mathrm{out,neto} = Q_\mathrm{in}-Q_\mathrm{out}\,$

3.3 Rendimiento

El rendimiento de una máquina térmica se define, en general como “lo que sacamos dividido por lo que nos cuesta”. En este caso, lo que sacamos es el trabajo neto útil, $W out,neto$ . Lo que nos cuesta es el calor $Q in$ , que introducimos en la combustión. No podemos restarle el calor $Q out$ ya que ese calor se cede al ambiente y no es reutilizado (lo que violaría el enunciado de Kelvin-Planck). Por tanto

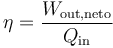
$\eta = \frac{W_\mathrm{out,neto}}{Q_\mathrm{in}}$

Sustituyendo el trabajo como diferencia de calores

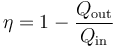
$\eta = 1-\frac{Q_\mathrm{out}}{Q_\mathrm{in}}$

Esta es la expresión general del rendimiento de una máquina térmica.

4 Eficiencia en función de las temperaturas

Sustituyendo las expresiones del calor que entra en el sistema, $Q in$ , y el que sale de él, $Q out$ , obtenemos la expresión del rendimiento

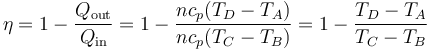
$\eta = 1-\frac{Q_\mathrm{out}}{Q_\mathrm{in}}= 1 - \frac{nc_p(T_D-T_A)}{nc_p(T_C-T_B)}=1-\frac{T_D-T_A}{T_C-T_B}$

Vemos que el rendimiento no depende de la cantidad de aire que haya en la cámara, ya que $n$ se cancela.

Para simplificar esta expresión sacamos factor común en primer lugar

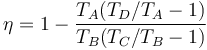
$\eta = 1 - \frac{T_A(T_D/T_A-1)}{T_B(T_C/T_B - 1)}$

Ahora debemos aplicar las relaciones entre las distintas temperaturas. Esto lo conseguimos escribiendo las ecuaciones que describen cada uno de los procesos del ciclo.

Compresión adiabática: Aumenta la temperatura según la ley de Poisson

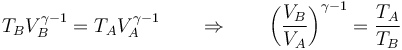
$T_BV_B^{\gamma-1}=T_AV_A^{\gamma-1}\qquad\Rightarrow\qquad \left(\frac{V_B}{V_A}\right)^{\gamma-1} =\frac{T_A}{T_B}$

Combinándola con la ley de los gases ideales queda

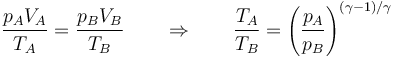
$\frac{p_AV_A}{T_A}=\frac{p_BV_B}{T_B}\qquad\Rightarrow\qquad \frac{T_A}{T_B}=\left(\frac{p_A}{p_B}\right)^{(\gamma-1)/\gamma}$

Combustión: Al ser a presión constante

$p_B=p_C\,$

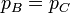
Expansión adiabática: Operando del mismo modo que en la compresión

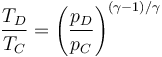
$\frac{T_D}{T_C}=\left(\frac{p_D}{p_C}\right)^{(\gamma-1)/\gamma}$

Escape: la salida y la entrada son ambas a la presión atmosférica

$p_D=p_A\,$

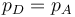
Combinando estas cuatro ecuaciones nos queda

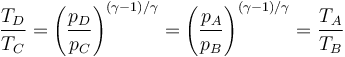
$\frac{T_D}{T_C}=\left(\frac{p_D}{p_C}\right)^{(\gamma-1)/\gamma}=\left(\frac{p_A}{p_B}\right)^{(\gamma-1)/\gamma}=\frac{T_A}{T_B}$

y por tanto

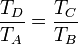
$\frac{T_D}{T_A}=\frac{T_C}{T_B}$

lo que nos simplifica el rendimiento a

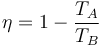
$\eta = 1 - \frac{T_A}{T_B}$

es decir que, como en el ciclo Otto, depende exclusivamente de la relación entre las temperaturas al principio y al final de la compresión, y no de cuánto se calienta en la combustión.

Puesto que $T B < T C$ , siendo $T C$ la temperatura máxima que alcanza el aire, vemos ya que este ciclo va a tener un rendimiento menor que un ciclo de Carnot que opere entre esas las temperaturas $T A$ y $T C$ .

5 Eficiencia en función de la relación de presión

Aplicando de nuevo la relación de Poisson

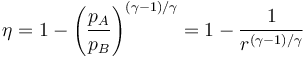
$\eta = 1 - \left(\frac{p_A}{p_B}\right)^{(\gamma-1)/\gamma} = 1 - \frac{1}{r^{(\gamma-1)/\gamma}}$

con $r = p B / p A$ la relación de presión entre la presión final y la inicial.

La eficiencia teórica de un ciclo Brayton depende, por tanto, exclusivamente de la relación de presiones. Para un valor típico de 8 esta eficiencia es del 44.8%.

6 Caso práctico

Como caso concreto, consideraremos una central eléctrica de turbina de gas que opera en un ciclo Brayton ideal y tiene una relación de presión de 8. La temperatura del gas es de 300 K en la entrada del compresor y de 1300 K en la entrada de la turbina. Determinaremos la temperatura del gas a la salida del compresor y de la turbina, y la eficiencia de esta turbina.

6.1 Eficiencia

La eficiencia de este ciclo es

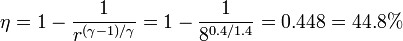
$\eta = 1-\frac{1}{r^{(\gamma-1)/\gamma}} = 1 - \frac{1}{8^{0.4/1.4}} = 0.448 = 44.8\%$

Esto quiere decir que más de la mitad del calor que entra en el ciclo ideal es disipada al exterior y solo un 45% es aprovechado como trabajo. En una turbina real la eficiencia es aun más baja.

6.2 Temperaturas

Inicialmente (estado A) tenemos gas que entra a 300 K y 101.3 kPa de presión.

$T_A=300\,\mathrm{K}\qquad\qquad p_A=100\,\mathrm{kPa}$

El volumen por cada mol de gas que entra sale de la ley de los gases ideales

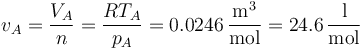
$v_A=\frac{V_A}{n}=\frac{RT_A}{p_A}=0.0246\,\frac{\mathrm{m}^3}{\mathrm{mol}}=24.6\,\frac{\mathrm{l}}{\mathrm{mol}}$

A la salida del compresor, la presión de ha multiplicado por 8 (la relación de compresión)

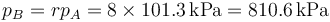
$p_B=rp_A=8\times 101.3\,\mathrm{kPa}=810.6\,\mathrm{kPa}$

La temperatura a la salida del compresor, $T B$ , puede calcularse empleando la ley de Poisson

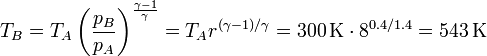
$T_B = T_A\left(\frac{p_B}{p_A}\right)^\frac{\gamma-1}{\gamma} = T_A r^{(\gamma-1)/\gamma} = 300\,\mathrm{K}\cdot 8^{0.4/1.4} = 543\,\mathrm{K}$

Vemos que la compresión incrementa la temperatura en 243 K, mientras que la combustión lo hace en (1300−543) K = 757 K, más del triple que la compresión.

El volumen molar a la salida del compresor es

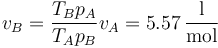
$v_B=\frac{T_Bp_A}{T_Ap_B}v_A=5.57\,\frac{\mathrm{l}}{\mathrm{mol}}$

A la entrada de la turbina, C, la presión es la misma que en B, y la temperatura ha subido a 1300 K, lo que implica un aumento del volumen molar

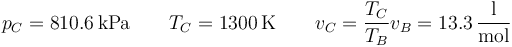
$p_C=810.6\,\mathrm{kPa}\qquad T_C = 1300\,\mathrm{K}\qquad v_C=\frac{T_C}{T_B}v_B=13.3\,\frac{\mathrm{l}}{\mathrm{mol}}$

Del mismo modo se calcula la temperatura a la salida de la turbina

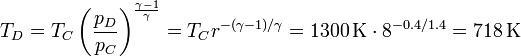
$T_D = T_C\left(\frac{p_D}{p_C}\right)^\frac{\gamma-1}{\gamma} = T_C r^{-(\gamma-1)/\gamma} = 1300\,\mathrm{K}\cdot 8^{-0.4/1.4} = 718\,\mathrm{K}$

El gas a la salida está a una temperatura muy superior a la del ambiente, por lo que la entrega de calor al foco frío es muy importante.

El volumen molar a la salida lo podemos obtener también por la ley de los gases ideales

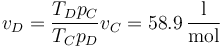
$v_D = \frac{T_Dp_C}{T_Cp_D}v_C=58.9\,\frac{\mathrm{l}}{\mathrm{mol}}$

Tabulando todos estos valores

Estado	p (kPa)	T (K)	v (l/mol)
A	101.3	300	24.6
B	810.6	543	5.57
C	810.6	1300	13.3
D	101.3	718	58.9

7 Motores de reacción

El ciclo Brayton descrito aquí sirve para modelar el comportamiento de un motor de turbina que mueve una hélice, pero no para un motor a reacción.

La diferencia es que:

En un avión de hélice interesa obtener el máximo trabajo neto que puede dar la turbina, para mover la hélice.

En el motor a reacción, en cambio, interesa obtener el mínimo, que es el que mantiene en marcha el compresor (y resto de sistemas de la aeronave). El resto de la energía interna aprovechable no se extrae del gas, sino que se mantiene en él, en forma de energía cinética. La cantidad de movimiento que se llevan los gases expulsados es lo que impulsa al avión hacia adelante, de acuerdo con la tercera ley de Newton.

Puesto que el trabajo neto en un avión a reacción es cero, su eficiencia se define no por el trabajo realizado, sino por la potencia de propulsión dividida por el calor inyectado por unidad de tiempo.

8 Enlaces

Artículo sobre el ciclo Brayton en el curso de Termodinámica del MIT.

Ciclo Brayton (GIE)

De Laplace

Contenido

1 Enunciado

2 Descripción del ciclo

3 Eficiencia en función del calor

3.1 Intercambio de calor

3.2 Trabajo realizado

3.3 Rendimiento

4 Eficiencia en función de las temperaturas

5 Eficiencia en función de la relación de presión

6 Caso práctico

6.1 Eficiencia

6.2 Temperaturas

7 Motores de reacción

8 Enlaces

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES