Ciclo de Carnot (GIE)

De Laplace

Contenido

1 Introducción
2 Ciclo de Carnot
3 Rendimiento de un ciclo de Carnot
- 3.1 Para un gas ideal
- 3.2 Valores típicos
4 Refrigerador de Carnot

1 Introducción

El teorema de Carnot establece que el rendimiento de una máquina térmica es siempre menor o igual que el de una máquina térmica reversible que opere entre las mismas temperaturas.

Como corolario, el rendimiento de todas las máquinas térmicas reversibles que operen entre las mismas temperaturas es el mismo, independientemente del sistema físico que corresponda a la máquina. Puede ser un gas ideal sometido a compresiones o expansiones, puede ser un material paramagnético sometido a campos magnéticos variables, puede ser un sistema bifásico formado por agua y vapor de agua… el resultado es siempre el mismo.

Este resultado, ya de por sí bastante contundente, nos permite además calcular el rendimiento máximo que puede tener una máquina térmica. Nos basta con diseñar una máquina térmica reversible y hallar su rendimiento. El de todas las demás reversibles será el mismo, y el de las irreversibles será menor.

Existen varias posibilidades: el ciclo de Carnot, el ciclo Stirling o el ciclo Ericcson, por ejemplo. Aquí describiremos el ciclo de Carnot, que es el más importante de ellos.

2 Ciclo de Carnot

2.1 Procesos

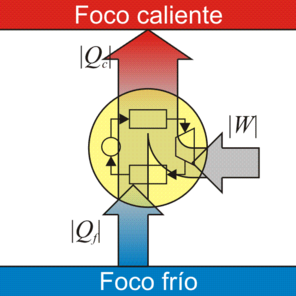
Para conseguir la máxima eficiencia la máquina térmica que estamos diseñando debe tomar calor de un foco caliente, cuya temperatura es como máximo $T c$ y verter el calor de desecho en el foco frío, situado como mínimo a una temperatura $T f$ .

Para que el ciclo sea óptimo, todo el calor absorbido debería tomarse a la temperatura máxima, y todo el calor de desecho, cederse a la temperatura mínima. Por ello, el ciclo que estamos buscando debe incluir dos procesos isotermos, uno de absorción de calor a $T c$ y uno de cesión a $T f$ .

Para conectar esas dos isotermas (esto es, para calentar el sistema antes de la absorción y enfriarlo antes de la cesión), debemos incluir procesos que no supongan un intercambio de calor con el exterior (ya que todo el intercambio se produce en los procesos isotermos). La forma más sencilla de conseguir esto es mediante dos procesos adiabáticos reversibles (no es la única forma, el motor de Stirling utiliza otro método, la recirculación). Por tanto, nuestra máquina térmica debe constar de cuatro pasos:

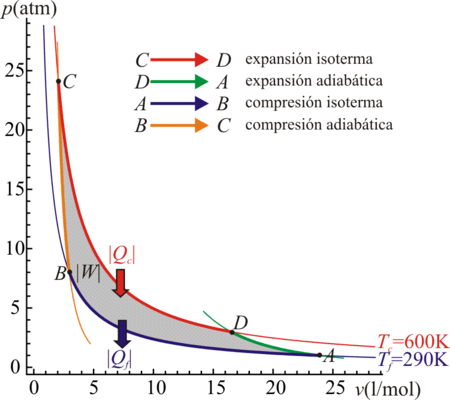
C→D Absorción de calor $Q in = Q c$ en un proceso isotermo a temperatura $T c$ .

D→A Enfriamiento adiabático hasta la temperatura del foco frío, $T f$ .

A→B Cesión de calor $Q out = | Q f |$ al foco frío a temperatura $T f$ .

B→C Calentamiento adiabático desde la temperatura del foco frío, $T f$ a la temperatura del foco caliente, $T c$ .

2.2 Gases ideales

Como ejemplo de Ciclo de Carnot consideraremos el caso de una máquina térmica compuesta por un gas ideal situado en el interior de un cilindro con un pistón. Para que el ciclo sea reversible debemos suponer que no existe fricción en el sistema y todos los procesos son cuasiestáticos.

Para un sistema de este tipo los cuatro pasos son los siguientes:

Expansión isoterma C→D: El gas se pone en contacto con el foco caliente a $T c$ y se expande lentamente. Se extrae trabajo del sistema, lo que provocaría un enfriamiento a una temperatura ligeramente inferior a $T c$ , que es compensado por la entrada de calor $Q in$ desde el baño térmico. Puesto que la diferencia de temperaturas entre el baño y el gas es siempre diferencial, este proceso es reversible. De esta manera la temperatura permanece constante. En el diagrama pV, los puntos de este paso están sobre una hipérbola dada por la ley de los gases ideales

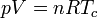
$pV=nRT_c\,$

Expansión adiabática D→A: El gas se aísla térmicamente del exterior y se continúa expandiendo. Se está realizando un trabajo adicional, que ya no es compensado por la entrada de calor del exterior. El resultado es un enfriamiento según una curva dada por la ley de Poisson

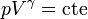
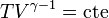
$pV^\gamma=\mathrm{cte}\,$ $\Rightarrow$ $TV^{\gamma-1}=\mathrm{cte}\,$

Compresión isoterma A→B: Una vez que ha alcanzado la temperatura del foco frío, el gas vuelve a ponerse en contacto con el exterior (que ahora es un baño a temperatura $T f$ ). Al comprimirlo el gas tiende a calentarse ligeramente por encima de la temperatura ambiente, pero la permeabilidad de las paredes permite evacuar calor al exterior, de forma que la temperatura permanece constante. Esta paso es de nuevo una hipérbola según la lay de los gases ideales.

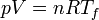
$pV=nRT_f\,$

Compresión adiabática B→C: El gas se vuelve a aislar térmicamente y se sigue comprimiendo. La temperatura sube como consecuencia del trabajo realizado sobre el gas, que se emplea en aumentar su energía interna. Los puntos de este camino están unidos por una curva dada por la ley de Poisson

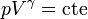
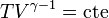
$pV^\gamma=\mathrm{cte}\,$ $\Rightarrow$ $TV^{\gamma-1}=\mathrm{cte}\,$

2.3 Otros sistemas

2.4 Representación en un diagrama T-S

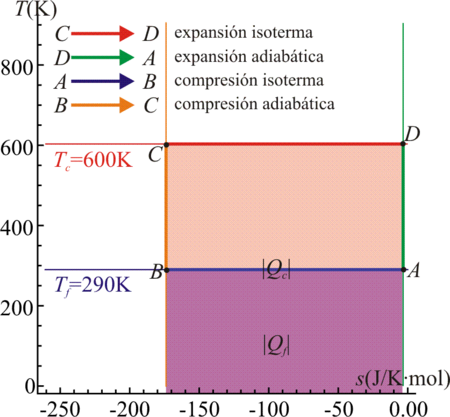
El ciclo de Carnot adopta una representación especialmente sencilla si en lugar de un diagrama pV se representa en uno TS que tiene por eje de abscisas la entropía del sistema y por eje de ordenadas la temperatura de éste.

En un diagrama TS, los procesos isotermos son simplemente rectas horizontales. Los procesos adiabáticos que, por ser reversibles, son a entropía constante, son rectas verticales. Esto quiere decir que a un ciclo de Carnot le corresponde simplemente un rectángulo, independientemente de que el ciclo sea producido actuando sobre un gas ideal o sobre cualquier otro sistema.

En este diagrama el calor absorbido $Q c$ es el área del rectángulo delimitado por el lado superior del ciclo y el eje de abscisas, mientras que el calor cedido $| Q f |$ es el área del rectángulo definido por el lado inferior del ciclo y el eje de abscisas. El calor neto, $| Q c | - | Q f |$ , que entra en el sistema es el área del rectángulo delimitado por el ciclo. Por el Primer Principio, este área equivale al trabajo neto efectuado por el sistema, $| W |$ .

Si en vez de una máquina de Carnot tenemos un refrigerador de Carnot, la figura es exactamente la misma, solo que se recorren en sentido opuesto.

3 Rendimiento de un ciclo de Carnot

3.1 Para un gas ideal

Puesto que son idénticos todos los rendimientos de máquinas que operen según el ciclo de Carnot, podemos emplear la que nos resulte más simple para calcular este rendimiento.

La elección natural es emplear el ciclo de un gas ideal descrito anteriormente.

El rendimiento de una máquina térmica es

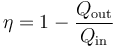
$\eta = 1 - \frac{Q_\mathrm{out}}{Q_\mathrm{in}}$

En el caso del gas ideal, el calor $Q in$ es el absorbido en una expansión isoterma, en la cual no varía la energía interna

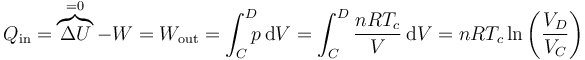
$Q_\mathrm{in} = \overbrace{\Delta U}^{=0}-W = W_\mathrm{out}=\int_C^D\!\!\!p\,\mathrm{d}V = \int_C^D \frac{nRT_c}{V}\,\mathrm{d}V = nRT_c\ln\left(\frac{V_D}{V_C}\right)$

El calor $Q out$ es el cedido en una compresión isoterma, en la que tampoco varía la energía interna

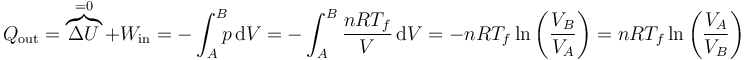
$Q_\mathrm{out} = \overbrace{\Delta U}^{=0}+W_\mathrm{in} = -\int_A^B\!\!\!p\,\mathrm{d}V = -\int_A^B \frac{nRT_f}{V}\,\mathrm{d}V =-nRT_f\ln\left(\frac{V_B}{V_A}\right)= nRT_f\ln\left(\frac{V_A}{V_B}\right)$

Por tanto, el rendimiento es igual a

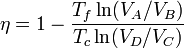
$\eta = 1 - \frac{T_f\ln(V_A/V_B)}{T_c\ln(V_D/V_C)}$

Este no puede ser el resultado final pues depende de algo específico del ciclo de gas, como son los volúmenes en los distintos estados. Si todos rendimientros de máquinas reversibles que actúan entre las mismas temperaturas son iguales debe quedarnos una función que dependa exclusivamente de $T c$ y $T f$ .

Conseguimos esto observando que el paso de $T f$ a $T c$ es una compresión adiabática, en la que la temperatura aumenta al reducirse el volumen, según la ley de Poisson

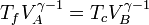
$T_fV_A^{\gamma-1} = T_cV_B^{\gamma-1}$

Análogamente, para el enfriamiento adiabático la temperatura disminuye al aumentar el volumen

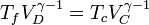
$T_fV_D^{\gamma-1} = T_cV_C^{\gamma-1}$

Dividiendo la segunda ecuación por la primera queda

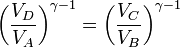
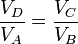
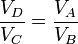
$\left(\frac{V_D}{V_A}\right)^{\gamma-1}=\left(\frac{V_C}{V_B}\right)^{\gamma-1}$ $\Rightarrow$ $\frac{V_D}{V_A}=\frac{V_C}{V_B}$ $\Rightarrow$ $\frac{V_D}{V_C}=\frac{V_A}{V_B}$

Esto implica que los logaritmos que aparecen en el numerador y el denominador del rendimiento son iguales y éste se simplifica a

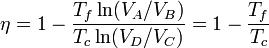
$\eta = 1 - \frac{T_f\ln(V_A/V_B)}{T_c\ln(V_D/V_C)}=1 - \frac{T_f}{T_c}$

Lo que vale para el ciclo de Carnot vale para todas las máquina térmicas reversible que operan entre solo dos focos térmicos. El rendimiento, para todas ellas, es igual a

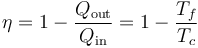
$\eta = 1 - \frac{Q_\mathrm{out}}{Q_\mathrm{in}}=1 - \frac{T_f}{T_c}$

3.2 Valores típicos

El teorema de Carnot establece que el rendimiento máximo que puede tener una máquina térmica lo da el ciclo de Carnot. Pero, ¿cuanto es ese valor máximo? ¿Ronda acaso el 90%, el 80%, el 50%, el 5%? La respuesta es que naturalmente, depende. Según variemos las temperaturas de los focos, así cambiará el rendimiento.

Supongamos una máquina que trabaja entre dos focos térmicos: uno es agua en equilibrio con vapor de agua, a 100°C, y el otro es agua en equilibrio con hielo, a 0°C. Para esta máquina

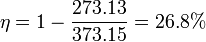
$\eta = 1 - \frac{273.13}{373.15} = 26.8\%$

es decir, de todo el calor que toma, solo la cuarta parte se aprovecha como trabajo. Las tres cuartas partes restantes se desperdician como calor de desecho. Vemos que el rendimiento máximo puede ser de hecho muy bajo.

Puesto que una máquina real posee factores irreversibles que reducen el rendimiento aun más, podemos llegar a que una máquina térmica, aunque posible, no sea de interés por su bajo rendimiento. Por ejemplo, imaginemos un gran estanque de agua puesto al sol. Podríamos aprovechar la evaporación por la acción del sol para mover una turbina. Esto sería un generador sencillo de fabricar y además con combustible “gratis”. Sin embargo su eficiencia puede ser del 5% o menor, esto es, que se produce como 20 veces más calor de desecho que trabajo útil se saca.

De la expresión del rendimiento para el ciclo de Carnot se ve que la forma de mejorar la eficiencia es elevando la temperatura del foco caliente o reduciendo la del frío. Puesto que ni la primera puede hacerse infinita ni la segunda nula (por el tercer principio de la termodinámica), un rendimiento del 100% nunca es posible.

Comparemos ahora el rendimiento de un ciclo de Carnot con otro, como el ciclo Otto. En un caso práctico de este ciclo se considera un motor con una relación de compresión $r = 8$ . Para este ciclo

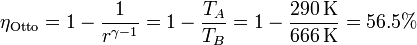
$\eta_\mathrm{Otto} = 1 - \frac{1}{r^{\gamma-1}} = 1 - \frac{T_A}{T_B} = 1- \frac{290\,\mathrm{K}}{666\,\mathrm{K}}= 56.5\%$

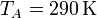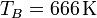siendo $T_A=290\,\mathrm{K}$ y $T_B=666\,\mathrm{K}$ las temperaturas al principio y al final de la subida del pistón (compresión adiabática). Esta temperatura $T B$ , no obstante, no es la máxima a la que trabaja el motor. La temperatura máxima se alcanza tras la combustión de la gasolina. Para el mismo caso práctico, esa temperatura es

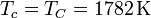
$T_c = T_C = 1782\,\mathrm{K}$

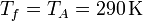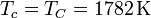El rendimiento de una máquina de Carnot que trabaje entre las temperaturas $T_f = T_A=290\,\mathrm{K}$ y $T_c = T_C = 1782\,\mathrm{K}$ es

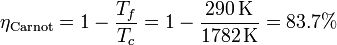
$\eta_\mathrm{Carnot}=1-\frac{T_f}{T_c} = 1- \frac{290\,\mathrm{K}}{1782\,\mathrm{K}}= 83.7\%$

Vemos que el ciclo de Carnot es mucho más eficiente que el ciclo Otto, cuyo rendimiento es un 70% del de Carnot.

4 Refrigerador de Carnot

Al ser un ciclo reversible, podemos invertir cada uno de los procesos y convertir la máquina de Carnot en un refrigerador. Este refrigerador extrae una cierta cantidad de calor

| Q f |

del foco frío, requiriendo para ello una cierta cantidad de trabajo

| W |

, arrojando una cantidad de calor

| Q c |

en el foco caliente.

El coeficiente de desempeño de un refrigerador reversible como el de Carnot es

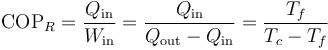
$\mathrm{COP}_R = \frac{Q_\mathrm{in}}{W_\mathrm{in}} = \frac{Q_\mathrm{in}}{Q_\mathrm{out}-Q_\mathrm{in}} = \frac{T_f}{T_c-T_f}$

ya que, como en la máquina de Carnot, la cantidad de calor intercambiada con cada foco es proporcional a la temperatura de dicho foco.

Para un refrigerador que trabaje entre una temperatura de 5°C y 22°C, este coeficiente de desempeño vale

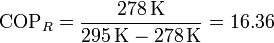
$\mathrm{COP}_R = \frac{278\,\mathrm{K}}{295\,\mathrm{K}-278\,\mathrm{K}} = 16.36$

Este valor es el máximo que puede alcanzar un refrigerador real, aunque los valores prácticos del COP están muy por debajo de esta cantidad.

Si el refrigerador de Carnot se considera como una bomba de calor, su coeficiente de desempeño es

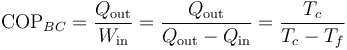
$\mathrm{COP}_{BC} = \frac{Q_\mathrm{out}}{W_\mathrm{in}} = \frac{Q_\mathrm{out}}{Q_\mathrm{out}-Q_\mathrm{in}} = \frac{T_c}{T_c-T_f}$

que para los mismos valores de las temperaturas de los focos nos da

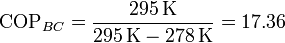
$\mathrm{COP}_{BC} = \frac{295\,\mathrm{K}}{295\,\mathrm{K}-278\,\mathrm{K}} = 17.36$

también muy por encima de los valores reales de las bombas de calor.

Ciclo de Carnot (GIE)

De Laplace

Contenido

1 Introducción

2 Ciclo de Carnot

2.1 Procesos

2.2 Gases ideales

2.3 Otros sistemas

2.4 Representación en un diagrama T-S

3 Rendimiento de un ciclo de Carnot

3.1 Para un gas ideal

3.2 Valores típicos

4 Refrigerador de Carnot

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES