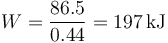Consumo de un refrigerador

De Laplace

Contenido

1 Enunciado
2 Calor que entra
3 Trabajo mínimo
4 Producción de entropía
5 Trabajo para fabricar cubitos

1 Enunciado

Se tiene un congelador en forma de cubo de 60 cm×60 cm×60 cm cuyas paredes son de fibra de vidrio de 4 cm de grosor. La temperatura interior del congelador es −3 °C y la exterior es de +22 °C

¿Cuánto vale aproximadamente el calor que entra en el congelador por segundo?
¿Cuál es el trabajo por segundo mínimo necesario para hacer funcionar este congelador y mantener constante la temperatura interior?
Suponga que la potencia real necesaria para hacerlo funcionar es de 123 W. ¿Cuánto es la producción de entropía por segundo en el universo debida a este refrigerador?
Suponga que se introduce en el congelador una cubitera con 200 g de agua a temperatura ambiente. ¿Cuánto trabajo debe introducirse en el congelador para fabricar los cubitos?

Datos: Conductividad térmica de la fibra de vidrio: 0.04 W/(m·K); Calor específico del agua: 4.18 kJ/(kg·K); Calor específico del hielo: 2.09 kJ/(kg·K); Entalpía específica de fusión del agua: 334 kJ/kg.

2 Calor que entra

Al haber una pared sólida, el calor entra en el frigorífico por conducción, cumpliéndose la ley de Fourier

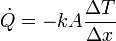
$\dot{Q}=-kA\frac{\Delta T}{\Delta x}$

En este caso, $k$ es la conductividad térmica de la fibra de vidrio, $Δ x$ es el espesor de la pared, $Δ T$ es la diferencia de temperaturas entre el exterior y el interior y $A$ es el área del cubo, que es igual a 6 veces el área de una cara, es decir

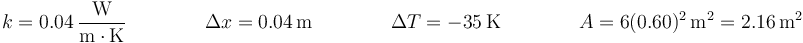
$k = 0.04\,\frac{\mathrm{W}}{\mathrm{m}\cdot\mathrm{K}}\qquad\qquad \Delta x = 0.04\,\mathrm{m}\qquad\qquad \Delta T = -35\,\mathrm{K}\qquad\qquad A = 6(0.60)^2\,\mathrm{m}^2 = 2.16\,\mathrm{m}^2$

lo que nos da

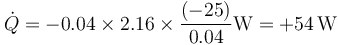
$\dot{Q}=-0.04\times 2.16\times\frac{(-25)}{0.04}\mathrm{W}=+54\,\mathrm{W}$

Resulta un calor positivo, ya que va hacia el interior del congelador.

3 Trabajo mínimo

El trabajo mínimo se obtiene suponiendo que el refrigerador es uno reversible, cuyo coeficiente de desempeño vale

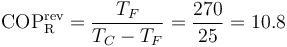
$\mathrm{COP}^\mathrm{rev}_\mathrm{R}=\frac{T_F}{T_C-T_F}=\frac{270}{25}=10.8$

lo que nos da un trabajo mínimo por segundo

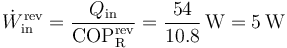
$\dot{W}^\mathrm{rev}_\mathrm{in}=\frac{Q_\mathrm{in}}{\mathrm{COP}^\mathrm{rev}_\mathrm{R}}=\frac{54}{10.8}\,\mathrm{W}=5\,\mathrm{W}$

4 Producción de entropía

Tenemos dos producciones de entropía: la debida a la trasferencia de calor y la debida al funcionamiento del refrigerador.

4.1 Entropía por transferencia de calor

Debido a la conducción, hay un calor 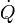$\dot{Q}$ que está saliendo de un foco a 22°C (en el cual, por tanto, disminuye la entropía) y está entrando en otro a −3°C (en el cual aumenta). La producción de entropía por segundo debida a este proceso es

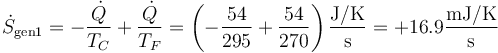
$\dot{S}_\mathrm{gen1}=-\frac{\dot{Q}}{T_C}+\frac{\dot{Q}}{T_F}=\left(-\frac{54}{295}+\frac{54}{270}\right)\frac{\mathrm{J}/\mathrm{K}}{\mathrm{s}}=+16.9\frac{\mathrm{mJ}/\mathrm{K}}{\mathrm{s}}$

4.2 Entropía por funcionamiento del refrigerador

Del mismo modo, al funcionar el refrigerador, toma una cierta cantidad de calor del foco frío y expulsa otra en el foco caliente.

La cantidad de calor expulsada por segundo es

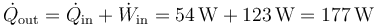
$\dot{Q}_\mathrm{out}=\dot{Q}_\mathrm{in}+\dot{W}_\mathrm{in}=54\,\mathrm{W}+123\,\mathrm{W}=177\,\mathrm{W}$

lo que da una producción de entropía

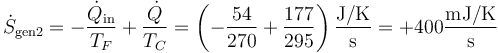
$\dot{S}_\mathrm{gen2}=-\frac{\dot{Q}_\mathrm{in}}{T_F}+\frac{\dot{Q}}{T_C}=\left(-\frac{54}{270}+\frac{177}{295}\right)\frac{\mathrm{J}/\mathrm{K}}{\mathrm{s}}=+400\frac{\mathrm{mJ}/\mathrm{K}}{\mathrm{s}}$

4.3 Producción total de entropía

Sumando los dos términos

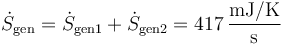
$\dot{S}_\mathrm{gen}=\dot{S}_\mathrm{gen1}+\dot{S}_\mathrm{gen2} = 417\,\frac{\mathrm{mJ}/\mathrm{K}}{\mathrm{s}}$

Es fácil ver que la producción total de entropía es igual a

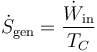
$\dot{S}_\mathrm{gen}=\frac{\dot{W}_\mathrm{in}}{T_C}$

5 Trabajo para fabricar cubitos

Para fabricar cubitos de hielo debemos llevar lo 0.20kg de agua al estado de hielo a -3°C.

El calor que hay que extraer para ello es igual a

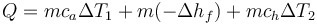
$Q=mc_a\Delta T_1+m(-\Delta h_f)+mc_h\Delta T_2\,$

es decir, suma del calor que hay que extraer para llevar el agua hasta 0°C, luego para convertirla en hielo y luego àra enfriar la temperatura de éste. El resultado es

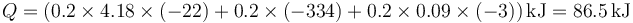
$Q=\left(0.2\times 4.18\times(-22)+0.2\times(-334)+0.2\times 0.09\times(-3)\right)\mathrm{kJ}=86.5\,\mathrm{kJ}$

Para extraer este calor neceistamos un trabajo

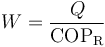
$W=\frac{Q}{\mathrm{COP}_\mathrm{R}}$

siendo $COP R$ el coeficiente de desempeño real

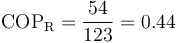
$\mathrm{COP}_\mathrm{R}=\frac{54}{123}=0.44$

lo que da un trabajo

$W=\frac{86.5}{0.44}=197\,\mathrm{kJ}$

Consumo de un refrigerador

De Laplace

Contenido

1 Enunciado

2 Calor que entra

3 Trabajo mínimo

4 Producción de entropía

4.1 Entropía por transferencia de calor

4.2 Entropía por funcionamiento del refrigerador

4.3 Producción total de entropía

5 Trabajo para fabricar cubitos

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES