De Laplace

Contenido 1 Problemas del boletín (2015/16) 1.1 Ecuaciones de curvas 1.2 Trayectoria de una partícula 1.3 Movimiento instantáneo de una partícula 1.4 Tiro oblicuo 1.5 Cañon lanzando partícula sobre un carrito deslizando sobre plano inclinado 1.6 Velocidad de un punto en la superficie de la Tierra 1.7 ppp 1.8 Parámetro arco y triedro intrínseco de una hélice 1.9 Movimiento oscilatorio armónico unidimensional 2 Otros problemas 2.1 Barra con extremos sobre los ejes 2.2 Barra girando en un plano 2.3 Barra deslizando sobre una circunferencia 2.4 Cuerda enrollándose 2.5 Cuerda sobre disco de radio variable 2.6 Disco girando con partícula suspendida de cuerda 2.7 Cuestión sobre cinemática de la partícula 2.8 Punto moviéndose sobre una parábola 2.9 Tiro parabólico sobre un plano inclinado 2.10 Partícula recorriendo una espiral 2.11 Partícula moviéndose sobre una parábola 2.12 Partícula con curvatura y aceleración tangencial dependientes del tiempo

1 Problemas del boletín (2015/16)

1.1 Ecuaciones de curvas

Expresa en forma parámetrica e implícita las siguientes curvas

1. El eje OY
2. Una circunferencia de radio a, contenida en el plano XY y con centro en el origen.
3. Una parábola contenida en el plano YZ y con ecuación z = y².

1.2 Trayectoria de una partícula

La trayectoria de una partícula viene dada por la ley horaria

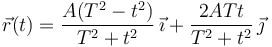
Determina la velocidad y aceleración de la partícula, los vectores del triedro intrínseco, así como la ecuación de la trayectoria. Calcula también las componentes intrínsecas de la velocidad y la aceleración ¿Cual es la expresión de un desplazamiento elemental 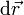? ¿Cuánto tiempo emplea en llegar al punto medio de la trayectoria?. ¿Y al punto final? Describe cualitativamente la evolución temporal de la posición de la partícula.

1.3 Movimiento instantáneo de una partícula

Una partícula P se mueve respecto de un sistema de referencia cartesiano OXYZ de manera que en un cierto instante t₀, su velocidad y su aceleración están descritas por los vectores

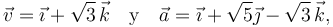
con sus componentes medidas en m / s y m / s², respectivamente. Determine, en el instante considerado, las siguientes magnitudes cinemáticas:

1. Módulo de la velocidad (celeridad) y su derivada.
2. Componente normal de la aceleración y radio de curvatura de la trayectoria.
3. Vector aceleración normal.

1.4 Tiro oblicuo

Determina el movimiento de un proyectil disparado con una velocidad inicial v₀ y un ángulo α con la horizontal. El proyectil está sometido a la acción de la gravedad. Calcula el radio de curvatura en el punto más alto de su trayectoria.

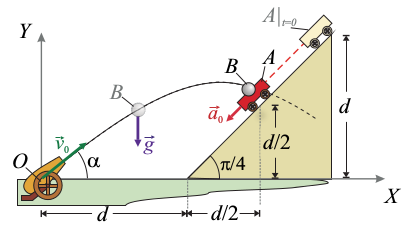
1.5 Cañon lanzando partícula sobre un carrito deslizando sobre plano inclinado

Un móvil A, que puede ser considerado como un cuerpo puntual, se desplaza por una ladera con una pendiente de 45^o respecto de la horizontal. El móvil desciende por la ladera realizando un movimiento rectilíneo uniformemente acelerado, siendo el módulo de su aceleración 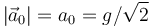. En el instante de iniciar el descenso el móvil se encuentra en reposo, a una altura d. Además, a una distancia d de la base de la ladera, en dirección horizontal, se halla emplazado un dispositivo lanzador de proyectiles a los que imprime una velocidad inicial de módulo v₀ y formando un ángulo α con la horizontal.

1. Encuentre la expresión de las ecuaciones horarias que describen el movimiento del móvil A respecto al sistema de referencia del dibujo.
2. En el instante en el que el móvil A inicia el descenso, el lanzado dispara un proyectil B que, a partir de entonces, se mueve con la aceleración debida a la acción de la gravedad, 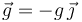, constante en módulo, dirección y sentido. ¿Qué valores deben tener el ángulo de lanzamiento α y la celeridad inicial v₀ del proyectil B para que éste impacte sobre el móvil A cuando se encuentra en la mitad de la ladera?

1.6 Velocidad de un punto en la superficie de la Tierra

La Tierra rota uniformemente con respecto a su eje con velocidad angular ω constante. Encuentra en función de la latitud λ, la velocidad y la aceleración de un punto sobre la superficie terrestre, debidas a dicha rotación (radio de la Tierra: 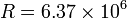m.)

1.7 ppp

1.8 Parámetro arco y triedro intrínseco de una hélice

Sea la hélice Γ descrita en un sistema de referencia cartesiano OXYZ por las siguientes ecuaciones paramétricas:

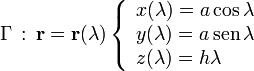
donde a y h son constantes conocidas.

1. Determina la longitud recorrida sobre la hélice (parámetro arco) en función del parámetro λ
2. Obtén los vectores del triedro intrínseco en cada punto de dicha curva.
3. Calcula su radio de curvatura.

 

1.9 Movimiento oscilatorio armónico unidimensional

Un punto inicialmente en reposo en la posición x = L describe un movimiento rectilíneo sobre el eje OX, de modo que su aceleración es de la forma a = − k²x. Determina en función del tiempo su posición y velocidad. ¿Cuál es la siguiente posición de reposo, y cuánto tiempo tarda en alcanzarla?

2 Otros problemas

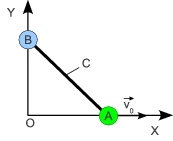
2.1 Barra con extremos sobre los ejes

Dos partículas, A y B, de masa m, están unidas por una barra rígida de longitud L y masa despreciable. La partícula A se mueve sobre el eje OX con velocidad uniforme v₀, mientras que la partícula B está obligada a moverse sobre el eje OY. Si en el instante t = 0 la partícula A se encontraba en el punto O

1. Encuentra la posición, velocidad y aceleración de la partícula B en función de v₀ y del tiempo.
2. ¿Cuál es el vector de posición y la velocidad del punto medio de la barra (C) en función de v₀ y t₀?
3. Describe la curva que corresponde a la trayectoria del punto medio de la barra.
4. ¿Que tipo de movimiento describe el punto medio de la barra? Razona tu respuesta.

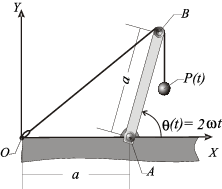
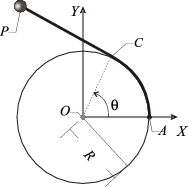
2.2 Barra girando en un plano

Una barra rígida AB de longitud 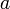se mueve en un plano vertical OXY, manteniendo su extremo A articulado en un punto del eje horizontal de coordenadas 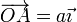, y verificando la ley horaria θ(t) = 2ωt, con 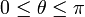y siendo ω = cte. Un hilo inextensible de longitud 2a tiene uno de sus extremos conectado al origen del sistema de referencia (punto O), mientras que del otro cuelga una partícula P que mantiene al hilo siempre tenso. El hilo se apoya sobre una pequeña polea de radio despreciable situada en el extremo B de la barra, de forma que el tramo 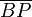permanece siempre paralelo al eje OY (ver figura). Se pide:

1. Ecuaciones horarias del punto .
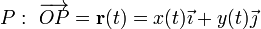2. Instante del tiempo t_M en que la partícula alcanza su altura máxima.
3. Radio de curvatura de la trayectoria seguida por P, en el instante considerado en el apartado anterior.

2.3 Barra deslizando sobre una circunferencia

En un plano OXY, se define el sistema cinemático formado por los dos siguientes elementos geométricos:

1. una circunferencia fija, de radio R y centrada en el punto C de coordenadas ;
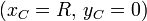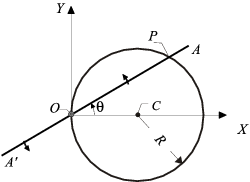
2. un segmento rectilíneo móvil A'A, de longitud superior a 4R, el cual gira con velocidad angular constante ω (en sentido antihorario) alrededor de un eje fijo que pasa por su punto medio O y es normal al plano OXY (eje OZ).

Sabiendo que el ángulo θ ( que forman OA y OX) es nulo en el instante inicial (t = 0); y considerando como móvil problema el punto P en el que se cortan el segmento A'A y la circunferencia , se pide:

1. item Determinar las ecuaciones horarias, 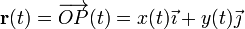, del punto P, así como sus vectores velocidad, 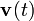, y aceleración, .
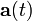2. Calcular las aceleraciones tangencial y normal de dicho punto P.

2.4 Cuerda enrollándose

Una partícula se mueve en el plano OXY mientras permanece conectada a uno de los extremos de un hilo inextensible de longitud 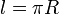. El otro extremo está unido a un punto fijo A de una circunferencia de radio R y centro O, cuyas coordenadas en el sistema cartesiano OXY son 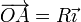. Partiendo de la posición inicial 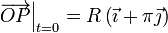, el movimiento de la partícula con velocidad de módulo constante v₀ da lugar a que el hilo, que permanece siempre tenso, se enrolle en dicha circunferencia. Utilizando como parámetro el ángulo θ correspondiente al punto C donde desaparece el contacto hilo--circunferencia, calcula:

1. Las ecuaciones paramétricas de la trayectoria seguida por la partícula.
2. La ley horaria del movimiento θ = θ(t) y tiempo que tarda el hilo en enrollarse completamente sobre la circunferencia.
3. La aceleración de la partícula.
4. El triedro intrínseco de la trayectoria seguida por la partícula

2.5 Cuerda sobre disco de radio variable

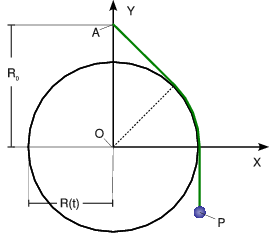
Un punto material P pende verticalmente del extremo de un hilo inextensible y permanentemente tenso. Este se apoya y desliza sobre una circunferencia de radio variable con el tiempo 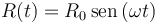en el intervalo 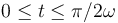(R₀ y ω son constantes conocidas), y centrada en el origen O de un sistema de referencia cartesiano OXY . La longitud total del hilo es l = πR₀ / 2, y su otro extremo se halla fijo en un punto A, tal que 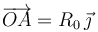(ver figura). Determina:

1. Las ecuaciones horarias cartesianas del punto P , y su posición final en el instante final t_f = π / 2ω.
2. Los vectores velocidad y aceleración de dicho punto en todo instante de tiempo.
3. La aceleración normal de P y el radio de curvatura de su trayectoria en todo instante de tiempo, así como la posición del centro de curvatura de la trayectoria en el instante inicial.

2.6 Disco girando con partícula suspendida de cuerda

El mecanismo de la figura consiste en un disco de radio R, siempre contenido en el plano vertical OXY, que se mueve girando alrededor de un punto de su perímetro que coincide con el origen O del sistema de referencia. El movimiento del disco está descrito por la ley horaria θ(t) para el ángulo (medido en radianes) que forma el diámetro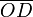 con la dirección horizontal OX. Se considera que el sistema parte de la posición inicial θ = 0. En el punto D hay conectada una cuerda flexible e inextensible de longitud L = πR que, cuando el disco gira, se va enrollando sobre su contorno, finalizando el proceso cuando θ = π. Además, un punto material pesado P hace que el tramo de cuerda no enrollado siempre penda verticalmente.

1. Obtenga la ecuación paramétrica de la trayectoria Γ.
2. El extremo D del diámetro realiza un movimiento circular uniforme, siendo su aceleración 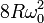. ¿Cómo es la correspondiente ley horaria para el ángulo θ?
3. Calcule la expresión de la componente intrínseca de la velocidad de la partícula P.
4. Aceleración tangencial del punto P.
5. Radio de curvatura de la trayectoria de P en el punto de inicial.

2.7 Cuestión sobre cinemática de la partícula

Una partícula se mueve con velocidad y aceleración instantáneas, 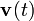y 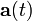, tales que su producto escalar tiene un valor k², constante en el tiempo, y su producto vectorial es un vector 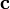, también constante. Considerando que el móvil parte del reposo, determine las siguientes magnitudes:

1. Ángulo que forman en cada instante las direcciones de la velocidad y la aceleración.
2. Ley horaria v(t) que verifica el módulo de la velocidad instantánea (celeridad).
3. Radio de curvatura de la trayectoria en función de la distancia s recorrida por la partícula, R_κ(s).

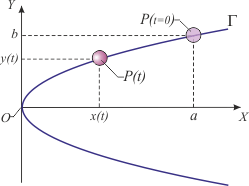
2.8 Punto moviéndose sobre una parábola

Un punto inicialmente en reposo en la posición x = a, y = b,

describe la parábola 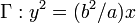. Se conoce la componente y de la aceleración: a_y = − k²y, con k = cte. Determina en función del tiempo la posición, velocidad y aceleración. ¿Cuál es la siguiente posición de reposo, y cuánto tiempo tarda en alcanzarla?

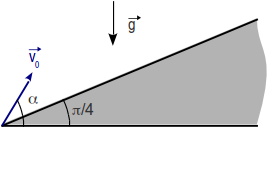
2.9 Tiro parabólico sobre un plano inclinado

Se tiene el plano inclinado de la figura que forma un ángulo π / 4 con la horizontal. se dispara una partícula desde el punto más bajo, con una velocidad inicial , de módulo v₀ y con un ángulo α con la horizontal.

1. Calcula la distancia entre el punto de partida y el de impacto sobre el plano inclinado, así como la velocidad (vector) con la que impacta.
2. Calcula el trabajo realizado por la fuerza gravitatoria a lo largo de la trayectoria de la partícula, así como la potencia que la fuerza gravitatoria transmite a la partícula en cada instante.
3. Para el caso α = π / 3, calcula las componentes intrínsecas de la aceleración en el punto de impacto y el radio de curvatura.

2.10 Partícula recorriendo una espiral

Una partícula recorre una espiral logarítmica con coordenadas polares 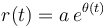, donde θ(t) = ωt, Aquí, t es el tiempo y a y ω son constantes. Encuentra la expresión del vector de posición en coordenadas polares y del triedro intrínseco en cada punto de la trayectoria en función del tiempo. Determina la ley horaria s(t) que da la distancia recorrida por la partícula en función del tiempo.

2.11 Partícula moviéndose sobre una parábola

Una partícula se mueve siguiendo la trayectoria descrita por la curva de ecuaciones implícitas y = A(1 − x² / A²) y z = 0, donde A es una constante. La coordenada x varía en el intervalo .

1. Determina el vector tangente en función de la posición de la partícula
2. Suponiendo que en t = 0 la distancia recorrida es s = 0 encuentra la expresión que da la distancia total recorrida sobre la curva.
3. ¿Cuál es el vector normal a la trayectoria en x = 0?

2.12 Partícula con curvatura y aceleración tangencial dependientes del tiempo

Una partícula se mueve de modo que, en todo instante, su curvatura es κ = At y su aceleración tangencial es a_T = Bt, siendo A y B constantes. Suponemos que en el instante inicial la partícula está en reposo.

1. ¿Cuáles son las unidades base de las constantes en el SI?
2. Suponiendo que en t = 0 se tiene s = 0, calcula la distancia recorrida en cada instante de tiempo
3. Calcula el módulo de la aceleración en cada instante.