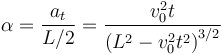Entrar Página Discusión Historial Go to the site toolbox

Barra con extremos sobre los ejes, Enero 2012 (G.I.C.)

De Laplace

Contenido

1 Enunciado

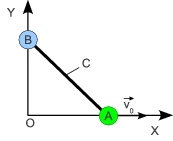
Dos partículas, A y B, de masa m, están unidas por una barra rígida de longitud L y masa despreciable. La partícula A se mueve sobre el eje OX con velocidad uniforme v0, mientras que la partícula B está obligada a moverse sobre el eje OY. Si en el instante t = 0 la partícula A se encontraba en el punto O

  1. Encuentra la posición, velocidad y aceleración de la partícula B en función de v0 y del tiempo.
  2. ¿Cuál es el vector de posición y la velocidad del punto medio de la barra (C) en función de v0 y t0?
  3. Describe la curva que corresponde a la trayectoria del punto medio de la barra.
  4. ¿Que tipo de movimiento describe el punto medio de la barra? Razona tu respuesta.


2 Solución

2.1 Extremo B

El vector de posición del extremo B de la barra puede calcularse a partir de la posición del extremo A y del vector 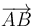\overrightarrow{AB}

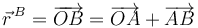
\vec{r}^{\,B} = \overrightarrow{OB} = \overrightarrow{OA} + \overrightarrow{AB}

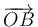El vector \overrightarrow{OB} es el vector de posición del punto A. El extremo A se mueve con velocidad de módulo v0 uniforme sobre el eje OX. Por tanto su velocidad es

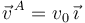
\vec{v}^{\,A} = v_0\,\vec{\imath}

Como en el instante inicial el punto A estaba en el origen de coordenadas, su vector de posición es

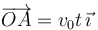
\overrightarrow{OA} = v_0t\,\vec{\imath}

El vector 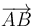\overrightarrow{AB} puede calcularse como

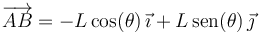
\overrightarrow{AB} = -L\cos(\theta)\,\vec{\imath} + L\,\mathrm{sen}(\theta)\,\vec{\jmath}

donde L es la longitud de la barra y θ es el ángulo de la figura. Tenemos

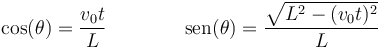
\cos(\theta) = \dfrac{v_0 t}{L} \qquad\qquad \mathrm{sen}(\theta) = \dfrac{\sqrt{L^2-(v_0t)^2}}{L}

Por tanto el vector 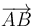\overrightarrow{AB} es

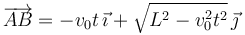
\overrightarrow{AB} = -v_0t\,\vec{\imath} + \sqrt{L^2-v_0^2t^2}\,\vec{\jmath}

Ahora podemos expresar el vector de posición del extremo B, y derivando sucesivamente respecto del tiempo, su velocidad y aceleración

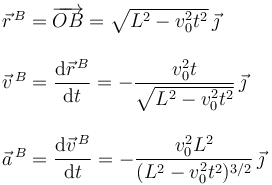
\begin{array}{l} \vec{r}^{\,B} = \overrightarrow{OB} = \sqrt{L^2-v_0^2t^2}\,\vec{\jmath}\\ \\ \vec{v}^{\,B} = \dfrac{\mathrm{d}\vec{r}^{\,B}}{\mathrm{d}t} =- \dfrac{v_0^2 t}{\sqrt{L^2-v_0^2t^2}}\,\vec{\jmath}\\ \\ \vec{a}^{\,B} = \dfrac{\mathrm{d}\vec{v}^{\,B}}{\mathrm{d}t} =- \dfrac{v_0^2 L^2}{(L^2-v_0^2t^2)^{3/2}}\,\vec{\jmath} \end{array}

2.2 Posición y velocidad del punto medio de la barra

Podemos proceder de forma similar al apartado anterior. El vector de posición del punto medio de la barra puede construirse como

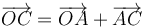
\overrightarrow{OC} = \overrightarrow{OA} + \overrightarrow{AC}

Como está en el punto medio, tenemos

\overrightarrow{AC} = \dfrac{1}{2}\overrightarrow{AB}

Entonces, el vector de posición del punto C y su velocidad son

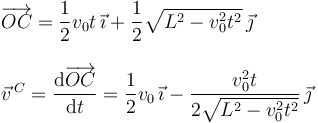
\begin{array}{l} \overrightarrow{OC} = \dfrac{1}{2}v_0t\,\vec{\imath} + \dfrac{1}{2}\sqrt{L^2-v_0^2t^2}\,\vec{\jmath}\\ \\ \vec{v}^{\,C} = \dfrac{\mathrm{d}\overrightarrow{OC}}{\mathrm{d}t}= \dfrac{1}{2}v_0\,\vec{\imath} - \dfrac{v_0^2t}{2\sqrt{L^2-v_0^2t^2}}\,\vec{\jmath} \end{array}

2.3 Curva que describe el punto medio de la barra

Las componentes cartesianas del vector \overrightarrow{OC} son

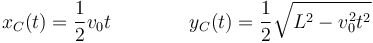
x_{C}(t) = \dfrac{1}{2}v_0t\qquad\qquad y_C(t) = \dfrac{1}{2}\sqrt{L^2-v_0^2t^2}

Elevando al cuadrado ambas componentes y sumándolas tenemos

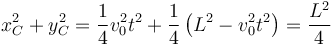
x_C^2 + y_C^2 = \dfrac{1}{4}v_0^2t^2 + \dfrac{1}{4}\left(L^2 - v_0^2t^2\right) = \dfrac{L^2}{4}

Esta expresión puede escribirse

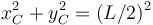
x_C^2 + y_C^2 = (L/2)^2

Esta es la ecuación de una circunferencia con centro en el punto O y radio L / 2.

2.4 Tipo de movimiento del punto C

Por lo visto en el apartado anterior el movimiento es circular. Para precisar más podemos fijarnos en el módulo de la velocidad del punto C. Tenemos

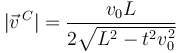
|\vec{v}^{\,C}| = \dfrac{v_0 L}{2\sqrt{L^2 - t^2v_0^2}}

La aceleración tangencial del punto C se puede calcular como

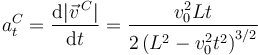
a_t^C = \dfrac{\mathrm{d}|\vec{v}^{\,C}|}{\mathrm{d}t} = \dfrac{v_0^2L t}{2\left(L^2-v_0^2t^2\right)^{3/2}}

En el movimiento circular la aceleración tangencial puede calcularse como

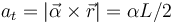
a_t = |\vec{\alpha}\times\vec{r}| = \alpha L/2

Por tanto, el movimiento es circular con aceleración angular

\alpha = \dfrac{a_t}{L/2} = \dfrac{v_0^2 t}{\left(L^2-v_0^2t^2\right)^{3/2}}

Obtenido de "http://tesla.us.es/wiki/index.php/Barra_con_extremos_sobre_los_ejes,_Enero_2012_(G.I.C.)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 22:22, 18 nov 2012. - Esta página ha sido visitada 3.268 veces. - Aviso legal - Acerca de Laplace