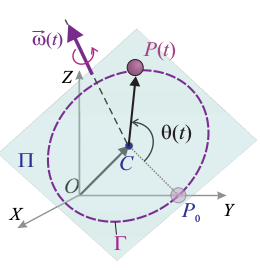
F1 GIA PPC 2013, Punto moviéndose en una circunferencia sobre un plano
De Laplace
Contenido |
1 Enunciado
Un punto material P se mueve recorriendo la circunferencia Γ contenida en un plano fijo Π y cuyo centro es el punto C, dado por el segmento orientado 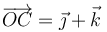 , cuyas componentes se miden en metros (m) y están referidas a un sistema cartesiano OXYZ. En el instante inicial (t = 0), el punto móvil P ocupa la posición determinada por el segmento orientado
, cuyas componentes se miden en metros (m) y están referidas a un sistema cartesiano OXYZ. En el instante inicial (t = 0), el punto móvil P ocupa la posición determinada por el segmento orientado 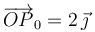 . A partir de ́esta, la partícula realiza un movimiento circular caracterizado por un vector rotación instantánea o velocidad angular, cuyas componentes
medidas en radianes por segundo son:
. A partir de ́esta, la partícula realiza un movimiento circular caracterizado por un vector rotación instantánea o velocidad angular, cuyas componentes
medidas en radianes por segundo son:
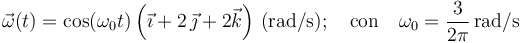
El movimiento se verifica en el intervalo de tiempo 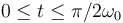 , de manera que la partícula recorre la circunferencia una sola vez, y siempre en sentido antihorario.
, de manera que la partícula recorre la circunferencia una sola vez, y siempre en sentido antihorario.
- ¿Cómo es la ley horaria θ(t) que describe el ́angulo recorrido por el segmento orientado
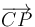 , desde el instante inicial hasta el instante t?
, desde el instante inicial hasta el instante t?
- ¿Cómo es el vector binormal del triedro intrínseco a la trayectoria, en función de la posición de la partícula?
- ¿Cómo es la curvatura de la trayectoria durante el movimiento?
- ¿Cómo es la velocidad instantánea de la partícula en t = 0?
- Calcule las componentes tangencial y normal de la velocidad en el instante inicial
1.1 Ley horaria para bθ
El vector rotación se define como

El vector 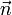 se obtiene dividiendo
se obtiene dividiendo 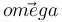 por su módulo
por su módulo

Por tanto
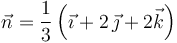
Comparando  y
y 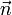 vemos que
vemos que

Por tanto

Esta es una ecuación diferencial que podemos integrar.
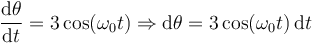
Integramos en los dos lados e incorporamos en los límites la condición inicial θ(0) = 0, pues 

Sustituyendo el valor de ω0 obtenemos

1.2 Vector binormal
Como la trayectoria es una circunferencia plana el vector binormal es siempre el mismo, y coincide con el vector 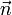 calculado antes
calculado antes

1.3 Curvatura de la trayectoria
Al ser una circunferencia, la curvatura es constante e igual a la inversa del radio de la circunferencia

El radio es el módulo del vector 

Por tanto

1.4 Velocidad en el instante inicial
Podemos calcular la velocidad a partir de vector rotación y del vector de posición respecto del centro de la circunferencia

1.5 Componentes intrínsecas de la aceleración en el instante inicial
La aceleración normal es

Para la aceleración tangencial tenemos

Aquí  es la aceleración angular.
es la aceleración angular.