Cuestión de cinemática del punto, Noviembre 2012 (F1 GIA)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

Una partícula $P$ se mueve respecto de un sistema de referencia cartesiano $O X Y Z$ de manera que en un cierto instante $t 0$ , su velocidad $\vec{v}$ y su aceleración $\vec{a}$ están descritas por los vectores

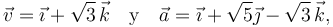
$\vec{v}=\vec{\imath}+\sqrt{3}\!\ \vec{k}\quad\mathrm{y}\quad\vec{a}=\vec{\imath}+\sqrt{5}\vec{\jmath}-\sqrt{3}\!\ \vec{k}\mathrm{,}$

con sus componentes medidas en $m / s$ y $m / s 2$ ,respectivamente. Determine, en el instante considerado, las siguientes magnitudes cinemáticas:

Módulo de la velocidad (celeridad) y su derivada.
Componente normal de la aceleración y radio de curvatura de la trayectoria.
Vector aceleración normal.
Triedro intrínseco.
La localización del centro de curvatura si en ese instante la partícula se halla en el origen.

2 Solución

En el instante

t 0

, cuando la

partícula ocupa la posición $P (t 0)$ , su velocidad y aceleración instantánea son sendos vectores de coordenadas conocidad en un determinado sistema de referencia cartesiano $O X Y Z$ . Sin embargo, se quieren determinar sus componentes en el triedro intrínseco; es decir, el formado por las direcciones tangente $\vec{T}$ , normal $\vec{N}$ y binormal $\vec{B}$ a la trayectoria en el punto $P (t 0)$ :

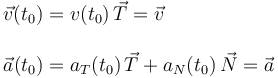
$\begin{array}{l} \displaystyle \vec{v}(t_0)=v(t_0)\!\ \vec{T}=\vec{v}\\ \\ \displaystyle \vec{a}(t_0)=a_T(t_0)\!\ \vec{T}+a_N(t_0)\!\ \vec{N}=\vec{a}\end{array}$

2.1 Celeridad y su derivada

Al tomar como sentido del vector tangente en $P (t 0)$ el sentido de movimiento de la partícula en dicho instante, se tendrá que la celeridad $v (t 0)$ coincide con el módulo del vector velocidad instantánea en $t 0$ , pues el vector tangente es, por defininición un vector unitario. En consecuencia, la magnitud $v (t 0)$ puede determinarse fácilmente a partir de las coordenas cartesianas de la velocidad:

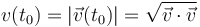
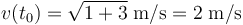
$v(t_0)=|\vec{v}(t_0)|=\sqrt{\vec{v}\cdot\vec{v}}$ $\Rightarrow$ $v(t_0)=\sqrt{1+3}\;\mathrm{m}/\mathrm{s}=2\;\mathrm{m}/\mathrm{s}$

Y además podemos conocer cómo es el cambio que por unidad de tiempo está experimentando la celeridad en el instante $t 0$ , si determinamos la componente tangencial de la aceleración instantánea en dicho instante. Esto lo podemos hacer evaluando el producto escalar de los vectores velocidad y aceleración instantánea:

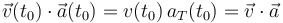
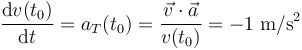
$\vec{v}(t_0)\cdot\vec{a}(t_0)=v(t_0)\!\ a_T(t_0)=\vec{v}\cdot\vec{a}$ $\Rightarrow$ $\frac{\mathrm{d}v(t_0)}{\mathrm{d}t}=a_T(t_0)=\frac{\vec{v}\cdot\vec{a}}{v(t_0)}=-1\;\mathrm{m}/\mathrm{s}^2$

Obsérvese que el hecho de que la aceleración tangencial instantánea sea negativa y, por consiguiente, la celeridad disminuya, va a estar directamente relacionada con que los vectores $\vec{v}$ y $\vec{a}$ formen un ángulo mayor que $π / 2$ , de manera que su producto escalar es negativo.

2.2 Componente normal de la aceleración y radio de curvatura

La componente normal de la aceleración instantánea, $a N (t 0)$ , la calculamos a partir del módulo del producto vectorial de los vectores velocidad y aceleración. Recuérdese que esta magnitud es siempre positiva o nula, y que el triedro instrínseco está constituido por tres vectores unitarios, de manera que...

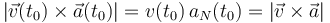
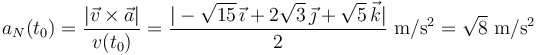
$|\vec{v}(t_0)\times\vec{a}(t_0)|=v(t_0)\!\ a_N(t_0)=|\vec{v}\times\vec{a}|$ $\Rightarrow$ $a_N(t_0)=\frac{|\vec{v}\times\vec{a}|}{v(t_0)}=\frac{|-\sqrt{15}\!\ \vec{\imath}+2\sqrt{3}\!\ \vec{\jmath}+\sqrt{5}\!\ \vec{k}|}{2}\;\mathrm{m}/\mathrm{s}^2=\sqrt{8}\;\mathrm{m}/\mathrm{s}^2$

Por otra parte, el radio de curvatura $R κ (P)$ de la trayectoria seguida por la partícula, en el punto $P$ que ésta ocupa en el instante $t 0$ es igual a la relación entre el cuadrado de la celeridad y la componente normal de la aceleración:

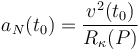
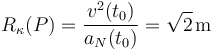
$a_N(t_0)=\frac{v^2(t_0)}{R_\kappa(P)}$ $\Rightarrow$ $R_\kappa(P)=\frac{v^2(t_0)}{a_N(t_0)}=\sqrt{2}\!\ \mathrm{m}$

La curvatura es

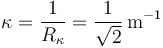
$\kappa = \dfrac{1}{R_{\kappa}} = \dfrac{1}{\sqrt{2}}\,\mathrm{m^{-1}}$

2.3 Aceleración normal

La aceleración normal de la partícula en el instante bajo estudio es el vector cuyo módulo es la componente $a N (t 0)$ de la aceleración y tiene la dirección y el sentido del vector unitario normal a la trayectoria en el punto ocupado por la partícula en dicho instante. El módulo de este vector lo acabamos de calcular y faltaría por determinar el vector normal a la trayectoria. Este vector es igual al producto vectorial de los vectores binormal y tangente. El primero de ellos es un vector unitario con la dirección y el sentido del producto vectorial de la velocidad por la aceleración; el segundo es el unitario en la dirección y el sentido de la velocidad:

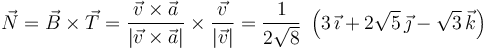
$\vec{N}=\vec{B}\times\vec{T}=\frac{\vec{v}\times\vec{a}}{|\vec{v}\times\vec{a}|}\times\frac{\vec{v}}{|\vec{v}|}=\frac{1}{2\sqrt{8}}\ \left(3\!\ \vec{\imath}+2\sqrt{5}\!\ \vec{\jmath}-\sqrt{3}\!\ \vec{k}\right)$

Se tendría, por tanto,

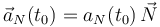
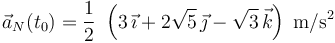
$\vec{a}_N(t_0)=a_N(t_0)\!\ \vec{N}$ $\Rightarrow$ $\vec{a}_N(t_0)=\frac{1}{2}\ \left(3\!\ \vec{\imath}+2\sqrt{5}\!\ \vec{\jmath}-\sqrt{3}\!\ \vec{k}\right)\;\mathrm{m}/\mathrm{s}^2$

Otra posible forma de determinar la aceleración normal es restando al vector aceleración instantánea la compomente tangencial multiplicada por el vector tangente a la trayectoria en el punto considerado. El vector tangente es

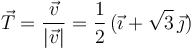
$\vec{T} = \dfrac{\vec{v}}{|\vec{v}|} = \dfrac{1}{2}\,(\vec{\imath} + \sqrt{3}\,\vec{\jmath})$

La aceleración tangencial es

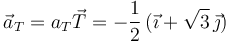
$\vec{a}_T = a_T\vec{T} = -\dfrac{1}{2}\,(\vec{\imath} + \sqrt{3}\,\vec{\jmath})$

Es decir,

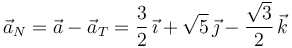
$\vec{a}_N=\vec{a}-\vec{a}_T= \dfrac{3}{2}\,\vec{\imath} + \sqrt{5}\,\vec{\jmath}-\dfrac{\sqrt{3}}{2}\,\vec{k}$

2.4 Triedro intrínseco

El vector normal es

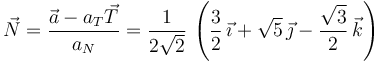
$\vec{N} = \dfrac{\vec{a}-a_T\vec{T}}{a_N} = \dfrac{1}{2\sqrt{2}}\,\left(\dfrac{3}{2}\,\vec{\imath} + \sqrt{5}\,\vec{\jmath} - \dfrac{\sqrt{3}}{2}\,\vec{k}\right)$

El vector binormal puede calcularse de dos formas

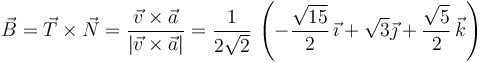
$\vec{B} = \vec{T}\times\vec{N} = \dfrac{\vec{v}\times\vec{a}}{|\vec{v}\times\vec{a}|}= \dfrac{1}{2\sqrt{2}}\,\left( -\dfrac{\sqrt{15}}{2}\,\vec{\imath} + \sqrt{3}\vec{\jmath} + \dfrac{\sqrt{5}}{2}\,\vec{k} \right)$

El triedro intrínseco lo forman

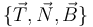
$\{\vec{T}, \vec{N}, \vec{B}\}$

2.5 Centro de curvatura

Si la partícula está en el origen el vector de posición del centro de curvatura es

$\vec{r}_{\kappa} = R_{\kappa}\vec{N} = \dfrac{1}{4}\, (3\,\vec{\imath} +2\sqrt{5}\,\vec{\jmath} - \sqrt{3}\,\vec{k})$

Cuestión de cinemática del punto, Noviembre 2012 (F1 GIA)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Celeridad y su derivada

2.2 Componente normal de la aceleración y radio de curvatura

2.3 Aceleración normal

2.4 Triedro intrínseco

2.5 Centro de curvatura

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES