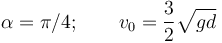F1 GIA PPC 2013, Cañon lanzando partícula sobre un carrito deslizando sobre plano inclinado
De Laplace
Contenido |
1 Enunciado
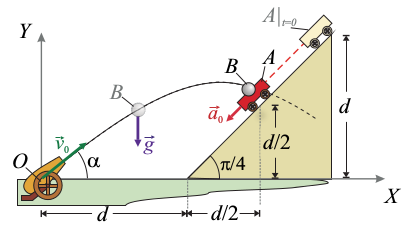
Un móvil A, que puede ser considerado como un cuerpo puntual, se desplaza por una ladera con una pendiente de 45o respecto de la horizontal. El móvil desciende por la ladera realizando un movimiento rectilíneo uniformemente acelerado, siendo el módulo de su aceleración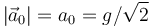 
. En el instante de iniciar el descenso el móvil se encuentra en reposo, a una altura d. Además, a una distancia d de la base de la ladera, en dirección horizontal, se halla emplazado un dispositivo lanzador de proyectiles a los que imprime una velocidad inicial de módulo v0 y formando un ángulo α con la horizontal.
- Encuentre la expresión de las ecuaciones horarias que describen el movimiento del móvil A respecto al sistema de referencia del dibujo.
- En el instante en el que el móvil A inicia el descenso, el lanzado dispara un proyectil B que, a partir de entonces, se mueve con la aceleración debida a la acción de la gravedad,
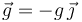, constante en módulo, dirección y sentido. ¿Qué valores deben tener el ángulo de lanzamiento α y la celeridad inicial v0 del proyectil B para que éste impacte sobre el móvil A cuando se encuentra en la mitad de la ladera?
2 Solución
2.1 Movimiento de A
La partícula A se mueve con un movimiento uniformemente acelerado con aceleración
La posición inicial de la partícula es
y su velocidad inicial es cero.
Podemos tratar de manera separada el movimiento en las dos componentes, y aplicar en cada una de ellas las fórmulas de movimiento uniformemente acelerado
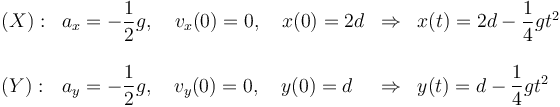
Por tanto, el vector de posición del móvil A en cualquier instante es
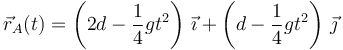
2.2 Parámetros para la partícula B
La partícula B realiza un movimiento parabólico en el campo gravitatorio terrestre. Parte del origen y su velocidad inicial es
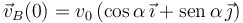
El movimiento horizontal es uniforme y el vertical uniformemente acelerado con aceleración − g. La posición de B en cada instante es
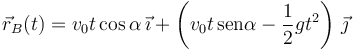
Queremos que se encuentre con A en el punto medio de la ladera. En ese instante de tiempo, tc, la posición de A debe cumplir
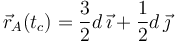
Por otro lado, usando las ecuaciones horarias para A tenemos
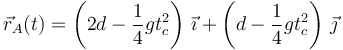
Igualando las componentes de estos dos vectores obtenemos el valor de tc
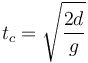
Queremos que en ese instante B también esté en el mismo punto, es decir
Podemos resolver estas ecuaciones pasando el término en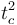 
de la segunda a la derecha y dividiéndolas. Así obtenemos el valor de α. Después despejamos v0
