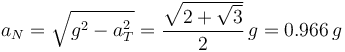Tiro parabólico sobre un plano inclinado, Diciembre 2012 (G.I.C.)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

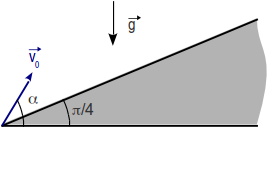
Se tiene el plano inclinado de la figura que forma un ángulo $π / 4$ con la horizontal. se dispara una partícula desde el punto más bajo, con una velocidad inicial $\vec{v}_0$ , de módulo $v 0$ y con un ángulo $α$ con la horizontal.

Calcula la distancia entre el punto de partida y el de impacto sobre el plano inclinado, así como la velocidad (vector) con la que impacta.
Calcula el trabajo realizado por la fuerza gravitatoria a lo largo de la trayectoria de la partícula, así como la potencia que la fuerza gravitatoria transmite a la partícula en cada instante.
Para el caso $α = π / 3$ , calcula las componentes intrínsecas de la aceleración en el punto de impacto y el radio de curvatura.

2 Solución

2.1 Punto de impacto sobre el plano inclinado

Antes de chocar con el plano inclinado el movimiento de la partícula es un tiro parabólico. El plano no interfiere con este movimiento. Vamos a describir el movimiento antes de que impacte en el plano.

Escogemos el eje $X$ horizontal al suelo y el eje $Y$ perpendicular, coincidiendo con la dirección de la gravedad. En esos ejes la aceleración de la partícula es

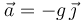
$\vec{a} = -g\,\vec{\jmath}$

Obtenemos la velocidad integrando la ecuación diferencial correspondiente

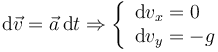
$\mathrm{d}\vec{v} = \vec{a}\,\mathrm{d}t \Rightarrow \left\{ \begin{array}{lcl} \mathrm{d}v_x = 0\\ \mathrm{d}v_y = -g \end{array} \right.$

La primera ecuación nos dice que la componente horizontal de la velocidad es constante, mientras que la segunda implica que el movimiento vertical es un movimiento uniformemente acelerado. La velocidad inicial es

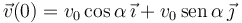
$\vec{v}(0) = v_0\cos\alpha\,\vec{\imath} + v_0\,\mathrm{sen}\,\alpha\,\vec{\jmath}$

Entonces la velocidad en cada instante es

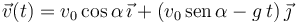
$\vec{v}(t) = v_0\cos\alpha\,\vec{\imath} + (v_0\,\mathrm{sen}\,\alpha -g\,t)\,\vec{\jmath}$

Integrando otra vez, y colocando el origen de coordenadas en el punto de partida tenemos

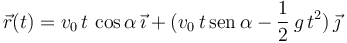
$\vec{r}(t) = v_0\,t\,\cos\alpha\,\vec{\imath} + (v_0\,t\,\mathrm{sen}\,\alpha - \dfrac{1}{2}\,g\,t^2)\,\vec{\jmath}$

Cuando la partícula impacta con el plano el ángulo que forma el vector de posición con el eje $X$ es $π / 4$ . Eso es equivalente a decir que las componentes en ambos ejes son iguales. A partir de ahí obtenemos el instante de tiempo para el que impacta con el plano

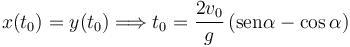
$x(t_0) = y(t_0) \Longrightarrow t_0 = \dfrac{2v_0}{g}\,(\mathrm{sen}\alpha-\cos\alpha)$

La distancia del origen al punto de impacto es

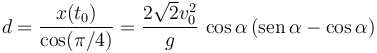
$d = \dfrac{x(t_0)}{\cos(\pi/4)} = \dfrac{2\sqrt{2}v_0^2}{g}\,\cos\alpha\,(\mathrm{sen}\,\alpha-\cos\alpha)$

La velocidad en el momento del impacto se obtiene sustituyendo el valor de $t 0$ en la expresión de la velocidad

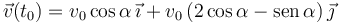
$\vec{v}(t_0) = v_0\cos\alpha\,\vec{\imath} + v_0\,(2\cos\alpha -\mathrm{sen}\,\alpha)\,\vec{\jmath}$

2.2 Trabajo realizado por la fuerza gravitatoria

Por definición, el trabajo realizado por la fuerza gravitatoria es igual a la variación de energía potencial gravitatoria cambiada de signo

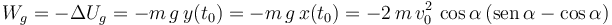
$W_g = -\Delta U_g = -m\,g\,y(t_0) = -m\,g\,x(t_0) = -2\,m\,v_0^2\,\cos\alpha\,(\mathrm{sen}\,\alpha-\cos\alpha)$

En cada instante, la potencia de la fuerza gravitatoria sobre la partícula es

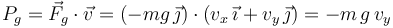
$P_g = \vec{F}_g\cdot\vec{v} = (-mg\,\vec{\jmath})\cdot(v_x\,\vec{\imath} + v_y\,\vec{\jmath}) = -m\,g\,v_y$

Sustituyendo la expresión de la componente de la velocidad tenemos

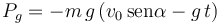
$P_g = -m\,g\,(v_0\,\mathrm{sen}\alpha - g\,t)$

2.3 Componentes intrínsecas de la aceleración en el punto de impacto

Si $α = π / 3$ la velocidad en el punto de impacto es

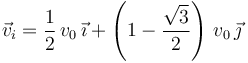
$\vec{v}_i = \dfrac{1}{2}\,v_0\,\vec{\imath} + \left(1-\dfrac{\sqrt{3}}{2}\right)\,v_0\,\vec{\jmath}$

La aceleración es la misma siempre

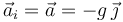
$\vec{a}_i = \vec{a} = -g\,\vec{\jmath}$

La componente tangencial es

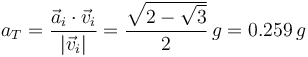
$a_T = \dfrac{\vec{a}_i\cdot\vec{v}_i}{|\vec{v}_i|} = \dfrac{\sqrt{2-\sqrt{3}}}{2}\,g = 0.259\,g$

La componente normal es

$a_N = \sqrt{g^2-a_T^2} = \dfrac{\sqrt{2+\sqrt{3}}}{2}\,g = 0.966\,g$

Tiro parabólico sobre un plano inclinado, Diciembre 2012 (G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Punto de impacto sobre el plano inclinado

2.2 Trabajo realizado por la fuerza gravitatoria

2.3 Componentes intrínsecas de la aceleración en el punto de impacto

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES