Movimiento oscilatorio armónico unidimensional
De Laplace
1 Enunciado
Un punto inicialmente en reposo en la posición x = L describe un movimiento rectilíneo sobre el eje OX, de modo que su aceleración es de la forma a = − k2x. Determina en función del tiempo su posición y velocidad. ¿Cuál es la siguiente posición de reposo, y cuánto tiempo tarda en alcanzarla?
2 Solución
Al ser el movimiento unidimensional sobre el eje OX podemos describir los vectores cinemáticos de la partícula como
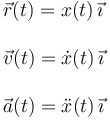
De nuevo, como el movimiento es unidimensional, prescindiremos de los vectores a partir de ahora.
El enunciado nos da una relación entre la aceleración y la posición. Teniendo en cuenta que 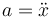 nos queda
nos queda
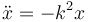
Esta es una ecuación diferencial en la que la incógnita es la función x(t). Esta ecuación en concreto es la ecuación diferencial del oscilador armónico. Se reconoce por su estructura. A la izquierda está la derivada segunda de la función incógnita, y a la derecha la propia función incógnita, multiplicada por un numero positivo (k2) y con un signo menos.
Hay dos funciones que son solución de esta ecuación: cos(kt) y 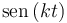 . Podemos verificarlo haciendo las derivadas
. Podemos verificarlo haciendo las derivadas
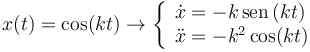
Y por tanto se verifica la ecuación. Si derivamos el seno ocurre lo mismo.
Si tenemos dos posibles soluciones, ¿cual es la buena?. Pues una combinación lineal de las dos. La ecuación diferencial es lineal, que quiere decir que la función incógnita y sus derivadas sólo aparecen como potencias de exponente 1. En este tipo de ecuaciones una combinación lineal de soluciones también es solución de la ecuación. Entonces, la solución mas general se puede escribir así
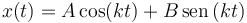
Podemos verificar de nuevo que esta expresión es solución de la ecuación diferencial
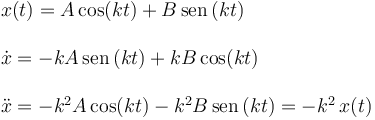
A y B son constantes de integración. Su valor se determina a partir de las condiciones iniciales, es decir, la posición y velocidad iniciales de la partícula. El enunciado nos dice que parte del reposo y a una distancia L del origen. Es decir, las condiciones iniciales son

Con estas condiciones obtenemos dos ecuaciones para A y B
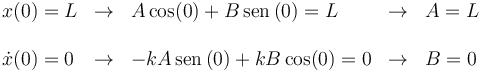
Por tanto la posición y la velocidad de la partícula en cada instante vienen dadas por
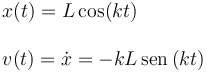
La partícula realiza un movimiento oscilatorio entre los puntos x = L y x = − L. El tiempo que tarda en ir y volver es el período. Para obtener su valor imponemos que el coseno realice un ciclo completo
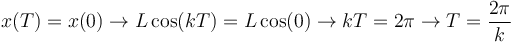
Los puntos de reposo son aquellos en que la velocidad es nula, es decir
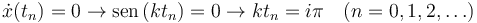
Es decir los instantes en que la partícula está en reposo son
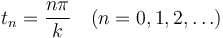
Señalemos que el intervalo de tiempo entre dos paradas es
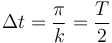
Corresponden a las posiciones x = L y x = − L.





