Barra deslizando sobre una circunferencia (G.I.A.)

De Laplace

Contenido

1 Enunciado
2 Solución
- 2.1 Ecuaciones horarias
- 2.2 Aceleración tangencial y normal

1 Enunciado

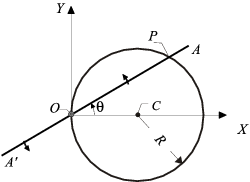
En un plano $O X Y$ , se define el sistema cinemático formado por los dos siguientes elementos geométricos:

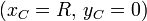una circunferencia fija, de radio $R$ y centrada en el punto $C$ de coordenadas $(x_C=R,\, y_C=0)$ ;
un segmento rectilíneo móvil $A' A$ , de longitud superior a $4 R$ , el cual gira con velocidad angular constante $ω$ (en sentido antihorario) alrededor de un eje fijo que pasa por su punto medio $O$ y es normal al plano $O X Y$ (eje $O Z$ ).

Sabiendo que el ángulo $θ$ ( que forman $O A$ y $O X$ ) es nulo en el instante inicial $(t = 0)$ ; y considerando como móvil problema el punto $P$ en el que se cortan el segmento $A' A$ y la circunferencia , se pide:

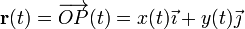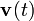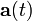item Determinar las ecuaciones horarias, $\mathbf{r}(t) = \overrightarrow{OP}(t) = x(t)\vec{\imath}+y(t)\vec{\jmath}$ , del punto $P$ , así como sus vectores velocidad, $\mathbf{v}(t)$ , y aceleración, $\mathbf{a}(t)$ .
Calcular las aceleraciones tangencial y normal de dicho punto $P$ .

2 Solución

2.1 Ecuaciones horarias

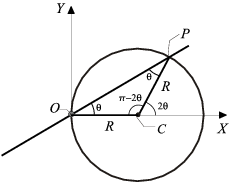
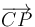Determinamos la posición del punto $P$ a través de los vectores $\overrightarrow{OC}$ y $\overrightarrow{CP}$ ,

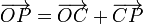
$\overrightarrow{OP} = \overrightarrow{OC} + \overrightarrow{CP}$

El vector $\overrightarrow{OC}$ es

$\overrightarrow{OC} = R\,\vec{\imath} = [\,R\,,\,0\,,\,0\,];$

En el dibujo vemos que el ángulo que forma el vector 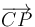$\overrightarrow{CP}$ con el eje $O X$ es $2θ$ . Como su módulo es el radio $R$ tenemos

$\overrightarrow{CP} = R\,\cos(2\theta)\,\vec{\imath} + R\,\,\mathrm{sen}\,(2\theta)\,\vec{\jmath} = [\,R\,\cos(2\theta)\,,\,R\,\,\mathrm{sen}\,(2\theta)\,,0\,]$

Así pues la posición del punto $P$ viene dada por el vector

$\overrightarrow{OP} = [\,R\,(1+\cos(2\theta))\,,\,R\,\,\mathrm{sen}\,(2\theta)\,,\,0\,]$

Teniendo en cuenta que $θ(t) = ω t$ tenemos 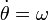$\dot{\theta}=\omega$ y por tanto

$\begin{array}{l} \vec{v}_P = \dot{\overrightarrow{OP}} = [\,-2R\omega\,\mathrm{sen}\,(2\theta)\,,\,2R\omega\cos(2\theta)\,,\,0\,] \\ \\ \vec{a}_P = \dot{\vec{v}}_P = -4R\omega^2\,[\,\cos(2\theta)\,,\,\,\mathrm{sen}\,(2\theta)\,,\,0\,] \end{array}$