Comportamiento dieléctrico de la materia

De Laplace

Contenido

1 Introducción
2 Polarización
3 El vector desplazamiento D
4 Dieléctricos lineales y permitividad
5 Energía eléctrica en presencia de dieléctricos
6 Condensadores con dieléctricos
7 Problemas

1 Introducción

Todos los materiales permiten, en mayor o menor medida, el movimiento de cargas en su interior. Si se le aplica un campo eléctrico a un trozo de material tarde o temprano se llega al equilibrio electrostático. El periodo típico en que esto ocurre se denomina tiempo de relajación. Dependiendo de la duración del tiempo de relajación, los materiales pueden ordenarse, yendo desde los conductores muy buenos, como el cobre o la plata, con un tiempo de relajación muy corto (que se modelan como conductores perfectos hasta los que requieren periodos muy largos para alcanzar el equilibrio, como diversos plásticos o materiales orgánicos.

Para estos últimos materiales se emplea un modelo llamado dieléctrico ideal, que se caracteriza por no permitir en absoluto en flujo de carga por su interior. En este capítulo se consideran las propiedades de estos materiales. En el tema de corrientes eléctricas se estudia el comportamiento de dieléctricos no ideales.

2 Polarización

Artículo completo: Polarización de un medio material

Los dieléctricos ideales afectan a los campos eléctricos porque aunque no fluyen y se redistribuyan las cargas en su interior, las moléculas y átomos que lo componen se polarizan, bien por la formación de dipolos inducidos, bien por la orientación de dipolos permanentes. Se define la polarización del material como la densidad de momento dipolar

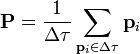
$\mathbf{P} = \frac{1}{\Delta\tau} \sum_{\mathbf{p}_i\in\Delta\tau} \mathbf{p}_i$

El potencial eléctrico debido a una polarización es la suma de los potenciales debidos a cada dipolo

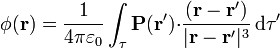
$\phi(\mathbf{r}) =\frac{1}{4\pi\varepsilon_0}\int_\tau \mathbf{P}(\mathbf{r}'){\cdot}\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\,\mathrm{d}\tau'$

Esta integral suele ser difícil de calcular por métodos analíticos.

Una descripción alternativa es mediante las densidades de carga de polarización o de carga ligada, definidas como

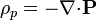
$\rho_p = -\nabla{\cdot}\mathbf{P}$ $\sigma_p = -\mathbf{n}{\cdot}[\mathbf{P}]\,$

La última fórmula, con el salto en la polarización, se aplica a una interfaz entre dos dieléctricos. Si uno de ellos es el vacío (en el cual 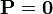$\mathbf{P}=\mathbf{0}$ ), esta expresión se reduce a 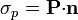$\sigma_p = \mathbf{P}{\cdot}\mathbf{n}$ . En términos de $ρ p$ y $σ p$ el potencial es

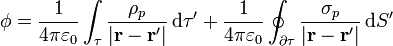
$\phi = \frac{1}{4\pi\varepsilon_0}\int_\tau\frac{\rho_p}{|\mathbf{r}-\mathbf{r}'|}\,\mathrm{d}\tau'+ \frac{1}{4\pi\varepsilon_0}\oint_{\partial\tau}\frac{\sigma_p}{|\mathbf{r}-\mathbf{r}'|}\,\mathrm{d}S'$

Empleando las densidades de cargas de polarización, las ecuaciones de la electrostática en presencia de dieléctricos se escriben como

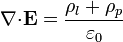
$\nabla{\cdot}\mathbf{E} = \frac{\rho_l+\rho_p}{\varepsilon_0}$ $\nabla\times \mathbf{E} =\mathbf{0}$

con las condiciones de salto

$\mathbf{n}{\cdot}[\mathbf{E}] = \frac{\sigma_l+\sigma_p}{\varepsilon_0}$ $\mathbf{n}\times [\mathbf{E}]=\mathbf{0}$

siendo $ρ l$ y $σ l$ las densidades de carga libre, definidas como aquellas que no son de polarización.

3 El vector desplazamiento D

Artículo completo: Vector desplazamiento

Las ecuaciones de la electrostática pueden simplifcarse definiendo el vector desplazamiento eléctrico

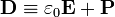
$\mathbf{D} \equiv \varepsilon_0 \mathbf{E} + \mathbf{P}$

de forma que las ecuaciones de la electrostática se transforman en

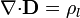
$\nabla{\cdot}\mathbf{D} = \rho_l$ $\nabla\times\mathbf{E} = \mathbf{0}$

con las condiciones de salto

$\mathbf{n}{\cdot}[\mathbf{D}] = \sigma_l$ $\mathbf{n}\times[\mathbf{E}]=\mathbf{0}$

La introducción del vector desplazamiento no significa la eliminación de la polarización de las ecuaciones, ya que el nuevo sistema de ecuaciones no es completo, ya que tenemos la divergencia de un campo y el rotacional de otro.

Para cerrar este sistema necesitamos dar explícitamente como depende la polarización del campo eléctrico (o dar el desplazamiento como función del campo). Esto es lo que se conoce como una relación constitutiva, que será dependiente de cada material.

4 Dieléctricos lineales y permitividad

Artículo completo: Dieléctrico lineal

El caso particular de relación constitutiva más frecuente e importante es el de los dieléctricos lineales}, en los cuales la polarización es proporcional al campo aplicado

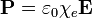
$\mathbf{P} = \varepsilon_0 \chi_e \mathbf{E}$

siendo $χ e$ la susceptibilidad del dieléctrico. De esta relación lineal se deduce que también $\mathbf{D}$ y $\mathbf{E}$ son proporcionales

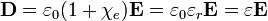
$\mathbf{D} = \varepsilon_0(1+\chi_e)\mathbf{E} = \varepsilon_0 \varepsilon_r\mathbf{E} = \varepsilon\mathbf{E}\,$

denominándose a 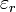$\varepsilon_r$ $ y $\varepsilon$ las permitividades relativa (adimensional) y absoluta (con las dimensiones de la permitividad del vacío) del dieléctrico. La permitividad relativa es un número mayor que la unidad, ya que los dipolos se alinean con el campo eléctrico.

Algunas permitividades de materiales, para campos estáticos, son

Permitividad relativa
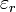
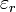
Material	$\varepsilon_r$	Material	$\varepsilon_r$
Agua	81	Aire	1.00054
Cuarzo	5.0	Argón	1.0052
Goma	3.0−4.0	Helio	1.000065
Mica	4.5−8.0	Neón	1.000123
Metacrilato	2.6−3.5	Oxígeno	1.00050

Hay que señalar que el agua no es en absoluto un dieléctrico ideal, por lo que el estudio de los campos en agua requiere necesariamente incluir los efectos de su conductividad.

La tabla anterior se refiere a la permitividad electrostática. Cuando tenemos campos variables en el tiempo (como una onda electromagnética que atraviesa un dieléctrico), la permitividad tiene un valor diferente, dependiente de la frecuencia del campo aplicado. A este efecto de dependencia con la frecuencia se denomina dispersión.Así, por ejemplo, para el agua, en el espectro visible, la permitividad relativa es 1.88, muy lejos del 81 estático.

Una partícula dieléctrica lineal en un campo externo adquiere un momento dipolar proporcional al campo aplicado y experimenta una fuerza que la empuja hacia donde el campo es más intenso

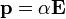
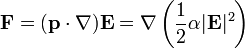
$\mathbf{p} = \alpha\mathbf{E}$ $\Rightarrow$ $\mathbf{F}=(\mathbf{p}\cdot\nabla)\mathbf{E}=\nabla\left(\frac{1}{2}\alpha|\mathbf{E}|^2\right)$

5 Energía eléctrica en presencia de dieléctricos

No existe expresión general para la energía almacenada en un sistema que incluye dieléctricos.

El valor de esta energía puede calcularse si se conoce el camino que han seguido los dieléctricos para polarizarse, esto es, si el valor del desplazamiento eléctrico en un punto ha pasado de 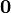$\mathbf{0}$ a $\mathbf{D}$ , la densidad de energía en dicho punto y la energía total pueden calcularse como

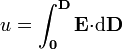
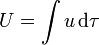
$u = \int_\mathbf{0}^\mathbf{D} \mathbf{E}{\cdot}\mathrm{d}\mathbf{D}$ $U = \int u\,\mathrm{d}\tau$

donde la primera integral representa la suma de los incrementos graduales de la densidad de energía a medida que aumenta el campo eléctrico.

Dado que estas integrales dependen no sólo del estado final, sino también de los pasos intermedios, se dice que los dieléctricos, en general, presentan histéresis.

En el caso particular importante de los dieléctricos lineales, la expresión anterior puede integrarse, obteniéndose una fórmula análoga a la del vacío

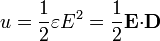
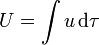
$u = \frac{1}{2}\varepsilon E^2=\frac{1}{2}\mathbf{E}{\cdot}\mathbf{D}$ $U = \int u\,\mathrm{d}\tau$

La energía resultante incluye tanto el trabajo para reunir las cargas libres como el necesario para polarizar el dieléctrico.

6 Condensadores con dieléctricos

Muchas de las propiedades de los sistemas de conductores en equilibrio en el vacío son extensibles al caso de que entre los conductores haya dieléctricos lineales. Así, la capacidad de un condensador relleno de dieléctrico se define como

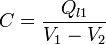
$C = \frac{Q_{l1}}{V_1-V_2}$

siendo $Q l 1$ la carga libre depositada en la superficie “1” del condensador.

Como consecuencia de que la permitividad relativa de los dieléctricos sea mayor que la unidad, se obtiene que la capacidad de un condensador relleno de dieléctrico en su interior es siempre mayor que la del mismo condensador en vacío.

En particular, para el caso de un condensador de placas planas y paralelas, relleno de un dieléctrico homogéneo de permitividad (absoluta) $\varepsilon$ , la capacidad se obtiene simplemente sustituyendo la permitividad del vacío por la del material

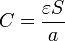
$C = \frac{\varepsilon S}{a}$

La energía de un sistema de conductores inmersos en dieléctricos lineales es también una extensión de la correspondiente para el vacío

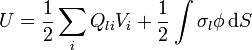
$U = \frac{1}{2}\sum_i Q_{li}V_i + \frac{1}{2}\int \sigma_l \phi\,\mathrm{d}S$

donde la última integral se refiere a la posible carga libre que puede haber en las superficies no conductoras (por ejemplo, porque dos dieléctricos se han cargado por frotamiento).