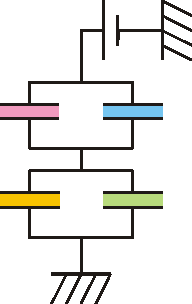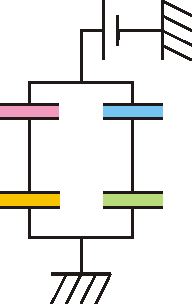Condensador con dos y con cuatro bloques de dieléctrico

De Laplace

Contenido

1 Enunciado
2 Caso de dos bloques
3 Caso de cuatro bloques

1 Enunciado

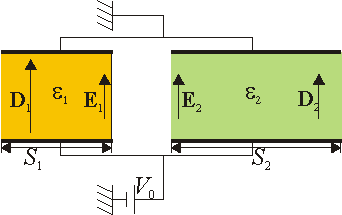
Repita el problema de dos dieléctricos entre dos placas suponiendo que la interfaz que separa los dieléctricos es perpendicular a las placas.

¿Se podría resolver un problema similar pero con cuatro dieléctricos, tal como muestra la figura? ¿Cuál sería el circuito equivalente?

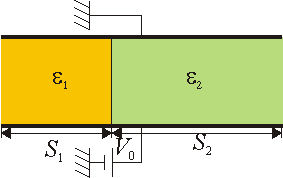
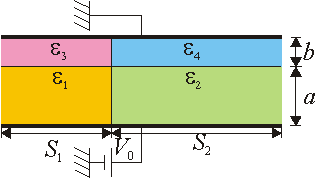
2 Caso de dos bloques

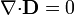Partiendo, como en el problema de las dos capas, de las ecuaciones $\nabla\times\mathbf{E}=\mathbf{0}$ y $\nabla{\cdot}\mathbf{D}=0$ , podemos establecer, al despreciar los efectos de borde, que el campo eléctrico en cada región es uniforme y va en la dirección perpendicular a las placas.

$\mathbf{E}=\begin{cases}E_1\mathbf{u}_{z} & x>0 \\ E_2\mathbf{u}_{z} & x<0\end{cases}$

De las dos condiciones de contorno aplicables en la frontera, la que no es trivial en este caso es la de las componentes tangenciales de $\mathbf{E}$

$\mathbf{n}\times[\mathbf{E}]=\mathbf{0}$ $\Rightarrow$

E 1 = E 2

ya que los campos sólo poseen componentes tangenciales en la interfaz.

Resulta así que el campo eléctrico posee el mismo valor en todo el espacio entre las placas.

Como, por otro lado, la diferencia de potencial entre placas es $V 0$ resulta

$\int_0^a\mathbf{E}_1{\cdot}\mathrm{d}\mathbf{r}=\int_0^a\mathbf{E}_2{\cdot}\mathrm{d}\mathbf{r}=V_0-V_a=V_0$

de donde

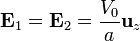
$\mathbf{E}_1=\mathbf{E}_2=\frac{V_0}{a}\mathbf{u}_{z}$

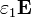Para hallar la carga almacenada en una de las placas, debemos obtener el flujo de $\mathbf{D}$ . El desplazamiento eléctrico vale $\varepsilon_1\mathbf{E}$ en una región y $\varepsilon_2\mathbf{E}$ en la otra (y es nulo en el exterior), de modo que

$Q=\oint\mathbf{D}{\cdot}\mathrm{d}\mathbf{S}=\frac{\varepsilon_1S_1V_0}{a}+\frac{\varepsilon_2S_2V_0}{a}$

(siendo $S 1$ y $S 2$ las áreas cubiertas por cada dieléctrico).

De aquí resulta la capacidad

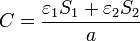
$C=\frac{\varepsilon_1S_1+\varepsilon_2S_2}{a}$

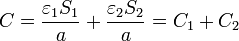
la cual se puede descomponer en $C=\frac{\varepsilon_1S_1}{a}+\frac{\varepsilon_2S_2}{a}=C_1+C_2$

que es la expresión de la capacidad de una asociación en paralelo de dos condensadores.

Esta expresión podía también haberse obtenido a partir de la energía almacenada en el sistema. Para ello, se considera la energía almacenada en el sistema y, a partir de la comparación con la expresión de la energía almacenada en una a asociación de condensadores, se deduce la capacidad equivalente del sistema

3 Caso de cuatro bloques

Si se intenta aplicar un cálculo similar al sistema de cuatro dieléctricos, tenemos cuatro superficies de separación y en ellas se conservan o bien las componentes tangenciales de $\mathbf{E}$ o las normales de $\mathbf{D}$ . Si despreciamos los efectos de borde y admitimos que los campos son uniformes en cada región, esto lleva a las identidades

Para las componentes tangenciales

$E_1=E_2\,$ $E_3=E_4\,$

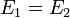
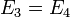
Para las componentes normales

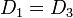
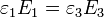
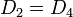
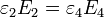
$D_1=D_3\,$ $\Rightarrow$ $\varepsilon_1E_1=\varepsilon_3E_3\,$ $D_2=D_4\,$ $\Rightarrow$ $\varepsilon_2E_2=\varepsilon_4E_4$

a las que hay que añadir la condición

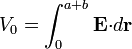
$V_0=\int_0^{a+b}\mathbf{E}{\cdot}d\mathbf{r}$

Esto nos da cinco ecuaciones para sólo cuatro incógnitas, por lo que este sistema no tendrá, en general, solución. Un sencillo cálculo establece que ésta existirá si

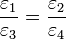
$\frac{\varepsilon_1}{\varepsilon_3}=\frac{\varepsilon_2}{\varepsilon_4}$

condición que no se verificará en general.

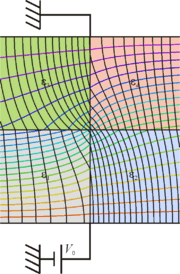
La respuesta no es, por supuesto, que este problema no tenga solución, sino que hemos hecho una simplificación excesiva al suponer que los campos son uniformes en cada región. En realidad los campos no son homogéneos. En la figura se muestra la solución numérica para las equipotenciales y las líneas de campo en el caso de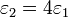 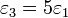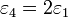$\varepsilon_2=4\varepsilon_1$ , $\varepsilon_3=5\varepsilon_1$ , $\varepsilon_4=2\varepsilon_1$ . En la miniatura se ve una ampliación de la zona central

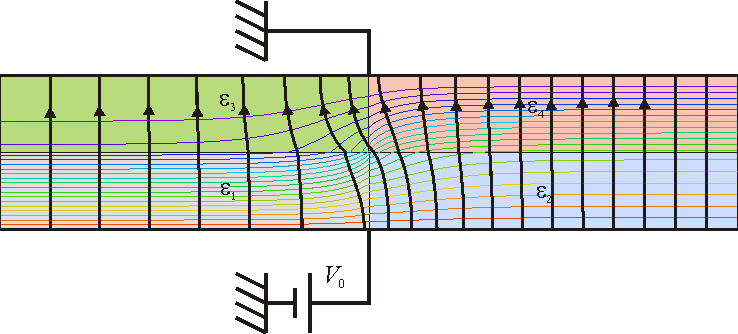
Una solución aproximada consiste en despreciar alguna de las condiciones. En este caso, la mejor solución posible consiste en olvidarse de la conservación de la componente tangencial de $\mathbf{E}$ y trabajar sólo con la normal de $\mathbf{D}$ . La razón es clara a partir de la figura anterior: salvo en una región en torno a la interfaz vertical central, en el resto del sistema el campo es prácticamente vertical.

En este caso, el sistema es análogo a una asociación en paralelo de dos condensadores, cada uno de los cuales es una asociación serie de dos como en el problema de dos capas.

Los dos circuitos que podrían ser equivalentes son los de las figura, aunque ninguno es correcto, siendo el más aproximado a la realidad el segundo.

Condensador con dos y con cuatro bloques de dieléctrico

De Laplace

Contenido

1 Enunciado

2 Caso de dos bloques

3 Caso de cuatro bloques

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES