Permitividad efectiva de la unión de dos materiales
De Laplace
Contenido |
1 Enunciado
Un condensador de placas planas y paralelas está relleno de dos capas del mismo espesor de materiales dieléctricos de permitividades relativas 3 y 5, siendo la interfaz paralela a las placas. ¿Cuánto vale la permitividad relativa promedio de este condensador?
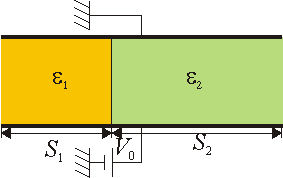
Suponga ahora que los dos materiales se encuentran en dos bloques adyacentes, ocupando cada uno la mitad de la sección. ¿Cuál es en ese caso la permitividad promedio?

2 Introducción
Este problema simplemente recoge los resultados del problema de dos capas que forman un sandwich y el de uno con dos bloques adyacentes. Aqui lo único que vamos a hacer es expresar el resultado en términos de una permitividad efectiva. Esto es, tanto en un caso como en otro, el condensador puede verse desde fuera como compuesto por un solo material, con una permitividad que será un promedio de las de los materiales que lo componen. Por tratarse de un promedio, este valor estará entre el mínimo y el máximo de las de los materiales, en este caso, estará entre 3 y 5.
En un caso general de una interfaz arbitraria, o el caso frecuente de un material con impurezas o porciones de otro material intercaladas, la permitividad promedio seguirá siendo un valor intermedio entre las dos extremos, pero su valor concreto requerirá en general el uso de métodos numéricos.
3 Capas en sandwich
Para el caso de dos capas en sandwich

o, lo que es lo mismo

El primer factor es la llamada media armónica de las dos permitividades relativas (la media armónica es tal que su inversa es la media aritmética de las inversas de los diferentes términos).

En este caso

El resultado se generaliza de manera inmediata a N capas de diferentes espesores

Si llamamos fi a la fracción del espesor total ocupado por cada capa

queda la media armónica ponderada

4 Bloques adyacentes
En el caso de dos bloques adyacentes resulta la media aritmética de las diferentes permitividades

con

En el caso de N bloques queda la media aritmética ponderada

siendo
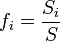
la fracción de sección ocupada por cada material.





