Entrar Página Discusión Historial Go to the site toolbox

Densidades de carga de polarización

De Laplace

Contenido

1 Introducción

2 Potencial debido a una polarización

3 Densidades de carga de polarización

La expresión del potencial debido a un volumen polarizado puede transformarse en suma de dos integrales

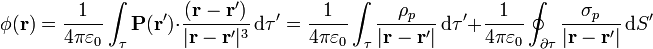
\phi(\mathbf{r}) =\frac{1}{4\pi\varepsilon_0}\int_\tau \mathbf{P}(\mathbf{r}'){\cdot}\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\,\mathrm{d}\tau' = \frac{1}{4\pi\varepsilon_0}\int_\tau\frac{\rho_p}{|\mathbf{r}-\mathbf{r}'|}\,\mathrm{d}\tau'+ \frac{1}{4\pi\varepsilon_0}\oint_{\partial\tau}\frac{\sigma_p}{|\mathbf{r}-\mathbf{r}'|}\,\mathrm{d}S'

donde

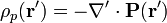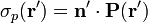
\rho_p(\mathbf{r}')=-\nabla'\cdot\mathbf{P}(\mathbf{r}')    y    \sigma_p(\mathbf{r}')=\mathbf{n}'\cdot\mathbf{P(\mathbf{r}')}

son las llamadas densidades de carga de polarización. Aquí 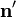\mathbf{n}' es la normal exterior a la superficie del material polarizado. Mantenemos la prima en el operador nabla y en el vector normal (aunque fuera de la integral no es imprescindible), para recordar que estamos hablando de una distribución de fuentes y que el volumen de integración es aquél en que hay polarización.

La ventaja de esta transformación en suma de dos integrales es que este tipo de integrales corresponden al potencial debido a distribuciones de carga eléctrica. De esta forma se reduce un problema nuevo (el potencial debido a una distribución continua de dipolos) a uno ya conocido (el potencial de distribuciones de cargas)

En términos físicos, esto equivale a decir que una polarización es equivalente a una superposición de dos distribuciones de carga, una volumétrica y otra superficial.

3.1 Volumétrica

La densidad volumétrica de carga de polarización tiene la expresión general

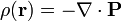
\rho(\mathbf{r})=-\nabla\cdot\mathbf{P}

Esta densidad de carga solo aparece en el interior de los dieléctricos, pues en el vacío 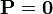\mathbf{P}=\mathbf{0} y su divergencia es nula.

Es posible dar una interpretación cualitativa de esta densidad volumétrica. Una polarización equivale a una cierta distribución de dipolos atómicos o moleculares. Para que haya una divergencia no nula, esta polarización no debe ser uniforme. Esto quiere decir que en a un lado de un punto del dieléctrico habrá más dipolos por unidad de volumen que en al otro lado. Si consideramos un entorno de este punto y que cada dipolo está formado por una carga positiva y una negativa iguales, lo que percibimos es que en dicho punto hay más de cargas de un signo que de otro y por tanto aparentemente una carga neta.

3.2 Superficial

Dado un bloque de material dieléctrico de volumen τ, la densidad superficial de carga de polarización en su frontera \partial\tau viene dada por la expresión

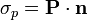
\sigma_p = \mathbf{P}\cdot\mathbf{n}

siendo \mathbf{n} la normal exterior al volumen.

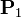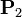Esta definición se puede generalizar al caso de que en lugar de una frontera exterior con el vacío tengamos una interfaz entre dos dieléctricos con polarizaciones \mathbf{P}_1 y \mathbf{P}_2. En ese caso, la densidad superficial de carga será la suma de las correspondientes a cada dieléctrico

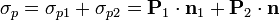
\sigma_p = \sigma_{p1}+\sigma_{p2}=\mathbf{P}_1\cdot\mathbf{n}_1+\mathbf{P}_2\cdot\mathbf{n}

Si, como es habitual a la hora de considerar condiciones de salto, llamamos \mathbf{n} a la normal a la interfaz que va del medio 1 al 2, tenemos que

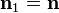
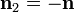
\mathbf{n}_1=\mathbf{n}    \mathbf{n}_2=-\mathbf{n}   \Rightarrow   \sigma_p = \mathbf{n}\cdot\left(\mathbf{P}_1-\mathbf{P}_2\right) = -\mathbf{n}\cdot[\mathbf{P}]

siendo

[\mathbf{P}]=\mathbf{P}_2-\mathbf{P}_1\,

el salto en la polarización al pasar de un medio al otro. Tenemos entonces la fórmula general

\sigma_p = -\mathbf{n}\cdot[\mathbf{P}]\,

que tiene una mayor analogía con la expresión correspondiente a la densidad volumétrica de carga.

3.3 Demostración

Para demostrar la equivalencia entre ambas expresiones, simplemente usamos la relación vectorial

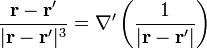
\frac{\mathbf{r}-\mathbf{r}'}{|\mathbf{r}-\mathbf{r}'|^3} = \nabla'\left(\frac{1}{|\mathbf{r}-\mathbf{r}'|}\right)

donde la prima sobre el operador nabla significa que las derivadas son respecto a las coordenadas con prima (las posiciones de las fuentes).

De esta forma el potencial debido a la polarización se puede escribir

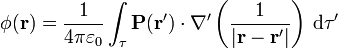
\phi(\mathbf{r}) = \frac{1}{4\pi\varepsilon_0}\int_\tau\mathbf{P}(\mathbf{r'})\cdot\nabla'\left(\frac{1}{|\mathbf{r}-\mathbf{r}'|}\right)\,\mathrm{d}\tau'

Usando ahora el álgebra del operador nabla

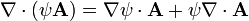
\nabla\cdot(\psi\mathbf{A}) = \nabla\psi\cdot\mathbf{A}+\psi\nabla\cdot\mathbf{A}

podemos transformar la integral en

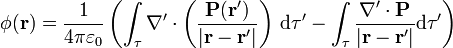
\phi(\mathbf{r}) = \frac{1}{4\pi\varepsilon_0}\left(\int_\tau\nabla'\cdot\left(\frac{\mathbf{P}(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}\right)\,\mathrm{d}\tau'-\int_\tau \frac{\nabla'\cdot\mathbf{P}}{|\mathbf{r}-\mathbf{r'}|}\mathrm{d}\tau'\right)

Aplicando el teorema de Gauss a la primera integral la transformamos en una de superficie

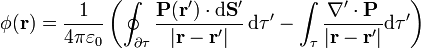
\phi(\mathbf{r}) = \frac{1}{4\pi\varepsilon_0}\left(\oint_{\partial\tau}\frac{\mathbf{P}(\mathbf{r}')\cdot\mathrm{d}\mathbf{S}'}{|\mathbf{r}-\mathbf{r}'|}\,\mathrm{d}\tau'-\int_\tau \frac{\nabla'\cdot\mathbf{P}}{|\mathbf{r}-\mathbf{r}'|}\mathrm{d}\tau'\right)

Aplicando que 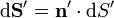\mathrm{d}\mathbf{S}'=\mathbf{n}'\cdot\mathrm{d}S' obtenemos finalmente la expresión deseada

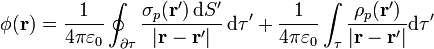
\phi(\mathbf{r}) = \frac{1}{4\pi\varepsilon_0}\oint_{\partial\tau}\frac{\sigma_p(\mathbf{r}')\,\mathrm{d}S'}{|\mathbf{r}-\mathbf{r}'|}\,\mathrm{d}\tau'+\frac{1}{4\pi\varepsilon_0}\int_\tau \frac{\rho_p(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}\mathrm{d}\tau'

4 Ventajas de usar σp y ρp

La introducción de las densidades de carga de polarización supone que transformamos una integral de volumen en dos nuevas integrales: una de volumen y una de superficie.

Aunque esto no parece un avance, la ventaja está en que las dos integrales son de un tipo conocido: potenciales debidos a densidades de carga eléctrica. Esto permite emplear una serie de métodos alternativos para el cálculo del potencial y del campo eléctrico, aparte de la integración directa. Así puede emplearse la ley de Gauss en situaciones de alta simetría (como en el caso de una esfera polarizada radialmente), o la solución de la ecuación de Poisson.

5 ¿Son reales las cargas de polarización?

Ésta es hasta cierto punto una pregunta metafísica, ya que en física no se dice si algo es real o no, sino si un modelo matemático se corresponde con al realidad o no. Y como todas las preguntas de este tipo, depende de qué entendamos por cargas reales.

Si consideramos cargas “reales” aquellas que corresponde a partículas cargadas (como electrones o protones) entonces no, las cargas de polarización no están asociadas a cargas individuales depositadas en partículas, sino a una cierta redistribución en un sistema neutro como un átomo.

Sin embargo, esa definición de carga es muy restrictiva, ya que en muchos casos ni siquiera cuando tenemos un cuerpo verdaderamente cargado (un conductor cargado, por ejemplo) podemos asociar esa carga con una partícula en concreto.

En su lugar, es siempre preferible dar una definición operacional, a partir de los efectos medibles que produce. Una carga eléctrica sería una fuente escalar que produce un campo eléctrico (medible a partir de las fuerzas que provoca). Con esta definición práctica, las densidades de carga de polarización son tan reales como cualquier otra, pues sí que producen campos eléctricos.

6 Densidad de carga libre

7 Carga y momento de ρp y σp

Como a toda densidad de carga, a la de polarización se le puede calcular sus momentos multipolares, con el fin de aproximar el potencial que produce una distribución de dipolos en puntos alejados de ella.

7.1 Carga neta

La carga neta (momento monopolar) de una distribución de carga de polarización es siempre nula

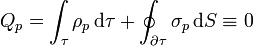
Q_p=\int_\tau \rho_p\,\mathrm{d}\tau+\oint_{\partial\tau}\sigma_p\,\mathrm{d}S\equiv 0

Este resultado es una consecuencia de que la distribución de carga de polarización es equivalente a un conjunto de dipolos. Puesto que cada dipolo es eléctricamente neutro, la carga total del sistema es nula.

Podemos demostrar este resultado a partir de las definiciones de ρp y σp, por aplicación del teorema de Gauss. Por un lado tenemos que

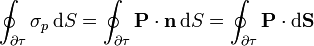
\oint_{\partial\tau}\sigma_p\,\mathrm{d}S=\oint_{\partial\tau}\mathbf{P}\cdot\mathbf{n}\,\mathrm{d}S=\oint_{\partial\tau}\mathbf{P}\cdot\mathrm{d}\mathbf{S}

y por otro

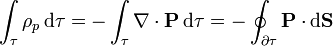
\int_{\tau}\rho_p\,\mathrm{d}\tau=-\int_{\tau}\nabla\cdot\mathbf{P}\,\mathrm{d}\tau=-\oint_{\partial\tau}\mathbf{P}\cdot\mathrm{d}\mathbf{S}

Sumando los dos términos

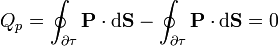
Q_p = \oint_{\partial\tau}\mathbf{P}\cdot\mathrm{d}\mathbf{S}-\oint_{\partial\tau}\mathbf{P}\cdot\mathrm{d}\mathbf{S} = 0

7.2 Momento dipolar

El momento dipolar de la distribución de cargas de polarización equivale a la integral de la polarización

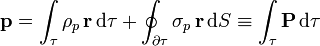
\mathbf{p}= \int_\tau \rho_p\,\mathbf{r}\,\mathrm{d}\tau+\oint_{\partial\tau}\sigma_p\,\mathbf{r}\,\mathrm{d}S \equiv\int_\tau\mathbf{P}\,\mathrm{d}\tau

De nuevo este resultado es elemental: si la polarización es la densidad de momento dipolar, su integral nos dará el momento dipolar total.

La demostración es similar a la anterior pero, al tratarse de vectores, es un poco más complicada. Puede hacerse considerando por separado cada una de las componentes cartesianas del momento dipolar.

8 Ecuaciones de la electrostática en dieléctricos

Obtenido de "http://tesla.us.es/wiki/index.php/Densidades_de_carga_de_polarizaci%C3%B3n"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 11:33, 22 feb 2010. - Esta página ha sido visitada 49.277 veces. - Aviso legal - Acerca de Laplace