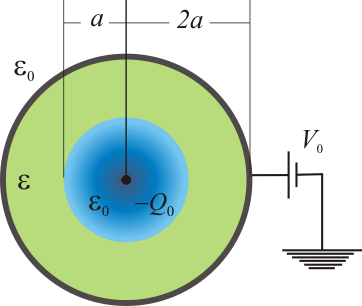
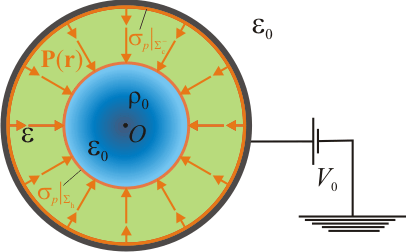
Esfera conductora rellena de dieléctrico con hueco
De Laplace
Contenido |
1 Enunciado
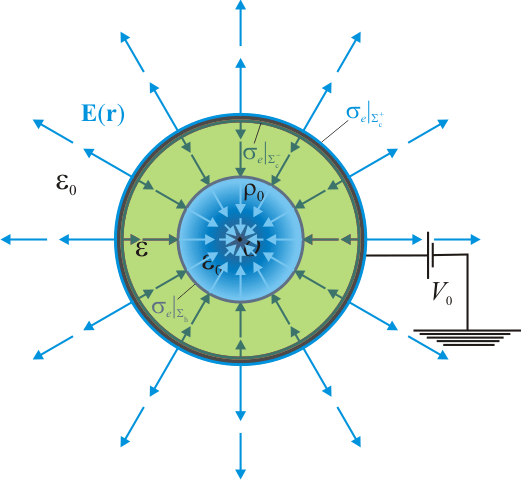
Una superficie esférica conductora ideal de pequeño espesor y radio 2a está rellena de un medio dieléctrico ideal homogéneo de permitividad , en cuyo centro hay un hueco de radio a. Estando la superficie conductora conectada a un potencial V0, el hueco es llenado con una nube de electrones cuya carga total es − Q0. Suponiendo que esta carga se distribuye uniformemente en el hueco y que en el medio dieléctrico no hay carga libre, resuelva las siguientes cuestiones:
, en cuyo centro hay un hueco de radio a. Estando la superficie conductora conectada a un potencial V0, el hueco es llenado con una nube de electrones cuya carga total es − Q0. Suponiendo que esta carga se distribuye uniformemente en el hueco y que en el medio dieléctrico no hay carga libre, resuelva las siguientes cuestiones:
- Determine los campos
 ,
,  y
y  , tanto en el interior como en el exterior de la esfera, antes y después de introducir la carga eléctrica en el hueco.
, tanto en el interior como en el exterior de la esfera, antes y después de introducir la carga eléctrica en el hueco.
- Halle la densidad de carga libre y la total en la interfaz r = a y en la cara interior y la exterior de la superficie conductora, antes y después de llenar el hueco.
- Calcule la energía electrostática almacenada en el sistema, antes y después de llenar el hueco.
2 Sin carga eléctrica en el hueco
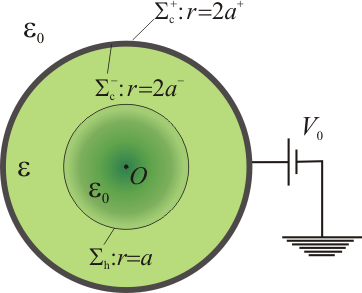
Analicemos primero el sistema antes de introducir los electrones en el hueco que hay en el centro del dieléctrico. Es decir, el sistema electrostático bajo estudio consiste en un conductor esférico de radio 2a y espesor despreciable, relleno de una cáscara esférica de material dieléctrico ideal de permitividad dieléctrica , y radios interior y exterior a y 2a, respectivamente. El conductor está conectado a una fuente de tensión constante de manera que la superficie conductora Σc va a ser una equipotencial de valor conocido V0.
, y radios interior y exterior a y 2a, respectivamente. El conductor está conectado a una fuente de tensión constante de manera que la superficie conductora Σc va a ser una equipotencial de valor conocido V0.
2.1 Campos eléctrico, de polarización y vector desplazamiento
La fuentes escalares de estos campos son las distribuciones de carga eléctrica. En el interior de la esfera sólo podría haber cargas de polarización, pues está ocupado por un dieléctrico ideal con un hueco vacío. En la superficie conductora a potencial V0 habrá cargas libres, pero también podría haber una densidad superficial de cargas de polarización en su cara interior  como consecuencia de una discontinuidad del campo de polarización en la interfaz dieléctrico-conductor. Si el valor del potencial es constante, estas distribuciones de carga no van a variar en el tiempo (sistema electrostático), de manera que el campo eléctrico creado por éstas será irrotacional y derivará del potencial electrostático
como consecuencia de una discontinuidad del campo de polarización en la interfaz dieléctrico-conductor. Si el valor del potencial es constante, estas distribuciones de carga no van a variar en el tiempo (sistema electrostático), de manera que el campo eléctrico creado por éstas será irrotacional y derivará del potencial electrostático 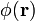 . Tomando el centro geométrico O como origen del sistema de referencia, dicho campo escalar deberá verificar las siguientes condiciones de contorno:
. Tomando el centro geométrico O como origen del sistema de referencia, dicho campo escalar deberá verificar las siguientes condiciones de contorno:

Teniendo en cuenta que las cargas eléctricas se distribuirán siguiendo la simetría esférica del sistema, podemos considerar que el valor del potencial en cualquier punto va a depender exclusivamente de su distancia al centro geométrico O. Como puede comprobarse, esta solución para el potencial es compatible con las condiciones de contorno antes indicadas. En consecuencia, el campo eléctrico será radial. Utilizando coordenadas esféricas, se tendrá,
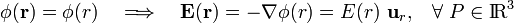
La región exterior al conductor esférico está vacía; es decir, no hay medios materiales ni tampoco carga eléctrica. Por tanto, el potencial electrostático en dicha región debe verificar la ecuación de Laplace, cuya solución en esféricas para un campo radial es bien conocida:
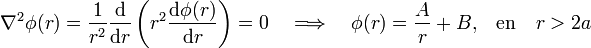
Las constantes A y B se determinan a partir de las condiciones de contorno, obteniéndose así la solución al problema del potencial y el campo eléctrico en los puntos exteriores a la esfera conductora:
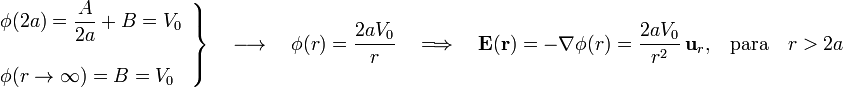
El campo de polarización 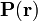 en la región exterior va a ser nulo por tratarse de espacio vacío. En consecuencia, el vector desplazamiento va a ser igual al campo eléctrico antes calculado, multiplicado por la permitividad dieléctrica del vacío
en la región exterior va a ser nulo por tratarse de espacio vacío. En consecuencia, el vector desplazamiento va a ser igual al campo eléctrico antes calculado, multiplicado por la permitividad dieléctrica del vacío  :
:
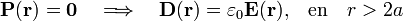
Como el interior de la esfera conductora está parcialmente relleno de un dieléctrico ideal no podemos plantear una ecuación para el potencial, pues desconocemos si hay cargas eléctricas de polarización y cómo se distribuyen éstas. Lo que sí podemos asegurar es que no puede haber cargas libres. Por tanto, en virtud de la ley de Gauss para el vector desplazamiento, podemos asegurar que el flujo de este campo a través de cualquier superficie cerrada incluida en la región r < 2a, es nulo.
Haciendo uso de que, tal como se discutió anterioremente, el campo eléctrico en cualquier punto del espacio debe ser radial, y que el interior de la esfera está ocupado por dieléctricos lineales (medio material y vacío) de simetría esférica, se llega a la conclusión de que el vector desplamiento en r < 2a también va a ser radial. Por tanto, si tomamos una superficie esférica  con centro en O y radio menor que 2a, se obtiene,
con centro en O y radio menor que 2a, se obtiene,

Es decir, el vector desplazamiento en cualquier punto interior a la superficie conductora es nulo, Y como dentro de ésta los medios son lineales, el campo eléctrico interior también va a ser nulo. En consecuencia, tampoco va a existir campo de polarización en el interior:

Resumiendo, el campo eléctrico, vector deplazamiento y polarización en la situación bajo estudio, son:
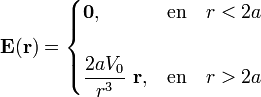
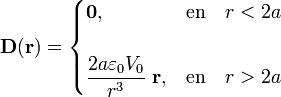

2.2 Densidades superficiales de carga eléctrica
Las distribuciones superficiales de cargas eléctricas están ligadas a la existencia de discontinuidades de los campos en superficies que separan medios de distinta naturaleza. En el sistema bajo estudio, esto ocurre en la interfaz hueco-dieléctrico, que hemos denomidado 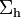 y en la cáscara conductora de espesor despreciable que hemos identificado como
y en la cáscara conductora de espesor despreciable que hemos identificado como 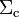 . Nótese que ésta constituye una doble interfaz: una dieléctrico-conductor en la cara interior,
. Nótese que ésta constituye una doble interfaz: una dieléctrico-conductor en la cara interior, 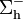 ; otra conductor-vacío en la cara exterior
; otra conductor-vacío en la cara exterior 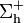
2.2.1 En la interfaz hueco-dieléctrico
Anteriormente obtuvimos que cuando el hueco está descargado, los campos en el interior de la esfera conductora son nulos, tanto en el hueco vacío (región r < a), como en el dieléctrio ideal que rellena la región a < r < 2a. Es decir, las componentes normales de los campos no sufren discontinuidad alguna en la superficie  y, por tanto, no habrá allí distribuciones superficiales de carga eléctrica:
y, por tanto, no habrá allí distribuciones superficiales de carga eléctrica:
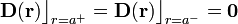

![\sigma_l\big\rfloor_{\Sigma_\mathrm{h}}=\mathbf{n}\cdot\bigg[\mathbf{D}\big\rfloor_{r=a^+}-\mathbf{D}\big\rfloor_{r=a^-}\bigg]=0](/wiki/images/math/f/7/2/f72defa8f423a0f898cd0e34d2e2ac93.png)


![\frac{\sigma_e}{\varepsilon_0}\bigg|_{\Sigma_\mathrm{h}}=\mathbf{n}\cdot\bigg[\mathbf{E}\big\rfloor_{r=a^+}-\mathbf{E}\big\rfloor_{r=a^-}\bigg]=0](/wiki/images/math/c/b/3/cb33c4f216246bdae1ed7f7592a8f465.png)
donde  es el vector normal a la superficie
es el vector normal a la superficie 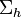 . Y si las distribuciones superficiales de carga libre
. Y si las distribuciones superficiales de carga libre 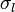 y de carga eléctrica total
y de carga eléctrica total 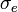 son nulas en esta interfaz, tampoco habrá cargas de polarización:
son nulas en esta interfaz, tampoco habrá cargas de polarización:
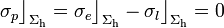
2.2.2 En la superficie conductora
Asumiendo que en la situación de equilibrio electrostático los campos  ,
,  y
y  son nulos en el interior conductor de la delgada corteza esférica (comportamiento de conductor ideal), las distribuciones de cargas eléctricas en dicha superficie conductora estarán determinadas por el valor de los campos en sus caras interior y exterior. Por tanto, en la cara interior
son nulos en el interior conductor de la delgada corteza esférica (comportamiento de conductor ideal), las distribuciones de cargas eléctricas en dicha superficie conductora estarán determinadas por el valor de los campos en sus caras interior y exterior. Por tanto, en la cara interior  no habrá ningún tipo de carga, ya que los campos son nulos dentro de la esfera de radio 2a:
no habrá ningún tipo de carga, ya que los campos son nulos dentro de la esfera de radio 2a:
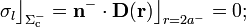


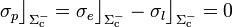
donde  es el vector unitario perpendicular a la superficie esférica de radio 2a y con el sentido hacia el interior; es decir,
es el vector unitario perpendicular a la superficie esférica de radio 2a y con el sentido hacia el interior; es decir, 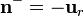 .
.
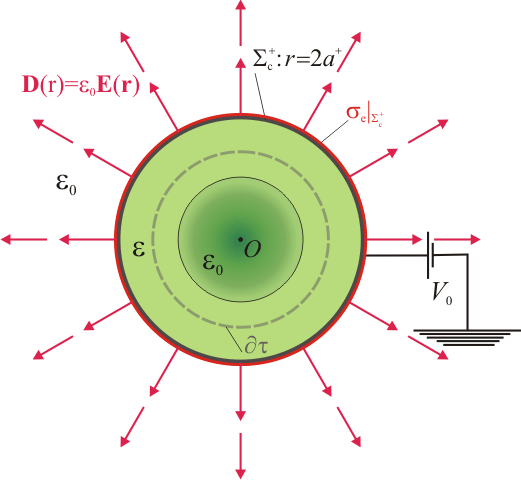
En la cara exterior 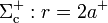 sí va a haber distribuciones superficiales de carga pues, según vimos en el apartado anterior, fuera de la esfera conductora si hay campos. Teniendo en cuenta que el vector normal a esta cara es
sí va a haber distribuciones superficiales de carga pues, según vimos en el apartado anterior, fuera de la esfera conductora si hay campos. Teniendo en cuenta que el vector normal a esta cara es 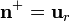 , se tendrá,
, se tendrá,
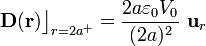

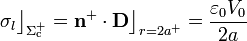
Es decir, en la cara exterior de la superficie conductora existe una distribución uniforme de carga eléctrica libre. La densidad superficial de carga eléctrica total está determinada por el valor del campo eléctrico en los puntos de dicha superficie. Como puede comprobarse, la distribución de carga total coincide con la de carga libre; es decir, el único tipo de carga eléctrica que hay en la cara exterior del conductor es carga libre:
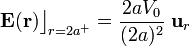




2.2.3 Distribuciones volumétricas
En el enunciado sólo se piden las distribuciones superficiales de carga pero, para completar el ejercicio calcularemos también las densidades volumétricas. La cuestión es simple: en la región interior a la superficie conductora no hay campo  ,
,  ni
ni  . Por tanto, las densidades volumétricas de carga eléctrica total, libre y de polarización (las respectivas divergencias de dichos campos), son nulas en todos los puntos tales que r < 2a. El exterior de la esfera es vacío y hemos resuelto el apartado 2.2 asumiendo que no hay ningún tipo de carga, por tanto, las densidades volumétricas en esta región deben ser nulas. Efectivamente, los campos eléctrico y vector desplazamiento calculados en dicho apartado son tales que sus diverfencias son nulas. El campo de polarización es nulo y, en consecuencia, la densidad volumétrica de carga de polarización va ser también nula en todos los puntos de la región r > 2a. En definitiva, obtenemos
. Por tanto, las densidades volumétricas de carga eléctrica total, libre y de polarización (las respectivas divergencias de dichos campos), son nulas en todos los puntos tales que r < 2a. El exterior de la esfera es vacío y hemos resuelto el apartado 2.2 asumiendo que no hay ningún tipo de carga, por tanto, las densidades volumétricas en esta región deben ser nulas. Efectivamente, los campos eléctrico y vector desplazamiento calculados en dicho apartado son tales que sus diverfencias son nulas. El campo de polarización es nulo y, en consecuencia, la densidad volumétrica de carga de polarización va ser también nula en todos los puntos de la región r > 2a. En definitiva, obtenemos
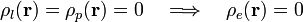
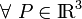
2.3 Energía electrostática
Aprovechando que hemos calculado cómo son el campo eléctrico y el vector desplazamiento en todo el espacio, podemos calcular la energía electrostática total almacenada  , integrando en
, integrando en 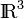 la función densidad de energía,
la función densidad de energía, 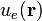 , que describe la cantidad de energía electrostática por unidad de volumen que hay en cada punto. Teniendo en cuenta que los campos
, que describe la cantidad de energía electrostática por unidad de volumen que hay en cada punto. Teniendo en cuenta que los campos 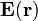 y
y 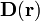 son nulos en la región interior de la esfera conductora, y que fuera de ella hay vacío, se tendrá que,
son nulos en la región interior de la esfera conductora, y que fuera de ella hay vacío, se tendrá que,
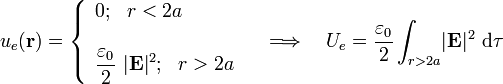
Teniendo en cuenta que los campos están expresados en coordenadas esféricas y utilizando la expresión del elemento de volumen en dichas coordenadas, se obtiene
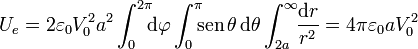
Puede comprobarse se obtiene este mismo resultado a partir de la distribución de carga libre en el sistema y del potencial: como sólo hay carga libre en la cara exterior de la superficie conductora, y ésta es una equipotencial de valor V0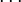
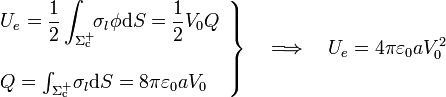
Por otra parte, puede comprobarse que la capacidad eléctrica de la esfera conductora es

3 Con carga eléctrica en el hueco
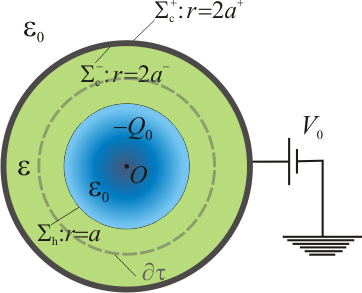
Consideremos ahora que el hueco esférico de radio a del centro del dieléctrico se rellena con una nube de electrones, mientras la corteza esférica conductora de radio 2a se mantiene conectada a la fuente de potencial V0. En virtud del teorema de Faraday, en la cara interior  de la corteza conductora se inducirá una cantidad de carga eléctrica igual a la que se halla en su interior, pero de signo opuesto. Y la carga eléctrica total que habrá en la región r < 2a es la carga libre negativa
de la corteza conductora se inducirá una cantidad de carga eléctrica igual a la que se halla en su interior, pero de signo opuesto. Y la carga eléctrica total que habrá en la región r < 2a es la carga libre negativa 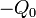 correspondiente a la nube eléctrónica del hueco más la carga de polarización inducida en el dieléctrico. Pero como todo el dieléctrico es interior a la corteza conductora, dicha carga de polarización total va a ser nula. En consecuencia, cabe esperar que en la superficie interior
correspondiente a la nube eléctrónica del hueco más la carga de polarización inducida en el dieléctrico. Pero como todo el dieléctrico es interior a la corteza conductora, dicha carga de polarización total va a ser nula. En consecuencia, cabe esperar que en la superficie interior  haya una cantidad
haya una cantidad  de carga libre. Además, podemos asegurar que esta carga se distribuirá uniformemente, ya que en el enunciado se indica que la nube electrónica es homogenea. Por tanto, tras llenar el hueco con electrones, el interior de la corteza esférica conductora sigue presentando una simetría esférica.
de carga libre. Además, podemos asegurar que esta carga se distribuirá uniformemente, ya que en el enunciado se indica que la nube electrónica es homogenea. Por tanto, tras llenar el hueco con electrones, el interior de la corteza esférica conductora sigue presentando una simetría esférica.
 sigue siendo la misma que calculamos en el apartado anterior, por lo que si continúa conectada a la fuente de potencial V0, soportará la misma cantidad
sigue siendo la misma que calculamos en el apartado anterior, por lo que si continúa conectada a la fuente de potencial V0, soportará la misma cantidad 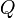 de carga libre que se obtuvo en el apartado 2.3. Por tanto, la cantidad total de carga eléctrica libre en la corteza conductora va a ser:
de carga libre que se obtuvo en el apartado 2.3. Por tanto, la cantidad total de carga eléctrica libre en la corteza conductora va a ser:
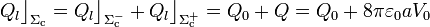
Por otra parte, como las condiciones exteriores tampoco han cambiado, la misma carga 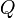 seguirá estando uniformemente distribuida en la cara exterior del conductor. Es decir, debido al apantallamiento producido por la delgada corteza conductora, la nube electrónica introducida en el hueco no modifica la densidad superficial de carga en
seguirá estando uniformemente distribuida en la cara exterior del conductor. Es decir, debido al apantallamiento producido por la delgada corteza conductora, la nube electrónica introducida en el hueco no modifica la densidad superficial de carga en  y, en consecuencia, aquélla no deberá tener efecto alguno sobre los campos en la región r > 2a. Comprobemos esto en el siguiente apartado.
y, en consecuencia, aquélla no deberá tener efecto alguno sobre los campos en la región r > 2a. Comprobemos esto en el siguiente apartado.
3.1 Campos eléctrico, de polarización y vector desplazamiento
Según acabamos de discutir, las distribuciones de carga en la nueva situación siguen presentado simetría esférica, por lo que generarán campos radiales. En particular, el potencial electrostático en todo el espacio será de la forma 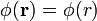 .
.
Como hemos dicho anteriormente, la región exterior r > 2a sigue estando exenta de carga eléctrica, por lo que el potencial verificará la ecuación de Laplace. Además las condiciones de contorno para el potencial en el infinito y en la superficie conductora también son las mismas que antes de introducir la nube electrónica. Por tanto, la solución al problema electrostático en r > 2a debe ser también la misma:

Efectivamente, como la corteza permanece conectada a la fuente de potencial V0, los campos en el exterior no sufren cambios respecto de los existentes antes de llenar el hueco de electrones. En la región interior sí se producirán cambios ya que la nube de electrones en el hueco dará lugar a la aparición de campos en r < 2a. Concretamente, existirá un campo eléctrico cuya fuentes serán tanto la carga libre
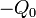 en r < a (hueco), como las cargas de polarización que se inducirán en el material dieléctrico que rellena la región a < r < 2a.
en r < a (hueco), como las cargas de polarización que se inducirán en el material dieléctrico que rellena la región a < r < 2a.
Pero no podemos calcular el campo  ya que no conocemos la distribución a priori de dichas cargas de polarización. Sin embargo, sabemos que la distribución conocida de carga libre en el hueco (nube de electrones) es la fuente escalar del vector desplazamiento
ya que no conocemos la distribución a priori de dichas cargas de polarización. Sin embargo, sabemos que la distribución conocida de carga libre en el hueco (nube de electrones) es la fuente escalar del vector desplazamiento 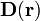 que hay en el interior de la esfera conductora. Para calcularlo, aplicamos de nuevo la ley de Gauss para el vector desplazamiento en una superficie cerrada
que hay en el interior de la esfera conductora. Para calcularlo, aplicamos de nuevo la ley de Gauss para el vector desplazamiento en una superficie cerrada  (gaussiana). Dada la simetría del sistema y teniendo en cuenta que los campos deben ser radiales, tomaremos una superficie esférica con centro en O y radio r < 2a, de manera que:
(gaussiana). Dada la simetría del sistema y teniendo en cuenta que los campos deben ser radiales, tomaremos una superficie esférica con centro en O y radio r < 2a, de manera que:
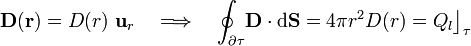
donde  es la cantidad de carga libre contenida en
es la cantidad de carga libre contenida en  . Obsérvese que esta cantidad de carga va a depender del radio de la superficie gaussiana. Teniendo en cuenta que en el dieléctrico no hay carga libre y que ésta se distribuye en el hueco uniformemente según una densidad volumetrica constante
. Obsérvese que esta cantidad de carga va a depender del radio de la superficie gaussiana. Teniendo en cuenta que en el dieléctrico no hay carga libre y que ésta se distribuye en el hueco uniformemente según una densidad volumetrica constante 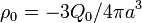 , se tendrá:
, se tendrá:
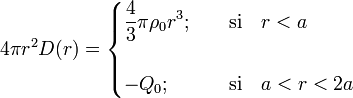

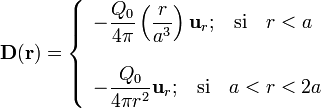
Por otra parte, en el hueco no hay moléculas que puedan polarizarse, por tanto no puede haber campo de polarización y el vector desplazamiento será igual al campo eléctrico multiplicado por la permitividad dieléctrica del vacío. En la región dieléctrica ideal sí habrá campo de polarización. Y al ser ésta lineal el vector desplazamiento es también proporcional al campo eléctrico, con  como constante de proporcionalidad:
como constante de proporcionalidad:


Haciendo uso de estas relaciones y de los resultados obtenidos anteriormente, se obtienen las siguientes expresiones para los campos vectoriales electrostáticos en todo el espacio cuando el hueco está relleno de una cantidad 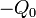 de carga libre y la superficie conductora se halla conectada a una fuente de potencial V0:
de carga libre y la superficie conductora se halla conectada a una fuente de potencial V0:
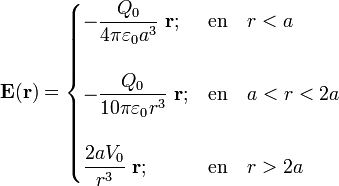
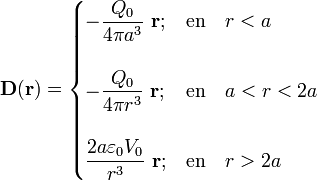
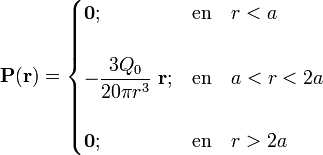
3.2 Densidades superficiales de carga eléctrica
Como ya hicimos anteriormente, estas densidades están directamente relacionadas con las discontinuidades de los campos que acabamos de calcular.
3.2.1 En la interfaz dieléctrico-hueco con carga
Las densidades superficiales de carga eléctrica total, carga libre y de polarización en la interfaz Σh:r = a son proporcionales a las discontinuidades que sufren los campos  ,
,  y
y  , respectivamente, en la dirección normal a dicha superficie, indicada por el vector unitario
, respectivamente, en la dirección normal a dicha superficie, indicada por el vector unitario 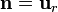 :
:
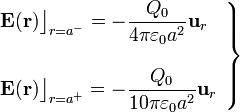

![\sigma_e\big\rfloor_{\Sigma_\mathrm{h}}=\varepsilon_0\ \mathbf{n}\cdot\bigg[\mathbf{E}\big\rfloor_{r=a^+}-\mathbf{E}\big\rfloor_{r=a^-}\bigg]=\frac{3Q_0}{20\pi a^2}](/wiki/images/math/c/c/4/cc4351e6630823dc870fc347fd3cfcc8.png)
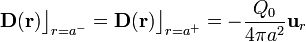

![\sigma_l\big\rfloor_{\Sigma_\mathrm{h}}=\mathbf{n}\cdot\bigg[\mathbf{D}\big\rfloor_{r=a^+}-\mathbf{D}\big\rfloor_{r=a^-}\bigg]=0](/wiki/images/math/f/7/2/f72defa8f423a0f898cd0e34d2e2ac93.png)
La continuidad de la componente normal del vector desplazamiento en esta interfaz indica que no hay cargas libres distribuidas en ella. En consecuencia, toda la carga eléctrica superficial es de polarización y, por tanto, debe ser también igual a la discontinuidad de la componente normal del vector de polarización:


![\sigma_p\big\rfloor_{\Sigma_\mathrm{h}}=-\mathbf{n}\cdot\bigg[\mathbf{P}\big\rfloor_{r=a^+}-\mathbf{P}\big\rfloor_{r=a^-}\bigg]=\frac{3Q_0}{20\pi a^2}=\sigma_e\big\rfloor_{\Sigma_\mathrm{h}}](/wiki/images/math/b/9/b/b9b7ddc1a6799cdae3eafc7ada7bd476.png)
3.2.2 En la superficie conductora
Como hemos visto, la carga 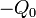 en el hueco no afecta a la distribución de carga eléctrica en la cara exterior del conductor, ni a los campos electrostáticos en la región r < 2a, y sólo van a depender del valor del potencial a que se encuentre dicho conductor. Como éste sigue siendo V0, las densidades de carga en
en el hueco no afecta a la distribución de carga eléctrica en la cara exterior del conductor, ni a los campos electrostáticos en la región r < 2a, y sólo van a depender del valor del potencial a que se encuentre dicho conductor. Como éste sigue siendo V0, las densidades de carga en 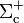 son las mismas que se obtuvieron para el caso del hueco vacío. La expresión de estas densidades puede obtenerse a partir del valor de la componente de los campos en r = 2a + , en la dirección y del vector normal
son las mismas que se obtuvieron para el caso del hueco vacío. La expresión de estas densidades puede obtenerse a partir del valor de la componente de los campos en r = 2a + , en la dirección y del vector normal 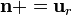 ; pero también pueden calcularse teniendo en cuenta que en dicha cara exterior sólo hay una cantidad
; pero también pueden calcularse teniendo en cuenta que en dicha cara exterior sólo hay una cantidad 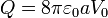 de carga cantidad de carga eléctrica libre que se distribuye uniformemente en la superficie esférica cuyo área es
de carga cantidad de carga eléctrica libre que se distribuye uniformemente en la superficie esférica cuyo área es  :
:

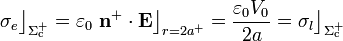



En la interfaz dieléctrico-conductor, correspondiente a la superficie 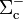 , sí se habrán producido cambios con respecto a la situación de "hueco vacío". Vimos que en aquel caso no había cargas eléctricas de ningún tipo en dicha interfaz. Ahora, tendremos tanto cargas libres distribuidas en la cara interior de la delgada corteza conductora, como cargas de polarización en la cara exterior del material dieléctrico ideal lineal que la rellena. Los valores de la componente normal de los campos en dicha interfaz determinan las correspondientes densidades superficiales de carga; tomando el vector unitario
, sí se habrán producido cambios con respecto a la situación de "hueco vacío". Vimos que en aquel caso no había cargas eléctricas de ningún tipo en dicha interfaz. Ahora, tendremos tanto cargas libres distribuidas en la cara interior de la delgada corteza conductora, como cargas de polarización en la cara exterior del material dieléctrico ideal lineal que la rellena. Los valores de la componente normal de los campos en dicha interfaz determinan las correspondientes densidades superficiales de carga; tomando el vector unitario 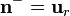 normal a la cara interior del conductor, se tendrá:
normal a la cara interior del conductor, se tendrá:


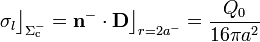
Obsérvese que esta densidad superficial describe cómo se distribuye la carga libre positiva  inducida en la cara interior del conductor, debido a la presencia de la carga
inducida en la cara interior del conductor, debido a la presencia de la carga 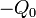 en el hueco. Además, el campo de polarización
en el hueco. Además, el campo de polarización  en el material dieléctrico implica la existencia de cargas de polarización en la superficie de contacto del dieléctrico con la cara interior del conductor:
en el material dieléctrico implica la existencia de cargas de polarización en la superficie de contacto del dieléctrico con la cara interior del conductor:
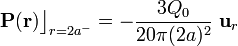

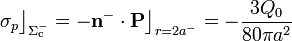
La densidad de carga eléctrica total en la superficie 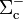 es igual al valor de la componente normal del campo eléctrico en dicha superficie, multiplicada por la permitividad dieléctrica del vacío. Y como dicha superficie es la interfaz dieléctrico-conductor, también va a ser igual a la suma de las densidades de carga libre y de polarización que acabamos de calcular:
es igual al valor de la componente normal del campo eléctrico en dicha superficie, multiplicada por la permitividad dieléctrica del vacío. Y como dicha superficie es la interfaz dieléctrico-conductor, también va a ser igual a la suma de las densidades de carga libre y de polarización que acabamos de calcular:
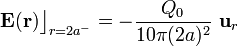


3.3 Distribuciones volumetricas
Una vez que hemos determinado los campos vectoriales en todo el espacio podemos obtener la distrubuciones volumétricas de sus fuentes escalares (densidades volumetricas de carga) calculando las divergencias de aquéllos:
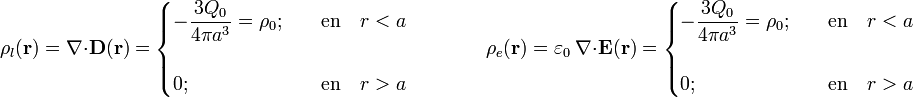
Es decir, la única distribución volumétrica de carga eléctrica es la carga libre negativa (nube de electrones) que rellena el hueco.

3.4 Energía electrostática
Seguiremos el mismo procedimiento que en el caso del hueco vacío, pero ahora tenemos que dentro de la esfera hay campos y, por tanto, energía electrostática almacenada. Como el dieléctrico que rellena parcialmente la esfera es lineal, la densidad de energía en cada punto de dicho medio es también igual a la mitad del producto escalar del campo eléctrico por el vector desplazamiento:
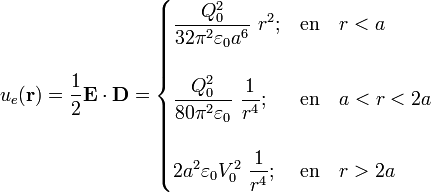
Es decir, la energía se almacena en las tres regiones diferenciadas del sistema. Sin embargo, como los campos fuera de la esfera no han cambiado, tampoco lo habrá hecho la cantidad de energía allí distribuida:
 con
con 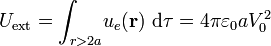
Calculamos las cantidades parciales parciales de energía que se localizan en el hueco relleno de carga libre negativa, 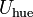 , y en el material dieléctrico,
, y en el material dieléctrico,  :
:
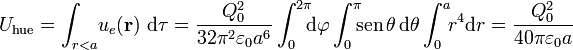

Finlmente se obtiene que la energía eléctrostática total almacenada en el sistema tras introducir la nube de electrones en el hueco del dieléctrico es: