Esfera polarizada uniformemente

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

Se tiene una esfera dieléctrica de radio

R

polarizada uniformemente con $\mathbf{P}=\mathbf{P}_0$ .

Halle, por integración directa el potencial eléctrico en todos los puntos del espacio.
¿Cuáles son los valores de $\mathbf{E}$ , $\mathbf{D}$ y $\mathbf{P}$ dentro y fuera de la esfera?
¿Cuánto valen las densidades de carga equivalentes a la polarización?

2 Solución

2.1 Potencial eléctrico

Para hallar el potencial por integración directa debemos emplear el hecho de que el potencial creado por un dipolo puntual es

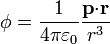
$\phi=\frac{1}{4\pi\varepsilon_0}\frac{\mathbf{p}{\cdot}\mathbf{r}}{r^3}$

donde $\mathbf{r}$ es el vector que va desde el punto donde se encuentra el dipolo al punto en que se mide el potencial.

Si tenemos una distribución de dipolos, descrita por la polarización \mathbf{P} el potencial total será la integral

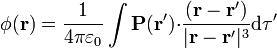
$\phi(\mathbf{r})=\frac{1}{4\pi\varepsilon_0}\int\mathbf{P}(\mathbf{r}'){\cdot}\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\mathrm{d}\tau'$

donde la integral se calcula sobre todos los puntos donde la polarización no es nula. Esta expresión es análoga a la que se da para una distribución de carga a partir del potencial de una carga puntual.

En nuestro caso $\mathbf{P}=\mathbf{P}_0$ dentro de la esfera y cero fuera, por lo que podemos sacar la polarización fuera de la integral y escribir el potencial como

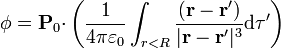
$\phi=\mathbf{P}_0{\cdot}\left(\frac{1}{4\pi\varepsilon_0} \int_{r<R}\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\mathrm{d}\tau'\right)$

donde la integral se calcula en la esfera de centro el origen y radio $R$ .

La integral que debemos calcular es bastante complicada. Así, por ejemplo, la componente $z$ podemos expresarla en esféricas y escribirla como

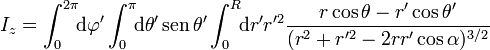
$I_z=\int_0^{2\pi}\!\! \mathrm{d}\varphi'\int_0^\pi\!\! \mathrm{d}\theta'\,\mathrm{sen}\,\theta'\int_0^R\!\! \mathrm{d}r' r'^2 \frac{r\cos\theta-r'\cos\theta'}{(r^2+r'^2-2rr'\cos\alpha)^{3/2}}$

con

$\cos\alpha=\,\mathrm{sen}\,\theta\,\mathrm{sen}\,\theta'\cos(\varphi-\varphi')+\cos\theta\cos\theta'$

No obstante, podemos ahorrarnos todo el cálculo si en este punto recordamos que el campo creado por una cierta distribución de carga es

$\mathbf{E}(\mathbf{r})=\frac{1}{4\pi\varepsilon_0} \int\frac{\rho(\mathbf{r}')(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\mathrm{d}\tau'$

y, en particular si tenemos una distribución de carga uniforme unitaria en una esfera de radio $R$ ( $ρ = 1$ dentro y cero fuera) el campo es

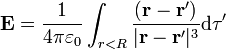
$\mathbf{E}=\frac{1}{4\pi\varepsilon_0} \int_{r<R}\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\mathrm{d}\tau'$

Ésta es precisamente la integral que aparece multiplicando a 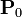$\mathbf{P}_0$ en la expresión del potencial. Por tanto, a partir del conocimiento de dicho campo podemos calcular el potencial en nuestro problema. Pero el valor del campo creado por una esfera de carga es conocido. Su valor es

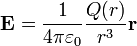
$\mathbf{E}=\frac{1}{4\pi\varepsilon_0} \frac{Q(r)}{r^3}\mathbf{r}$

con $Q (r)$ la carga encerrada dentro de una esfera de radio $r$ . En nuestro caso esto da

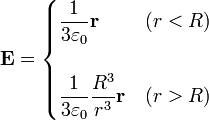
$\mathbf{E}=\begin{cases} \displaystyle\frac{1}{3\varepsilon_0}\mathbf{r} & (r<R)\\ & \\ \displaystyle\frac{1}{3\varepsilon_0}\displaystyle\frac{R^3}{r^3}\mathbf{r} & (r>R)\end{cases}$

por lo que el potencial de nuestro problema es

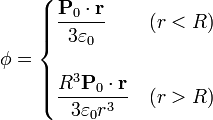
$\phi=\begin{cases}\displaystyle\frac{\mathbf{P}_0\cdot\mathbf{r}}{3\varepsilon_0} & (r<R)\\ & \\ \displaystyle\frac{R^3\mathbf{P}_0\cdot\mathbf{r}}{3\varepsilon_0r^3} & (r>R)\end{cases}$

y ya está resuelto el problema.

Obsérvese que en ningún momento se dice que el campo debido a una distribución de dipolos sea el de una esfera de carga uniforme. Lo único que se hace es emplear este último campo como herramienta de cálculo para hallar el potencial de la distribución de dipolos.

2.2 Campo y desplazamiento

2.2.1 En el interior de la esfera

En el interior de la esfera, vemos que el potencial corresponde a un campo constante de valor

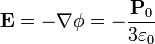
$\mathbf{E}=-\nabla\phi=-\frac{\mathbf{P}_0}{3\varepsilon_0}$

que va en sentido opuesto a la polarización.

El desplazamiento eléctrico en el interior de la esfera es también uniforme

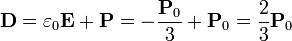
$\mathbf{D}=\varepsilon_0\mathbf{E}+\mathbf{P}=-\frac{\mathbf{P}_0}{3}+\mathbf{P}_0=\frac{2}{3}\mathbf{P}_0$

2.2.2 En el exterior de la esfera

El potencial exterior, en cambio, tiene la forma del potencial creado por un dipolo puntual

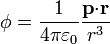
$\phi=\frac{1}{4\pi\varepsilon_0} \frac{\mathbf{p}{\cdot}\mathbf{r}}{r^3}$

si identificamos

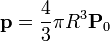
$\mathbf{p}=\frac{4}{3}\pi R^3\mathbf{P}_0$

así pues, desde fuera el potencial es el mismo que crearía un dipolo puntual situado en el origen y con momento dipolar igual al momento dipolar total de la esfera. Por ello, esta distribución puede servir para modelar dipolos reales, que no son estrictamente puntuales.

El campo eléctrico en el exterior será el debido a un dipolo puntual

$\mathbf{E}=\frac{1}{4\pi\varepsilon_0}\,\frac{3(\mathbf{p}{\cdot}\mathbf{r})\mathbf{r}-r^2\mathbf{p}}{r^5}$

y el desplazamiento será proporcional a él, pues la polarización es nula en el exterior de la esfera.

$\mathbf{D}=\varepsilon_0 \mathbf{E}+\mathbf{P}=\varepsilon_0\mathbf{E}$

Nótese que, en el exterior de la esfera, el desplazamiento eléctrico va en la misma dirección y sentido que el campo eléctrico, mientras que en el interior va en el sentido opuesto.

2.3 Cargas de polarización

2.3.1 De volumen

La densidad volumétrica de carga de polarización es

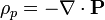
$\rho_p = -\nabla\cdot\mathbf{P}$

y esta cantidad es nula tanto dentro como fuera de la esfera. Fuera porque la polarización es nula y dentro porque es uniforme. Por tanto

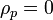
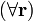
$\rho_p = 0\,$ $(\forall\mathbf{r})\,$

2.3.2 De superficie

Las posibles densidades superficiales de carga de polarización se encontrarán en las interfaces entre ergiones. En este caso la única que hay es la propia superficie de la esfera. En ella

$\sigma_p=-\mathbf{n}\cdot[\mathbf{P}] = -\mathbf{u}_r\cdot\left(\mathbf{0}-\mathbf{P}_0\right) = \mathbf{u}_r\cdot\mathbf{P}_0$

Si tomamos el eje z como el definido por la polarización

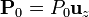
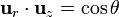
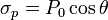
$\mathbf{P}_0 = P_0\mathbf{u}_z$ $\mathbf{u}_r\cdot\mathbf{u}_z = \cos\theta\,$ $\,\sigma_p = P_0\cos\theta$

Esta densidad de carga es positiva en el hemisferio “norte” definido como aquél al que apunta la polarización, y negativa en el “sur”. En el “ecuador” de la esfera la densidad de carga es nula.

2.4 Expresión en coordenadas esféricas

Puede ser interesante, para otras referencias, expresar los resultados anteriores en coordenadas esféricas.

Tomando como eje z el marcado por la polarización, ésta se escribe

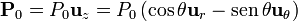
$\mathbf{P}_0=P_0\mathbf{u}_z = P_0\left(\cos\theta\mathbf{u}_r-\mathrm{sen}\,\theta\mathbf{u}_\theta\right)$

2.4.1 Potencial

Una vez que tenemos la polarización, sustituimos en la expresión del potencial. El resultado es, en el interior de la esfera

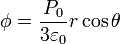$\phi = \frac{P_0}{3\varepsilon_0}r\cos\theta$

(r < R)

y en el exterior

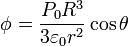$\phi = \frac{P_0R^3}{3\varepsilon_0r^2}\cos\theta$

(r > R)

Podemos ver que se trata de una función continua, ya que

$[\phi] = \phi(R^+)-\phi(R^-) = \left(\frac{P_0R^3}{3\varepsilon_0R^2}-\frac{P_0R}{3\varepsilon_0}\right)\cos\theta =0$

2.4.2 Campo eléctrico

A partir de la expresión del potencial hallamos el campo eléctrico a partir del gradiente:

$\mathbf{E}=-\nabla\phi = \begin{cases}\displaystyle\frac{P_0}{3\varepsilon_0}\left(-\cos\theta\mathbf{u}_r+\mathrm{sen}\,\theta\mathbf{u}_\theta\right) & (r<R) \\ & \\ \displaystyle\frac{P_0R^3}{3\varepsilon_0r^3}\left(2\cos\theta\mathbf{u}_r+\mathrm{sen}\,\theta\mathbf{u}_\theta\right) & (r>R) \end{cases}$

A ambos lados de la interfaz este campo vale

$\begin{array}{rcl} \mathbf{E}(R^-) & = & \displaystyle \frac{P_0}{3\varepsilon_0}\left(-\cos\theta\mathbf{u}_r+\mathrm{sen}\,\theta\mathbf{u}_\theta\right)\\ & & \\ \mathbf{E}(R^+) & = & \displaystyle \frac{P_0}{3\varepsilon_0}\left(2\cos\theta\mathbf{u}_r+\mathrm{sen}\,\theta\mathbf{u}_\theta\right)\end{array}$

Podemos ver que se verifica la continuidad en la interfaz de la componente tangencial del campo eléctrico (marcada por 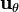$\mathbf{u}_\theta$ ), mientras que la componente normal (marcada por 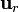$\mathbf{u}_r$ )es discontinua, estando su salto dado por la densidad superficial de carga (de polarización).

2.4.3 Desplazamiento

Conocida la polarización y el campo hallamos el desplazamiento eléctrico

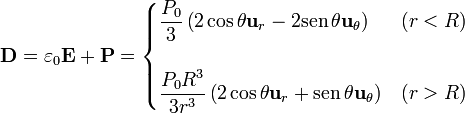
$\mathbf{D}=\varepsilon_0\mathbf{E}+\mathbf{P} = \begin{cases}\displaystyle\frac{P_0}{3}\left(2\cos\theta\mathbf{u}_r-2\mathrm{sen}\,\theta\mathbf{u}_\theta\right) & (r<R) \\ & \\ \displaystyle\frac{P_0R^3}{3r^3}\left(2\cos\theta\mathbf{u}_r+\mathrm{sen}\,\theta\mathbf{u}_\theta\right) & (r>R) \end{cases}$

que a ambos lados de la interfaz vale

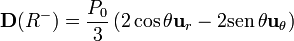
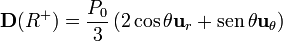
$\mathbf{D}(R^-) = \frac{P_0}{3}\left(2\cos\theta\mathbf{u}_r-2\mathrm{sen}\,\theta\mathbf{u}_\theta\right)$ $\mathbf{D}(R^+) = \frac{P_0}{3}\left(2\cos\theta\mathbf{u}_r+\mathrm{sen}\,\theta\mathbf{u}_\theta\right)$

A diferencia del campo eléctrico, el vector desplamiento es continuo en su componente normal (como corresponde a que no hay carga libre en la superficie), pero discontínuo en la componente tangencial (ya que el vector desplazamiento sí posee fuentes vectoriales).

Esfera polarizada uniformemente

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Potencial eléctrico

2.2 Campo y desplazamiento

2.2.1 En el interior de la esfera

2.2.2 En el exterior de la esfera

2.3 Cargas de polarización

2.3.1 De volumen

2.3.2 De superficie

2.4 Expresión en coordenadas esféricas

2.4.1 Potencial

2.4.2 Campo eléctrico

2.4.3 Desplazamiento

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES