Corriente eléctrica
De Laplace
1 Introducción
2 Densidades de corriente e intensidad de corriente
2.1 Densidad volumétrica de corriente
En situaciones no estáticas, las cargas que forman un sistema se encuentran en movimiento. Aunque todas las cargas que forman un material se encuentran en constante agitación, sólo una parte de ellas (los llamados portadores de carga poseen una velocidad promedio distinta de cero. La magnitud macroscópica que describe este movimiento colectivo es la densidad de corriente, definida como
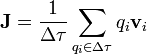
siendo su unidad en el SI 1 A/m².
Esta densidad de corriente no tiene una relación directa con la densidad de carga, ya que es perfectamente posible que en un punto de un conductor la densidad de carga se anule (porque haya tantas cargas positivas como negativas), mientras que la densidad de corriente sea distinta de cero (por ejemplo, porque las negativas se estén moviendo y las positivas no). Sí existe relación con la densidad de portadores. Dentro de un material en el cual existe movimiento de cargas por el desplazamiento de una o varias especies (tipos de portadores, por ejemplo, en agua salada tendríamos al menos cuatro especies: OH−, H3O+, Cl−, Na+), la densidad de corriente puede escribirse como
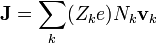
siendo Nk la densidad de cada especie, 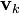 su velocidad neta promedio, o velocidad de arrastre, normalmente muy pequeña, y Zke su carga. En el caso común de un metal, en el que sólo los electrones se mueven
su velocidad neta promedio, o velocidad de arrastre, normalmente muy pequeña, y Zke su carga. En el caso común de un metal, en el que sólo los electrones se mueven 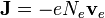 . En un semiconductor tendremos un término debido a los electrones y otro debido a los huecos.
. En un semiconductor tendremos un término debido a los electrones y otro debido a los huecos.
2.2 Densidad superficial de corriente
Del mismo modo que se define la densidad de corriente volumétrica también puede definirse la densidad de corriente superficial
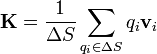
Esta densidad será de interés cuando tengamos que los portadores de carga están concentrados en las superficies de los materiales.
2.3 Intensidad de corriente
Si consideramos el flujo de carga que atraviesa una determinada sección S de un conductor, el resultado es la intensidad de corriente
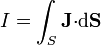
Físicamente, la intensidad de corriente proporciona la cantidad de carga que atraviesa la sección S en un intervalo de tiempo pequeño
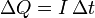
La intensidad de corriente, que se mide en amperios (A) en el SI, es un escalar con signo, indicando si el flujo es el sentido de la normal a la superficie o en el opuesto.
En el caso de una densidad de corriente superficial, puede obtenerse la intensidad de corriente que atraviesa una curva Γ (trazada sobre la superficie, y que es atravesada por la corriente) como
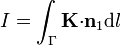
siendo 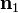 un vector tangente a la superficie y normal a la curva Γ.
un vector tangente a la superficie y normal a la curva Γ.
3 Ley de conservación de la carga
Una de las propiedades básicas de la interacción electromagnética es que la carga se conserva localmente, esto es, no puede crearse ni destruirse una carga neta en ningún punto. Esto se traduce matemáticamente en que si en un volumen τ la carga contenida disminuye, ello se debe al flujo al exterior a través de la frontera:
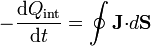
La versión diferencial de esta ley se escribe

Asociada a la ley de conservación de la carga existe una condición de salto que relaciona las densidades de corriente a ambos lados de una interfaz entre dos medios. Esta condición es, en general
![\mathbf{n}{\cdot}[\mathbf{J}] + \nabla_s{\cdot}\mathbf{K} + \frac{\partial\sigma_s}{\partial t}=0](/wiki/images/math/c/6/f/c6f6ea41accc6beef240415c3e40be5a.png)
siendo 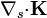 la divergencia superficial de la densidad de corriente superficial. En muchos casos prácticos, no obstante, este término está ausente y la condición se reduce a una que liga el salto en
la divergencia superficial de la densidad de corriente superficial. En muchos casos prácticos, no obstante, este término está ausente y la condición se reduce a una que liga el salto en 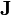 con la variación de cargas en la superficie.
con la variación de cargas en la superficie.
En situaciones de corrientes estacionarias (independientes del tiempo), la densidad de corriente resulta ser un campo solenoidal
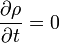

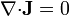
Esto implica que, para corrientes estacionarias, si consideramos un tubo de corriente, la intensidad en dos secciones cualesquiera de él es la misma
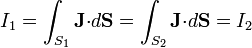
En situaciones no estacionarias esto no será cierto en general, ya que podrá haber acumulación de carga en los puntos intermedios.
En situaciones estacionarias la condición de salto (siempre que 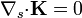 ) se reduce a
) se reduce a
![\mathbf{n}{\cdot}[\mathbf{J}]=0](/wiki/images/math/a/d/6/ad621ced2218bcb1b784a17006bc2129.png)
esto es, que la corriente que llega normalmente a la superficie debe coincidir con la que sale de ella.
En el caso particular de un electrodo perfectamente conductor, sumergido en un material por el cual puede fluir una corriente 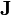 , pero además alimentado por un cable (que lo une a un generador, por ejemplo), la ley de conservación de la carga puede desglosarse, separando la corriente que fluye por el medio, de la que entra hacia el electrodo por el cable de alimentación. Si denominamos I a esta última, la ley de conservación en forma integral queda
, pero además alimentado por un cable (que lo une a un generador, por ejemplo), la ley de conservación de la carga puede desglosarse, separando la corriente que fluye por el medio, de la que entra hacia el electrodo por el cable de alimentación. Si denominamos I a esta última, la ley de conservación en forma integral queda
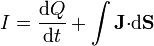
donde Q es la carga almacenada en el electrodo y el flujo de 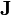 se calcula a través del material que rodea al electrodo, excluyendo el cable. En esta forma, la ecuación se interpreta como que la corriente que llega al electrodo, parte se emplea en aumentar la carga almacenada y parte se escapa a través del medio circundante (lo que se denominan pérdidas). Nótese que sólo para esta clase de sistemas, y exclusivamente en el caso de que no haya pérdidas, se verificará la relación I = dQ / dt, que en ningún caso puede considerarse una definición de intensidad de corriente, sino sólo como un caso muy particular de la ley de conservación de la carga.
se calcula a través del material que rodea al electrodo, excluyendo el cable. En esta forma, la ecuación se interpreta como que la corriente que llega al electrodo, parte se emplea en aumentar la carga almacenada y parte se escapa a través del medio circundante (lo que se denominan pérdidas). Nótese que sólo para esta clase de sistemas, y exclusivamente en el caso de que no haya pérdidas, se verificará la relación I = dQ / dt, que en ningún caso puede considerarse una definición de intensidad de corriente, sino sólo como un caso muy particular de la ley de conservación de la carga.
4 Ecuaciones del campo y de la corriente
4.1 En el estado estacionario
Para obtener las distribuciones de corrientes de campos y corrientes en situaciones estacionarias, tenemos las ecuaciones
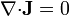

4.2 En situaciones dependientes del tiempo
5 Conductividad. Ley de Ohm
Como ocurre con los dieléctricos ideales, las ecuaciones de la divergencia de un campo y el rotacional de otro no son suficientes, ya que debemos tener una relación constitutiva que ligue la densidad de corriente con el campo que la produce.
En principio, dicha relación depende de la naturaleza del material conductor ya que no es lo mismo una disolución salina, que un metal,
que un semiconductor o que un plasma. Sin embargo, se encuentra que para una gran variedad de situaciones, la relación entre 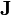 y
y  es de simple proporcionalidad
es de simple proporcionalidad
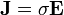
siendo ésta la llamada ley de Ohm. La constante de proporcionalidad σ es la conductividad, que se mide en Siemens/metro (S/m) en el SI y que describe la facilidad con que las cargas fluyen a través del material. Los valores de σ abarcan un amplísimo rango, desde casi 108 S/m para muy buenos conductores como la plata y el cobre hasta valores tan bajos como 10−14 S/m para dieléctricos muy aislantes.
En ocasiones, en lugar de la conductividad se emplea como parámetro su inversa, la resistividad, r = 1 / σ, que se mide en Ohmios·metro (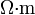 ).
).
En los materiales óhmicos, la determinación del potencial eléctrico es muy parecida al cálculo en materiales dieléctricos lineales, empleando la conductividad en lugar de la permitividad. Se trata de resolver
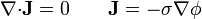
con las condiciones de salto
![\mathbf{n}\times[\mathbf{E}]=\mathbf{0}](/wiki/images/math/6/d/9/6d9a6f945a9f8273282ed8720257a0ba.png)
![\mathbf{n}{\cdot}[\mathbf{J}]=0](/wiki/images/math/a/d/6/ad621ced2218bcb1b784a17006bc2129.png)
a las que hay que añadir las condiciones de contorno en aquellas superficies cuya tensión esté fijada, y las correspondientes a las superficies libres (en cuyo exterior está el vacío o un dieléctrico ideal) para las cuales Jn = 0.
6 Conductores filiformes
De entre los distintos conductores óhmicos, una configuración muy común es la del conductor filiforme, en el cual las dimensiones laterales del conductor son mucho más pequeñas que su radio de curvatura. El ejemplo más común es un cable conector.
Cuando se aplica una diferencia de potencial VA − VB entre los extremos de un cable, se establece una corriente I a lo largo de él, cuya densidad se puede suponer paralela al cable y uniforme sobre una sección transversal. En este caso, se verifica
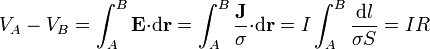
La cantidad R es la resistencia del conductor filiforme, medida en Ω en el SI. A esta relación entre voltaje y corriente también se la suele denominar ley de Ohm.
En el caso particular de un cable de longitud y conductividad constantes, la resistencia se reduce a R = l / (σS).
La inversa de la resistencia se denomina conductancia, G y su unidad en el SI es el Siemens (1 S=1 Ω-1). Para un conductor filiforme
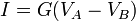
7 Coeficientes de conductancia y circuitos equivalentes
7.1 Coeficientes de conductancia
Un problema común de corrientes estacionarias en materiales óhmicos es la determinación de las corrientes que fluyen entre electrodos conductores perfectos, sumergidos en materiales resistivos. Este problema general incluye desde el caso común de un circuito con terminales conectados por cables, hasta situaciones generales de corrientes distribuidas en un fluido conductor como el agua.
En todos estos casos puede demostrarse que la corriente Ii que llega al electrodo i desde el exterior, es una combinación lineal de las tensiones a las que se encuentran los electrodos
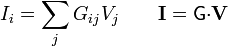
donde los Gij elementos de la matriz 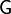 , son los llamados coeficientes de conductancia. Representan el análogo para corrientes de los coeficientes de capacidad para conductores en el vacío, y comparten muchas de sus propiedades (como el que forman una matriz simétrica, el que los elementos de la diagonal principal son positivos y el resto negativos o nulos).
, son los llamados coeficientes de conductancia. Representan el análogo para corrientes de los coeficientes de capacidad para conductores en el vacío, y comparten muchas de sus propiedades (como el que forman una matriz simétrica, el que los elementos de la diagonal principal son positivos y el resto negativos o nulos).
Si se fijan los voltajes de los distintos nodos mediante fuentes de tensión, es posible determinar las corrientes que fluyen hacia cada nodo. También es posible fijar las corrientes, mediante fuentes de intensidad, y hallar las tensiones. Como caso particular está el caso de electrodo que no está conectado a ninguna fuente. Esto equivale a que la intensidad que fluye hacia este nodo sea nula.
7.2 Circuitos equivalentes
A partir de los coeficientes de conductancia es posible construir un circuito equivalente formado por resistencias, de forma que la corriente que llega a un nodo se puede expresar como
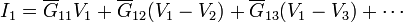
Este circuito contiene un nodo por cada electrodo. Entre cada dos nodos hay una conductancia overlineGij, y entre cada nodo y el electrodo de referencia (tierra) existe una conductancia adicional, 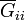 , de valores
, de valores
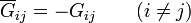
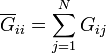
Aparte, deben añadirse las fuentes de tensión o de intensidad conectadas a cada nodo.
En términos del circuito equivalente, la ley de conservación de la carga en el estado estacionario se expresa como si tenemos un nodo (el “1”, por ejemplo) al cual no llega ningún aporte externo de corriente, se verifica que
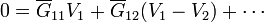
denotando por I1j la corriente que, en el circuito equivalente, fluye por la rama del nodo 1 al j (siendo j = 0 la tierra), nos queda
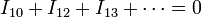
que es lo que se conoce habitualmente como ley de Kirchhoff para los nodos, aunque no tiene por qué aplicarse a un circuito formado por cables y conexiones puntuales.
8 Consumo de energía eléctrica
Cuando tenemos un conjunto de cargas en movimiento y un campo eléctrico actuando sobre ellas, este campo desarrolla una potencia
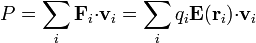
que, operando y pasando a una distribución continua, se transforma en
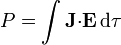
Esta potencia puede ser tanto positiva como negativa. En el primer caso el campo realiza trabajo, mientras que en el segundo absorbe energía.
En un medio óhmico, esta potencia siempre es positiva
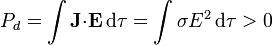
esta disipación de energía eléctrica se va en calor, denominándose efecto Joule.
También puede haber situaciones en el que la potencia sea positiva, pero no toda la energía se disipe en forma de calor. Es el caso de los motores, en los que energía eléctrica se transforma en energía mecánica.
En un generador, en el que la corriente, impulsada por el campo efectivo 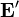 , va en sentido contrario al campo eléctrico, esta potencia es negativa
, va en sentido contrario al campo eléctrico, esta potencia es negativa
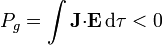
entendiéndose un generador como un dispositivo en el que energía mecánica, química o de otro tipo, se transforma en energía eléctrica.
Para el caso de un conductor filiforme el efecto Joule se puede expresar en términos de la corriente y la diferencia de potencial
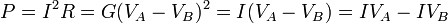
La última forma puede leerse como que la potencia consumida en el conductor es la diferencia entre la que se inyecta por el punto A y la que sale por el punto B.
En un sistema óhmico general, con N electrodos a distintos potenciales, la potencia eléctrica puede expresarse como
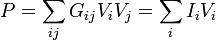
La primera de las formas nos da el consumo de energía en el interior del sistema, mientras que la segunda puede leerse como que este consumo equivale a la energía que entra por los terminales en la unidad de tiempo.
En términos del circuito equivalente, la potencia se escribe
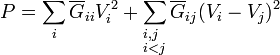
que se interpreta como que la potencia consumida es la suma de las que se disipan en cada una de las resistencias del circuito equivalente.
9 Fuerza electromotriz. Generadores
9.1 Generadores
Un generador es un dispositivo que puede producir una corriente eléctrica ejerciendo una fuerza no electrostática sobre las cargas eléctricas. Debe ser no electrostática pues un campo electrostático no puede producir trabajo neto sobre una curva cerrada y por tanto no puede mantener una corriente en un circuito cerrado. Como ejemplos de estas fuerzas tenemos fuerzas magnéticas, químicas o mecánicas, e incluso eléctricas (no estáticas).
Esta fuerza, que se representa por un campo efectivo 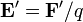 , mueve a las cargas situadas en el interior del generador, separándolas y creando la aparición de un polo positivo (o ánodo) y uno negativo (o cátodo).
, mueve a las cargas situadas en el interior del generador, separándolas y creando la aparición de un polo positivo (o ánodo) y uno negativo (o cátodo).
Esta separación de cargas provoca la aparición de un campo eléctrico, que irá de las cargas positivas a las negativas y tenderá a recombinarlas (actuando por tanto en contra del campo efectivo 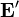 )).
)).
Cuando el sistema está en circuito abierto, esto es, no hay conexión exterior entre los polos del generador, las cargas son separadas por el campo efectivo hasta que se alcanza el equilibrio. Éste se produce cuando el campo eléctrico (que va creciendo a medida que se separan las cargas) compensa exactamente al efectivo. La corriente eléctrica a partir de ese momento es nula. Hay que destacar que, a diferencia del campo efectivo, el campo eléctrico existe tanto dentro como fuera del generador.
Si se cierra el circuito, conectando los polos mediante un material óhmico, las cargas tienen la posibilidad de recombinarse viajando por el exterior del generador y así lo hacen, impulsadas por el campo eléctrico exterior. Esto quiere decir que la carga acumulada en los polos es menor que en circuito abierto y el campo eléctrico en el interior del generador será menor que el campo efectivo. Por tanto, en el interior el campo efectivo produce una densidad de corriente en su misma dirección y sentido, cuya intensidad deberá ser igual a la que fluye de vuelta por el exterior.
9.2 Fuerza electromotriz
La acción neta de las fuerzas no electrostáticas que actúan en los generadores se mide con la fuerza electromotriz, cuya unidad es el voltio y definida como
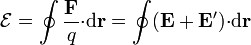
esto es, la integral a lo largo de una curva cerrada de la fuerza total por unidad de carga. Esta fuerza total incluye al campo electrostático  como al campo efectivo
como al campo efectivo 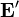 .
.
En circuito abierto, la fuerza electromotriz equivale a la diferencia de potencial entre bornes del generador
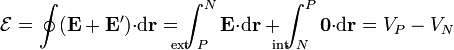
Cuando se establece la corriente, el campo no electrostático no sólo debe compensar al campo eléctrico, sino que debe devolver a las cargas, que han circulado por el exterior, a su electrodo original. Por ello, debe ser superior al campo eléctrico, ya que ha de superar la resistencia que opone el propio generador al movimiento de cargas por su interior, lo que se expresa a través de la relación
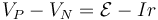
donde VP − VN es la diferencia de potencial entre bornes, I la corriente que atraviesa el generador y r la resistencia interna de éste.
Hay que remarcar que en el interior de un generador no se verifica la ley de Ohm, ya que la corriente o bien es nula o bien va en
sentido opuesto al campo eléctrico. En todo caso, se verifica 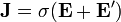 cuando el agente externo actúa en un medio óhmico.
cuando el agente externo actúa en un medio óhmico.
Modelando un generador real en un circuito equivalente, lo podemos considerar como compuesto de un generador ideal (sin resistencia interna) asociado en serie con una resistencia r.
Cuando se describe una curva cerrada en un sistema en estado estacionario, atravesando uno o varios generadores, la definición de fuerza electromotriz, trasladada al circuito equivalente, conduce a la ley de Kirchhoff para las mallas
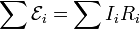
donde las Ii son las corrientes que circulan por las distintas ramas que recorremos, y las Ri incluyen también las resistencias internas de las fuentes.
10 Leyes de Kirchhoff
11 Corrientes no estacionarias
Cuando se tienen situaciones variables en el tiempo, las ecuaciones deben ampliarse para incluir la evolución de la densidad de carga
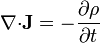
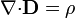

A este sistema hay que añadir las correspondientes condiciones de salto y de contorno, así como las relaciones constitutivas 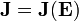 y
y 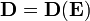 .
.
En un medio óhmico lineal se tiene
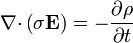
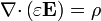

Si además el medio es homogéneo, estas ecuaciones pueden combinarse para obtener la ecuación de relajación de la carga
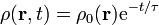
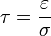
Esta ecuación establece que si en un punto de un material homogéneo la densidad de carga inicial es nula lo es en todo instante. Si hay una
densidad de carga inicial, ésta decrece exponencialmente, siendo el tiempo característico 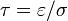 (tiempo de relajación de la carga) el parámetro que permite establecer si un material puede ser considerado como conductor casi perfecto, como buen dieléctrico, o se halla en una situación intermedia. Su valor puede ser desde nanosegundos o microsegundos (como es el caso del agua) hasta minutos o incluso horas.
(tiempo de relajación de la carga) el parámetro que permite establecer si un material puede ser considerado como conductor casi perfecto, como buen dieléctrico, o se halla en una situación intermedia. Su valor puede ser desde nanosegundos o microsegundos (como es el caso del agua) hasta minutos o incluso horas.
En un medio no homogéneo o con interfaces entre distintas regiones, puede producirse acumulación de carga en las superficies de separación, de acuerdo con las condiciones de salto
![\mathbf{n}{\cdot}[\mathbf{J}]=-\frac{\partial\sigma_s}{\partial t}](/wiki/images/math/8/3/b/83b04d3367bcca3153324d0378b69220.png)
![\nabla{\cdot}[\mathbf{D}]=\sigma](/wiki/images/math/8/9/7/897654a408a083b32b2a9698e1d92d88.png)
![\mathbf{n}\times[\mathbf{E}]=\mathbf{0}](/wiki/images/math/6/d/9/6d9a6f945a9f8273282ed8720257a0ba.png)
Otra situación variable en el tiempo de gran interés es el de la corriente alterna de baja frecuencia. Si en un conjunto de materiales lineales aplicamos tensiones que varían como cos(ωt), con ω pequeño, podemos seguir usando de forma aproximada las ecuaciones para corrientes estacionarias. En estas situaciones, tanto las corrientes como el campo eléctrico y las densidades de carga oscilan con la misma frecuencia que la tensión aplicada. Esto permite el uso de amplitudes complejas o fasores. Para una magnitud A
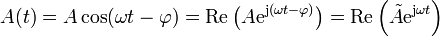
El fasor 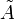 $ es un número complejo que incorpora tanto la amplitud de las oscilaciones como su desfase. En términos de las amplitudes complejas las ecuaciones diferenciales se convierten en ecuaciones algebraicas, lo que simplifica notablemente el cálculo. En particular, en numerosos sistemas, la relación entre la amplitud de la tensión aplicada y la corriente que fluye a un electrodo se puede expresar de forma sencilla como
$ es un número complejo que incorpora tanto la amplitud de las oscilaciones como su desfase. En términos de las amplitudes complejas las ecuaciones diferenciales se convierten en ecuaciones algebraicas, lo que simplifica notablemente el cálculo. En particular, en numerosos sistemas, la relación entre la amplitud de la tensión aplicada y la corriente que fluye a un electrodo se puede expresar de forma sencilla como
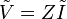
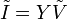
siendo Z e Y dos cantidades complejas (no oscilantes) conocidas como impedancia y admitancia}, respectivamente. Entre estos casos se cuenta una resistencia pura (para la cual Z = R) y un condensador ideal (para el cual Y = jωC).
El modelado de sistemas reales por circuitos equivalentes sometidos a corrientes alternas es mucho más complejo que en el caso estacionario, debido a los efectos de corrientes y acumulaciones localizadas de carga y de corrientes en el sistema. El caso más sencillo es el de un condensador de placas planas y paralelas, relleno de un material con pérdidas (caracterizado por  y σ). De la ecuación para la conservación de la carga en forma fasorial
y σ). De la ecuación para la conservación de la carga en forma fasorial
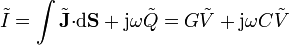
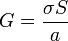
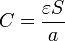
se deduce que puede ser modelado por un condensador y una conductancia puestos en paralelo
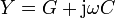
Sin embargo, para un sistema similar pero formado por dos capas de dieléctrico con pérdidas ya se requieren cuatro elementos de circuito. Normalmente es a la vista de la impedancia final como se construye el circuito, más que por simple inspección.
12 Corrientes de polarización
Un medio polarizado caracterizado por una polarización  , puede describirse de forma equivalente en términos de densidades de carga de volumen y de superficie
, puede describirse de forma equivalente en términos de densidades de carga de volumen y de superficie 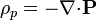 ,
, ![\sigma_p=-\mathbf{n}{\cdot}[\mathbf{P}]](/wiki/images/math/0/2/3/023b42905aa427503649d3765ab39002.png) , tal como se ve en tema de comportamiento dieléctrico de la materia. Si la polarización es dependiente del tiempo las cargas también lo serán. Para esta carga también se verifica una ley de conservación, por lo que asociada a esta variación debe haber una densidad de corriente (llamada corriente de polarización),
, tal como se ve en tema de comportamiento dieléctrico de la materia. Si la polarización es dependiente del tiempo las cargas también lo serán. Para esta carga también se verifica una ley de conservación, por lo que asociada a esta variación debe haber una densidad de corriente (llamada corriente de polarización), 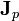 . Esta densidad viene dada por la expresión
. Esta densidad viene dada por la expresión
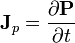
verificándose las leyes de conservación
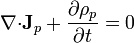
![\mathbf{n}{\cdot}[\mathbf{J}_p] = -\frac{\partial \sigma_p}{\partial t}](/wiki/images/math/f/b/6/fb6a82ec90b7fc5f6e1c067c012b4e6c.png)





