Ley de conservación de la carga
De Laplace
Contenido |
1 Enunciado
Una de las propiedades básicas de la interacción electromagnética es que la carga se conserva localmente, esto es, no puede crearse ni destruirse una carga neta en ningún punto.
2 Expresión matemática
Esto se traduce matemáticamente en que si en un volumen τ la carga contenida disminuye, ello se debe al flujo al exterior a través de la frontera:
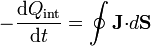
La versión diferencial de esta ley se escribe
Asociada a la ley de conservación de la carga existe una condición de salto que relaciona las densidades de corriente a ambos lados de una interfaz entre dos medios. Esta condición es, en general
![\mathbf{n}{\cdot}[\mathbf{J}] + \nabla_s{\cdot}\mathbf{K} + \frac{\partial\sigma_s}{\partial t}=0](/wiki/images/math/c/6/f/c6f6ea41accc6beef240415c3e40be5a.png)
siendo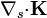 
la divergencia superficial de la densidad de corriente superficial. En muchos casos prácticos, no obstante, este término está ausente y la condición se reduce a una que liga el salto en 
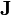con la variación de cargas en la superficie.
3 Corrientes estacionarias
En situaciones de corrientes estacionarias (independientes del tiempo), la densidad de corriente resulta ser un campo solenoidal
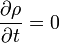
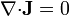
Esto implica que, para corrientes estacionarias, si consideramos un tubo de corriente, la intensidad en dos secciones cualesquiera de él es la misma
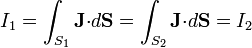
En situaciones no estacionarias esto no será cierto en general, ya que podrá haber acumulación de carga en los puntos intermedios.
En situaciones estacionarias la condición de salto (siempre que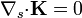 
) se reduce a
![\mathbf{n}{\cdot}[\mathbf{J}]=0](/wiki/images/math/a/d/6/ad621ced2218bcb1b784a17006bc2129.png)
esto es, que la corriente que llega normalmente a la superficie debe coincidir con la que sale de ella.
4 Aplicación a un electrodo
En el caso particular de un electrodo perfectamente conductor, sumergido en un material por el cual puede fluir una corriente 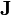, pero además alimentado por un cable (que lo une a un generador, por ejemplo), la ley de conservación de la carga puede desglosarse, separando la corriente que fluye por el medio, de la que entra hacia el electrodo por el cable de alimentación. Si denominamos I a esta última, la ley de conservación en forma integral queda
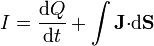
donde Q es la carga almacenada en el electrodo y el flujo de 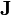se calcula a través del material que rodea al electrodo, excluyendo el cable. En esta forma, la ecuación se interpreta como que la corriente que llega al electrodo, parte se emplea en aumentar la carga almacenada y parte se escapa a través del medio circundante (lo que se denominan pérdidas). Nótese que sólo para esta clase de sistemas, y exclusivamente en el caso de que no haya pérdidas, se verificará la relación I = dQ / dt, que en ningún caso puede considerarse una definición de intensidad de corriente, sino sólo como un caso muy particular de la ley de conservación de la carga.
