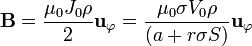Resistor conectado a generador real

De Laplace

Contenido

1 Enunciado
2 Campo y corriente
3 Potencia disipada
4 Energía almacenada
5 Campo magnético

1 Enunciado

El espacio entre dos placas conductoras circulares, planas y paralelas de radio $b$ , separadas una distancia $a$ , se encuentra lleno de un material de permitividad $\varepsilon$ , conductividad $σ$ y permeabilidad $μ 0$ . Las placas se encuentran conectadas a un generador real de f.e.m. $V 0$ y resistencia interna $r$ . En el estado estacionario, determine

La densidad de corriente y el campo eléctrico en el espacio entre las placas. Desprecie los efectos de borde.
La potencia total disipada en el volumen entre las placas. ¿Para qué valor de la conductividad es máxima esta potencia disipada?
La energía eléctrica almacenada en el material.
Sabiendo que el campo magnético entre las placas es acimutal y dependiente sólo de la distancia al eje, calcule el valor de este campo magnético.

2 Campo y corriente

Al ser las placas perfectamente conductoras y encontrarse el sistema en un estado estacionario, existe una diferencia de potencial constante entre las placas. Sea $Δ V$ esta d.d.p., considerando como placa a menor potencial la conectada al polo negativo de la fuente. Este voltaje no coincide con la f.e.m. de la fuente, debido a la caída de tensión en la resistencia interna. Se cumple que

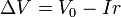
$\Delta V = V_0-I r\,$

y no conoceremos $Δ V$ hasta que hallemos la intensidad que circula por el sistema.

Suponiendo un valor dado para $Δ V$ (que hallaremos más tarde), el cálculo del campo eléctrico y la densidad de corriente es inmediato. Las ecuaciones que se cumplen son

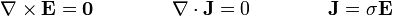
$\nabla\times\mathbf{E}=\mathbf{0}\qquad\qquad\nabla\cdot\mathbf{J}=0\qquad\qquad\mathbf{J}=\sigma\mathbf{E}$

Si despreciamos los efectos de borde y suponemos el campo con componente en la dirección normal a las placas

$\mathbf{E}=E\mathbf{u}_z\qquad\qquad\mathbf{J}=\sigma E\mathbf{u}_z$

Las ecuaciones anteriores conducen a que el campo eléctrico y la densidad de corriente son uniformes entre las placas.

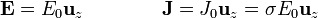
$\mathbf{E}=E_0\mathbf{u}_z\qquad\qquad\mathbf{J}=J_0\mathbf{u}_z=\sigma E_0\mathbf{u}_z$

El valor de la componente E_0 se relaciona con la d.d.p. a través de la relación

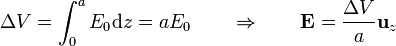
$\Delta V = \int_0^a E_0\mathrm{d}z=aE_0\qquad\Rightarrow\qquad \mathbf{E}=\frac{\Delta V}{a}\mathbf{u}_z$

A partir de la densidad de corriente hallamos la corriente que circula por el sistema, hallando su flujo a través de una sección transversal del material

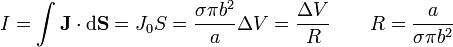
$I = \int \mathbf{J}\cdot\mathrm{d}\mathbf{S}=J_0 S = \frac{\sigma \pi b^2}{a}\Delta V = \frac{\Delta V}{R}\qquad R = \frac{a}{\sigma \pi b^2}$

Ahora que tenemos la relación entre la intensidad y el voltaje (que es simplemente la ley de Ohm), podemos hallar la d.d.p entre las placas:

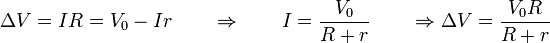
$\Delta V = IR = V_0 - Ir\qquad\Rightarrow\qquad I = \frac{V_0}{R+r}\qquad\Rightarrow\Delta V = \frac{V_0 R}{R+r}$

Vemos que el sistema no es más que un divisor de tensión.

A este resultado se podía haber llegado también mediante el circuito equivalente. Un condensador real equivale a una resistencia y condensador puestos en paralelo, con valores

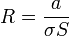
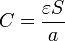
$R = \frac{a}{\sigma S}$ $C = \frac{\varepsilon S}{a}$

Esta asociación estaría en serie con la fuente y su resistencia interna. Al estar el sistema en corriente continua, por el condensador no pasa corriente y el circuito se reduce a dos resistencias en serie con la fuente.

Una vez que conocemos la d.d.p., podemos expresar el valor completo del campo eléctrico y la densidad de corriente

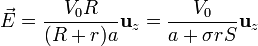
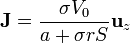
$\vec{E} = \frac{V_0 R}{(R+r)a}\mathbf{u}_z = \frac{V_0}{a+\sigma r S}\mathbf{u}_z$ $\mathbf{J}=\frac{\sigma V_0}{a+\sigma r S}\mathbf{u}_z$

3 Potencia disipada

La potencia disipada en el volumen la hallamos mediante la ley de Joule

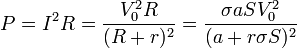
$P = I^2 R = \frac{V_0^2 R}{(R+r)^2} = \frac{\sigma a S V_0^2}{(a+r\sigma S)^2}$

Obtenemos el valor máximo de esta potencia, derivando respecto a la conductividad e igualando a 0

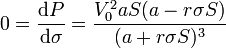
$0 = \frac{\mathrm{d}P}{\mathrm{d}\sigma} = \frac{V_0^2 a S(a-r\sigma S)}{(a+r \sigma S)^3}$

Esta derivada se anula para

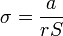
$\sigma = \frac{a}{r S}$

siendo el valor de la potencia máxima disipada

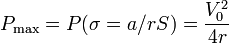
$P_\mathrm{max} = P(\sigma = a/rS) = \frac{V_0^2}{4r}$

Vemos que la potencia máxima no se da para $σ = 0$ (cuando el medio es perfectamente dieléctrico y no hay corriente en él) ni para 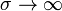$\sigma\to\infty$ (en el que se hace perfectamente conductor y el campo eléctrico en su interior se anula), sino en un valor intermedio de la conductividad.

Alternativamente, puede hacerse el cálculo en términos de la resistencia del elemento

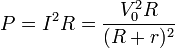
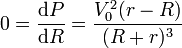
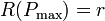
$P = I^2 R = \frac{V_0^2R}{(R+r)^2}$ $0 = \frac{\mathrm{d}P}{\mathrm{d}R}= \frac{V_0^2(r-R)}{(R+r)^3}$ $\Rightarrow$ $R(P_\mathrm{max})=r\,$

La potencia disipada en el material es máxima cuando la resistencia del bloque es igual a la interna de la fuente $R = r$ (lo cual constituye otro resultado conocido de teoría de circuitos).

Alternativamente, podemos deducirlo observando que

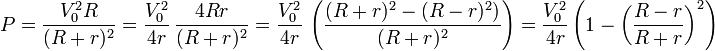
$P = \frac{V_0^2R}{(R+r)^2} = \frac{V_0^2}{4r}\,\frac{4Rr}{(R+r)^2} = \frac{V_0^2}{4r}\,\left(\frac{(R+r)^2-(R-r)^2)}{(R+r)^2}\right)=\frac{V_0^2}{4r}\left(1-\left(\frac{R-r}{R+r}\right)^2\right)$

y puesto que se trata el término que se resta es positivo y todo lo demás independiente de $R$ , el valor máximo de la potencia se da cuando este término se anule, esto es, cuando $R = r$ . Además obtenemos el valor máximo de la potencia disipada

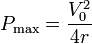
$P_\mathrm{max}=\frac{V_0^2}{4r}$

4 Energía almacenada

La energía almacenada en el espacio entre las placas, es inmediata a partir del campo eléctrico

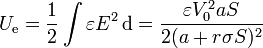
$U_\mathrm{e}=\frac{1}{2}\int \varepsilon E^2\,\mathrm{d} = \frac{\varepsilon V_0^2 a S}{2(a+r\sigma S)^2}$

Alternativamente, puede hallarse a partir de la energía almacenada en un condensador

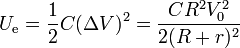
$U_\mathrm{e}=\frac{1}{2}C(\Delta V)^2 = \frac{CR^2V_0^2}{2(R+r)^2}$

5 Campo magnético

Puesto que se nos dice que el campo es acimutal y dependiente solo de la distancia al eje

$\mathbf{B}=B(\rho)\mathbf{u}_\varphi$

podemos hallar el campo magnético por simple aplicación de la ley de Ampère. Considerando una circunferencia horizontal de radio $ρ$ resulta la circulación

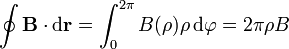
$\oint \mathbf{B}\cdot\mathrm{d}\mathbf{r}=\int_0^{2\pi} B(\rho)\rho\,\mathrm{d}\varphi=2\pi\rho B$

y, según la ley de Ampère, debe ser igual a la corriente que atraviesa una superficie apoyada en la circunferencia, multiplicada por $μ 0$

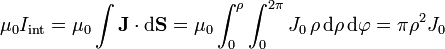
$\mu_0I_\mathrm{int}=\mu_0\int\mathbf{J}\cdot\mathrm{d}\mathbf{S}=\mu_0\int_0^\rho\int_0^{2\pi} J_0\,\rho\,\mathrm{d}\rho\,\mathrm{d}\varphi=\pi\rho^2 J_0$

Igualando y despejando

$\mathbf{B}=\frac{\mu_0J_0\rho}{2}\mathbf{u}_\varphi=\frac{\mu_0\sigma V_0\rho}{(a+r\sigma S)}\mathbf{u}_\varphi$

Resistor conectado a generador real

De Laplace

Contenido

1 Enunciado

2 Campo y corriente

3 Potencia disipada

4 Energía almacenada

5 Campo magnético

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES