Campos en un condensador sometido a un voltaje alterno
De Laplace
1 Enunciado
Suponga que se sumergen dos conductores perfectos en un material de permitividad  y conductividad σ. Si se aplica entre ellos una diferencia de potencial constante V0 la corriente que llega a uno de ellos vale I0. ¿Cuál será la corriente si el voltaje varía como
y conductividad σ. Si se aplica entre ellos una diferencia de potencial constante V0 la corriente que llega a uno de ellos vale I0. ¿Cuál será la corriente si el voltaje varía como 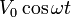 ?
?
2 Solución
Cuando el estado no es estacionario, es necesario considerar las variaciones de carga en los conductores. En este caso, la corriente que llega a los conductores por los cables, no coincide en general con la que atraviesa el medio. Como en otros problemas, denominaremos I1 e I2 las corrientes que llegan a cada conductor (aunque una de las dos sea negativa, indicando con ello que en realidad sale).
Si calculamos el flujo de la densidad de corriente a través de una superficie cerrada que, por el interior del material óhmico, envuelva al conductor 1, tenemos, según la ley de conservación de la carga
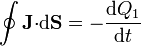
La integral de superficie se compone de una parte a través del cable, más una a través del material óhmico
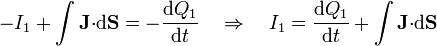
Según esto, de la corriente que llega por el cable, una parte (la llamada componente capacitiva) se emplea en variar la carga almacenada en el conductor, y otra (llamada componente resistiva) fluye a través del material óhmico.
En el caso estacionario el primer término no aparece y la expresión se reduce a
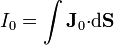
Esta corriente es proporcional a la diferencia de potencial entre los conductores, siendo la constante de proporcionalidad la conductancia
lo que equivale a definir la conductancia como
Si tenemos variación en la carga almacenada debemos añadir el término
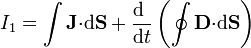
Si admitimos que la distribución de los campos es la misma tanto si estamos en corriente continua como en alterna de baja frecuencia, el primer término sigue valiendo

mientras que el segundo se relaciona con el primero, ya que la carga depende de la diferencia de potencial a través de la capacidad
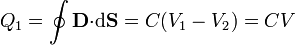
Si el material intermedio es homogéneo y despreciamos la pequeña contribución a la carga correspondiente a la sección del cable, la capacidad y la conductancia están relacionadas como
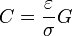
y la ecuación para la corriente se convierte en
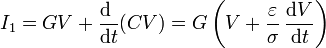
lo que se puede representar, en un circuito equivalente, como una capacidad y una conductancia puestas en paralelo (ya que la tensión es la misma y las corrientes se suman).
Para el caso de una tensión sinusoidal, esta expresión se convierte en
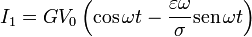
Sabemos que, en el estado estacionario, I0 = GV0, por lo que el resultado final para la corriente es
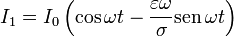
Cuando la dependencia temporal es sinusoidal, es conveniente el empleo de fasores. Para ello, se puede hacer uso, para todas las magnitudes oscilantes, de la fórmula de Euler y escribir
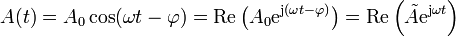
donde hemos introducido la amplitud compleja o fasor de A.
Si en lugar de las funciones dependientes del tiempo empleamos sus amplitudes complejas, la corriente total queda
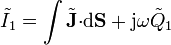
y, al sustituir,
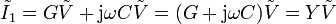
La cantidad compleja (pero no oscilante) Y recibe el nombre de admitancia del sistema. Su inversa, de uso más común, se conoce como impedancia
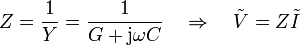
Las reglas para el manejo de impedancias son análogas a las de las resistencias. En particular, en este caso tenemos que la impedancia corresponde a la asociación en paralelo de una resistencia y de un condensador.
Teniendo en cuenta la relación entre capacidad y conductancia queda, para la corriente

donde 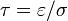 , es el tiempo de relajación de la carga en el material.
, es el tiempo de relajación de la carga en el material.
Para ver cual de los dos factores, el resistivo o el capacitivo, es más importante, debemos comparar la cantidad $\omega\tau$ frente a la unidad. Equivalentemente, si tenemos en cuenta que ω = 2π / T (con T el periodo de la oscilación, el criterio de importancia es que si

Si el tiempo de relajación es mucho más corto que el periodo, a las cargas les da tiempo de llegar casi al estado estacionario y la componente resistiva es más importante que la capacitiva. Por el contrario, si
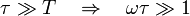
Si el tiempo de relajación es muy largo (lo que ocurre para un dieléctrico muy bueno) o la frecuencia es alta, el término capacitivo es dominante.
Este problema es aproximado por varias razones. Primero, porque al no ser estacionario, las leyes de la electrostática son solo aproximadas y un cálculo exacto requeriría la inclusión de fenómenos inductivos de origen electromagnético. Estos efectos suelen ser muy pequeños, salvo a frecuencias muy altas, por lo que es bastante seguro prescindir de ellos en un circuito formado por resistencias y condensadores a baja frecuencia.
Una segunda causa, de mayor importancia práctica, es la hipótesis de que las distribuciones de los campos son las mismas en el estado estacionario que en el oscilatorio. Esta hipótesis falla cuando existe acumulación de carga en otras partes del sistema. Puede acumularse carga:
- en el material óhmico, si este no es homogéneo,
- en las interfaces, si está formado por varios materiales diferentes,
- en la superficie exterior del medio, lindando con el vacío.
El primer caso no es frecuente, pero el segundo sí puede aparecer y el tercero ocurre siempre. Supongamos dos electrodos conectados por un cable. Al establecer una tensión, aparecen cargas en la superficie del cable que son las que desvían las líneas de corriente y hacen que sigan el trazado del cable. Durante el transitorio inicial, la corriente que entra por un electrodo no coincide con la que sale por el otro, debido a la acumulación de carga en otras partes del sistema. Durante este transitorio, las líneas de corriente no son tangentes a la superficie, sino que tendrán una cierta corriente normal a ella.
Para modelar esta comportamiento puede construirse un circuito equivalente que incluye otros condensadores y resistencias (denominados parásitos) para representar estas acumulaciones de carga.
Lo que ocurre es que, en la mayoría de los casos reales, estas capacidades suelen ser absolutamente minúsculas, y por ello, no se comete un gran error al despreciarlas.
Una consecuencia adicional es que la capacidad no es la misma en el estado estacionario que en una situación variable, ya que al ser diferentes las distribuciones de los campos, también lo es la carga acumulada en cada conductor. Este efecto, también se puede representar introduciendo nuevas capacidades parásitas, despreciables a bajas frecuencias.
Hay casos en los que no se pueden despreciar. Por ejemplo, en el problema del condensador relleno parcialmente se trata una situación en la que se tienen dos electrodos separados por dos materiales con una interfaz entre ellos. En este caso, la acumulación de carga en esta superficie obliga a complicar el circuito, introduciendo tres elementos, en lugar de dos.





